Необходимый и достаточные признаки сходимости.

ВВЕДЕНИЕ

Методическое пособие предназначено для преподавателей математики в техникумах, а также для студентов второго курса, всех специальностей.

В данной работе излагаются основные понятия теории рядов. Теоретический материал соответствует требованиям Государственного образовательного стандарта среднего профессионального образования (Министерство образования Российской Федерации. М., 2002г.).

Изложение теоретического материала по всей теме сопровождается рассмотрением большого количества примеров и задач, ведется на доступном, по-возможности строгом языке. В конце пособия приведены примеры и задания, которые студенты могут выполнять в режиме самоконтроля.

Пособие предназначено для студентов заочной и дневной форм обучения.

Учитывая уровень подготовки учащихся техникума, а также крайне ограниченное число часов (12 часов + 4 ф.), отводимое программой для прохождения высшей математики в техникумах, строгие выводы, представляющие большие трудности для усвоения, опущены, ограничиваясь рассмотрением примеров.

ОСНОВНЫЕ ПОНЯТИЯ

Решение задачи, представленной в математических терминах, например, в виде комбинации различных функций, их производных и интегралов, нужно уметь “довести до числа”, которое чаще всего и служит окончательным ответом. Для этого в различных разделах математики выработаны различные методы.

Раздел математики, позволяющий решить любую корректно поставленную задачу с достаточной для практического использования точностью, называется теорией рядов.

Даже если некоторые тонкие понятия математического анализа появились вне связи с теорией рядов, они немедленно применялись к рядам, которые служили как бы инструментом для испытания значимости этих понятий. Такое положение сохраняется и сейчас.

Выражение вида

,

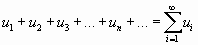где 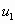; ; 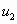;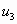…; ;… 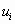- члены ряда; 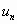- n-ый или общий член ряда, называется бесконечным рядом (рядом).

Если члены ряда :

• числа, то ряд называется числовым;
• числа одного знака, то ряд называется знакопостоянным;
• числа разных знаков, то ряд называется знакопеременным;
• положительные числа, то ряд называется знакоположительным;
• числа, знаки которых строго чередуются, то ряд называется знакочередующимся;
• функции, то ряд называется функциональным;
• степени 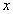, то ряд называется степенным;
• тригонометрические функции, то ряд называется тригонометрическим.

I. Числовой ряд

Основные понятия числового ряда.

Числовым рядом называется сумма вида

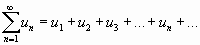, (1.1)

где 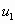, , 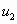,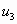…, ,…, 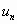называемые членами ряда, образуют бесконечную последовательность; член 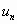называется общим членом ряда.

Суммы

…………..

,

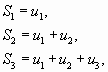
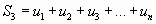составленные из первых членов ряда (1.1), называются частичными суммами этого ряда.

Каждому ряду можно сопоставить последовательность частичных сумм .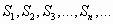

Если при бесконечном возрастании номера n частичная сумма ряда 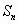стремится к пределу 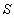, то ряд называется сходящимся, а число 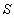- суммой сходящегося ряда, т.е.

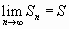и .

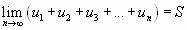Эта запись равносильна записи

.

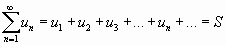Если частичная сумма 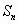ряда (1.1) при неограниченном возрастании n не имеет конечного предела (стремится к 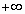или 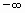), то такой ряд называется расходящимся.

Если ряд сходящийся, то значение 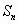при достаточно большом n является приближенным выражением суммы ряда S.

Разность 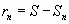называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е. 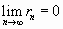, и наоборот, если остаток стремится к нулю, то ряд сходится.

Примеры числовых рядов.

Пример 1. Ряд вида

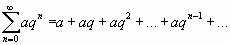(1.2)

называется геометрическим .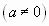

Геометрический ряд образован из членов геометрической прогрессии.

Известно, что сумма её первых n членов 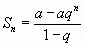. Очевидно: это n-ая частичная сумма ряда (1.2).

Возможны случаи:

:

.

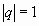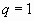Ряд (1.2) принимает вид:

,

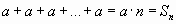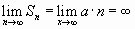,ряд расходится;

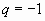
Ряд (1.2) принимает вид:

,

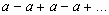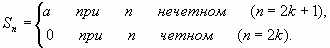
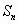не имеет предела, ряд расходится.

,

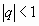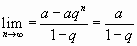- конечное число, ряд сходится.

,

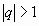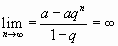- ряд расходится.

Итак, данный ряд сходится при 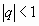и расходится при .

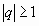Пример 2. Ряд вида

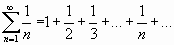(1.3)

называется гармоническим.

Запишем частичную сумму этого ряда:

.

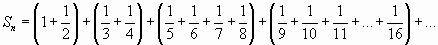Сумма 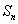больше суммы, представленной следующим образом:

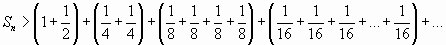
или .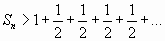

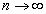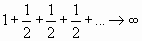Если , то , или .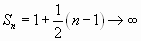

Следовательно, если 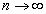, то 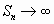, т.е. гармонический ряд расходится.

Пример 3. Ряд вида

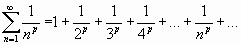(1.4)

называется обобщенным гармоническим.

Если 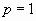, то данный ряд обращается в гармонический ряд, который является расходящимся.

Если 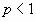, то члены данного ряда больше соответствующих членов гармонического ряда и, значит, он расходится. При 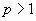имеем геометрический ряд, в котором 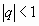; он является сходящимся.

Итак, обобщенный гармонический ряд сходится при 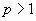и расходится при .

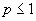Признак Даламбера.

Если для ряда с положительными членами

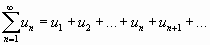
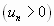
выполняется условие 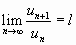, то ряд сходится при 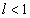и расходится при .

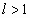Признак Даламбера не дает ответа, если 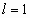. В этом случае для исследования ряда применяются другие приемы.

Упражнения.

Записать ряд по его заданному общему члену:

;

;

.

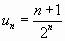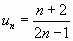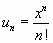Решение.

Полагая 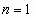, , 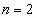,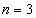…, имеем бесконечную последовательность чисел:

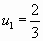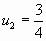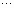, , . Сложив его члены, получим ряд

.

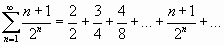Поступая так же, получим ряд

.

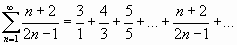Придавая 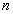значения 1,2,3,… и учитывая, что 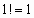, , 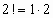,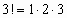…, получим ряд

.

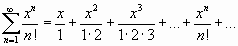Найти n-ый член ряда по его данным первым членам:

;

.

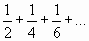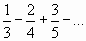Решение.

Знаменатели членов ряда, начиная с первого, являются четными числами; следовательно, n-ый член ряда имеет вид .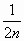

Числители членов ряда образуют натуральный ряд чисел, а соответствующие им знаменатели – натуральный ряд чисел, а соответствующие им знаменатели – натуральный ряд чисел, начиная с 3. Знаки чередуются по закону 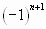или по закону 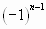. Значит, n-й член ряда имеет вид 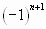. 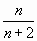или .

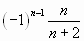Исследовать сходимость ряда, применяя необходимый признак сходимости и признак сравнения:

;

;

.

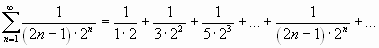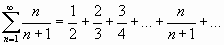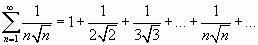Решение.

Находим .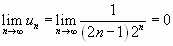

Необходимый признак сходимости ряда выполняется, но для решения вопроса о сходимости нужно применить один из достаточных признаков сходимости. Сравним данный ряд с геометрическим рядом

,

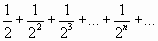который сходится, так как .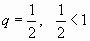

Сравнивая члены данного ряда, начиная со второго, с соответствующими членами геометрического ряда, получим неравенства

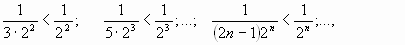
т.е. члены данного ряда, начиная со второго, соответственно меньше членов геометрического ряда, откуда следует, что данный ряд сходится.

Имеем

.

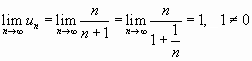Здесь выполняется достаточный признак расходимости ряда; следовательно, ряд расходится.

Находим .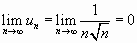

Необходимый признак сходимости ряда выполняется. Сравним данный ряд с обобщенным гармоническим рядом

,

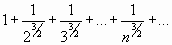который сходится, поскольку 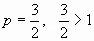, следовательно, сходится и данный ряд.

Исследовать сходимость ряда, используя признак Даламбера:

;

.

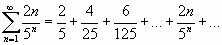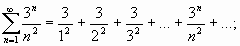
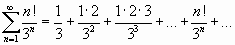Решение.

Подставив в общий член ряда 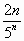вместо n число n+1, получим 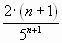. Найдем предел отношения 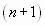-го члена к n-му члену при :

.

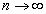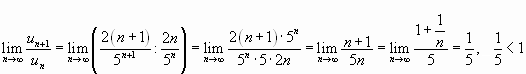Следовательно, данный ряд сходится.

Имеем

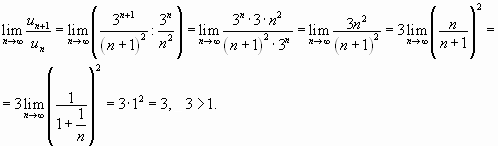
Значит, данный ряд расходится.

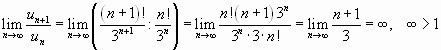, т.е. ряд расходится.

II. Знакопеременный ряд

Замечания.

Исследование знакочередующегося ряда вида

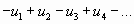
(с отрицательным первым членом) сводится путем умножения всех его членов на 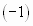к исследованию ряда .

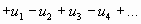Ряды, для которых выполняются условия теоремы Лейбница, называются лейбницевскими (или рядами Лейбница).

Соотношение 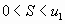позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму S данного ряда его частичной суммой .

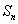Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд 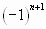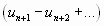, сумма которого по модулю меньше первого члена этого ряда, т.е. 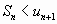. Поэтому ошибка меньше модуля первого из отброшенных членов.

Пример. Вычислить приблизительно сумму ряда .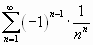

Решение: данный ряд Лейбницевского типа. Он сходится. Можно записать:

.

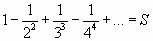Взяв пять членов, т.е. заменив 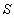на

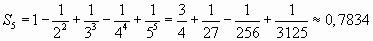, сделаем ошибку, меньшую,

чем 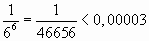. Итак, .

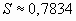Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.

Теорема. Пусть дан знакопеременный ряд

.

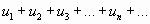Если сходится ряд

,

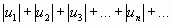составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.

Признак сходимости Лейбница для знакочередующихся рядов служит достаточным признаком сходимости знакочередующихся рядов.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов, т.е. всякий абсолютно сходящийся ряд является сходящимся.

Если знакопеременный ряд сходится, а составленный из абсолютных величин его членов ряд расходится, то данный ряд называется условно (неабсолютно) сходящимся.

Упражнения.

Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:

;

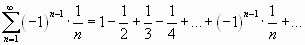Решение.

Члены данного ряда по абсолютной величине монотонно убывают:

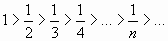и

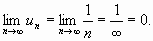
Следовательно, согласно признаку Лейбница, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.

Ряд 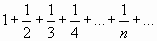, составленный из абсолютных величин данного ряда, является гармоническим рядом, который, расходится. Поэтому данный ряд сходится условно.

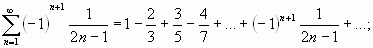
Решение.

Члены данного ряда по абсолютной величине монотонно убывают:

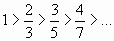, но

.

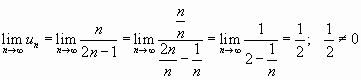Ряд расходится, так как признак Лейбница не выполняется.

;

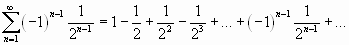Решение.

Используя признак Лейбница, получим

; ,

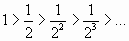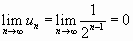т.е. ряд сходится.

Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:

.

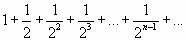Это геометрический ряд вида 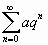, где 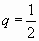, который сходится. Поэтому данный ряд сходится абсолютно.

;

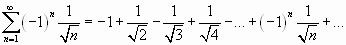Решение.

Используя признак Лейбница, имеем

;

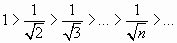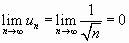, т.е. ряд сходится.

Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:

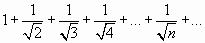, или

.

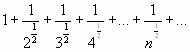Это обобщенный гармонический ряд, который расходится, так как 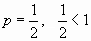. Следовательно, данный ряд сходится условно.

III. Функциональный ряд

Степенные ряды.

Степенным рядом называется ряд вида

,

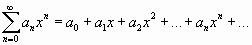где числа 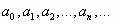называются коэффициентами ряда, а член 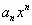- общим членом ряда.

Областью сходимости степенного ряда называется множество всех значений 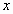, при которых данный ряд сходится.

Число 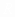называется радиусом сходимости степенного ряда, если при 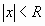ряд сходится и притом абсолютно, а при 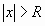ряд расходится.

Радиус сходимости 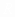найдем, используя признак Даламбера:

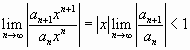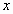( не зависит от ),

,

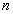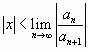т.е. если степенной ряд сходится при любых 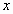, удовлетворяющих данному условию и расходится при .

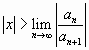Отсюда следует, что если существует предел

,

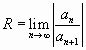
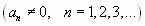то радиус сходимости ряда 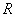равен этому пределу и степенной ряд сходится при 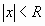, т.е. в промежутке 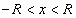, который называется промежутком (интервалом) сходимости.

Если 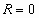, то степенной ряд сходится в единственной точке .

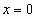На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходиться.

Сходимость степенного ряда пр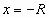и и 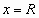исследуется с помощью какого-либо из признаков сходимости.

Упражнения.

Найти область сходимости ряда:

;

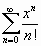Решение. Найдем радиус сходимости данного ряда:

.

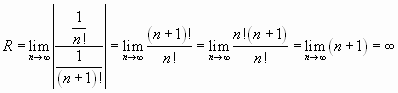Следовательно, данный ряд абсолютно сходится на всей числовой оси.

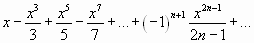
Решение. Воспользуемся признаком Даламбера. Для данного ряда имеем:

, ,

.

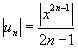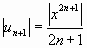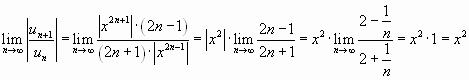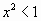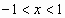Ряд абсолютно сходится, если или . Исследуем поведение ряда на концах интервала сходимости.

При 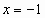имеем ряд 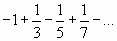, который сходится по признаку Лейбница.

При 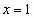имеем ряд 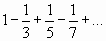- это тоже сходящийся Лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок .

.

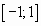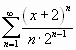Решение. Найдем радиус сходимости ряда:

.

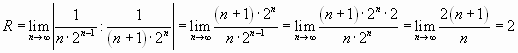Следовательно, ряд сходится при 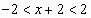, т.е. при .

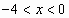При 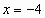имеем ряд 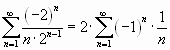, который сходится по признаку Лейбница.

При 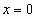имеем расходящийся ряд

.

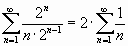Следовательно, областью сходимости исходного ряда является промежуток .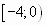

VI. Ответы

I.

1. сходится;
2. расходится;
3. сходится;
4. сходится;
5. расходится;
6. сходится;
7. сходится;
8. расходится;
9. сходится;
10. сходится.

II.

1. cходится абсолютно;
2. cходится абсолютно;
3. cходится условно;
4. cходится условно;
5. cходится абсолютно.

III.

1. ;
2. ;
3. ;
4. ;
5. .

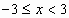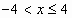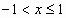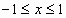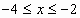IV.

;

;

;

;

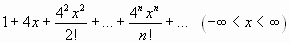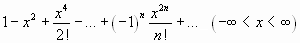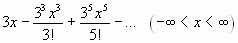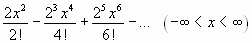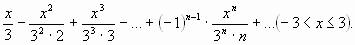
VII. Историческая справка.

Решение многих задач сводится к вычислению значений функций и интегралов или к решению дифференциальных уравнений, содержащих производные или дифференциалы неизвестных функций.

Однако точное выполнение указанных математических операций во многих случаях оказывается весьма затруднительным или невозможным. В этих случаях можно получить приближенное решение многих задач с любой желаемой точностью при помощи рядов.

Ряды представляют собой простой и совершенный инструмент математического анализа для приближенного вычисления функций, интегралов и решений дифференциальных уравнений.

Теория рядов создавалась в тесной связи с теорией приближенного представления функций в виде многочленов. Впервые это сделал И. Ньютон (1642 – 1727). в 1676г. В его письме к секретарю Лондонского Королевского Общества появилась формула:

,

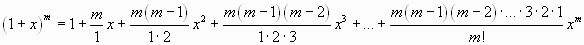которую мы знаем как формулу бинома Ньютона.

Здесь мы видим функцию 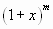, представленную в виде многочлена. Но если число 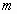не является натуральным, в правой части равенства получается не полином, а бесконечная сумма слагаемых, то есть ряд.

Развивая идею Ньютона, английский математик Брук Тейлор (1685 – 1731) в 1715г. доказал, что любой функции, имеющей в точке 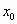производные всех порядков, можно сопоставить ряд:

.

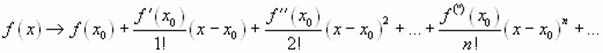Мы не можем пока поставить знак равенства между функцией 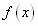, принимающей конечное значение для любого значения 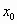, и стоящим справа функциональным рядом.

Для того, чтобы вместо знака “ 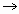” можно было поставить знак равенства, необходимо провести некоторые дополнительные рассуждения, связанные именно с бесконечностью числа слагаемых в правой части равенства и касающиеся области сходимости ряда.

При 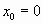формула Тейлора принимает вид, в котором называется формулой Маклорена:

.

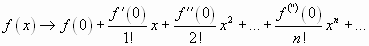Колин Маклорен (1698 – 1746), ученик Ньютона, в работе “Трактат о флюксиях” (1742) установил, что степенной ряд, выражающий аналитическую функцию, - единственный, и это будет ряд Тейлора, порожденный такой функцией. В формуле бинома Ньютона коэффициенты при степенях 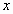представляют собой значения 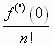, где .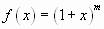

Итак, ряды возникли в XVIII в. как способ представления функций, допускающих бесконечное дифференцирование. Однако функция, представляемая рядом, не называлась его суммой, и вообще в то время не было еще определено, что такое сумма числового или функционального ряда, были только попытки ввести это понятие.

Например, Л. Эйлер (1707-1783), выписав для функции соответствующий ей степенной ряд, придавал переменной 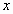конкретное значение 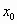. Получался числовой ряд. Суммой этого ряда Эйлер cчитал значение исходной функции в точке 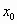. Но это не всегда верно.

О том, что расходящийся ряд не имеет суммы, ученые стали догадываться только в XIX в., хотя в XVIII в. многие, и прежде всего Л. Эйлер, много работали над понятиями сходимости и расходимости. Эйлер называл ряд 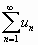сходящимся, если его общий член 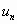стремится к нулю при возрастании .

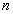В теории расходящихся рядов Эйлер получил немало существенных результатов, однако результаты эти долго не находили применения. Еще в 1826г. Н.Г. Абель (1802 – 1829) называл расходящиеся ряды “дьявольским измышлением”. Результаты Эйлера нашли обоснование лишь в конце XIX в.

В формировании понятия суммы сходящегося ряда большую роль сыграл французский ученый О.Л. Коши (1789 – 1857); он сделал чрезвычайно много не только в теории рядов, но и теории пределов, в разработке самого понятия предела. В 1826г. Коши заявил, что расходящийся ряд не имеет суммы.

В 1768г. французский математик и философ Ж.Л. Д’Аламбер исследовал отношение последующего члена к предыдущему в биномиальном ряде и показал, что если это отношение по модулю меньше единицы, то ряд сходится. Коши в 1821г. доказал теорему, излагающую в общем виде признак сходимости знакоположительных рядов, называемых теперь признаком Д’Аламбера.

Для исследования сходимости знакочередующихся рядов используется признак Лейбница.

Г.В. Лейбниц (1646 – 1716), великий немецкий математик и философ, наряду с И. Ньютоном является основоположником дифференциального и интегрального исчисления.

Список литературы:

Основная:

1. Богомолов Н.В., Практические занятия по математике. М., “Высшая школа”, 1990 – 495 с.;
2. Тарасов Н.П., Курс высшей математики для техникумов. М., “Наука”, 1971 – 448 с.;
3. Зайцев И.Л., Курс высшей математики для техникумов. М., государственное издательство техникумов – теоретической литературы, 1957 - 339 с.;
4. Письменный Д.Т., Курс лекций по высшей математике. М., “Айрис Пресс”, 2005, часть 2 – 256 с.;
5. Выгодский М.Я., Справочник по высшей математике. М., “Наука”, 1975 – 872 с.;

ВВЕДЕНИЕ

Методическое пособие предназначено для преподавателей математики в техникумах, а также для студентов второго курса, всех специальностей.

В данной работе излагаются основные понятия теории рядов. Теоретический материал соответствует требованиям Государственного образовательного стандарта среднего профессионального образования (Министерство образования Российской Федерации. М., 2002г.).

Изложение теоретического материала по всей теме сопровождается рассмотрением большого количества примеров и задач, ведется на доступном, по-возможности строгом языке. В конце пособия приведены примеры и задания, которые студенты могут выполнять в режиме самоконтроля.

Пособие предназначено для студентов заочной и дневной форм обучения.

Учитывая уровень подготовки учащихся техникума, а также крайне ограниченное число часов (12 часов + 4 ф.), отводимое программой для прохождения высшей математики в техникумах, строгие выводы, представляющие большие трудности для усвоения, опущены, ограничиваясь рассмотрением примеров.

ОСНОВНЫЕ ПОНЯТИЯ

Решение задачи, представленной в математических терминах, например, в виде комбинации различных функций, их производных и интегралов, нужно уметь “довести до числа”, которое чаще всего и служит окончательным ответом. Для этого в различных разделах математики выработаны различные методы.

Раздел математики, позволяющий решить любую корректно поставленную задачу с достаточной для практического использования точностью, называется теорией рядов.

Даже если некоторые тонкие понятия математического анализа появились вне связи с теорией рядов, они немедленно применялись к рядам, которые служили как бы инструментом для испытания значимости этих понятий. Такое положение сохраняется и сейчас.

Выражение вида

,

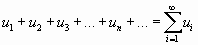где 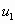; ; 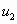;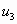…; ;… 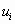- члены ряда; 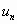- n-ый или общий член ряда, называется бесконечным рядом (рядом).

Если члены ряда :

• числа, то ряд называется числовым;
• числа одного знака, то ряд называется знакопостоянным;
• числа разных знаков, то ряд называется знакопеременным;
• положительные числа, то ряд называется знакоположительным;
• числа, знаки которых строго чередуются, то ряд называется знакочередующимся;
• функции, то ряд называется функциональным;
• степени 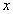, то ряд называется степенным;
• тригонометрические функции, то ряд называется тригонометрическим.

I. Числовой ряд

Основные понятия числового ряда.

Числовым рядом называется сумма вида

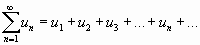, (1.1)

где 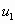, , 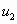,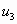…, ,…, 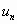называемые членами ряда, образуют бесконечную последовательность; член 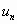называется общим членом ряда.

Суммы

…………..

,

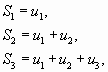
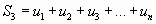составленные из первых членов ряда (1.1), называются частичными суммами этого ряда.

Каждому ряду можно сопоставить последовательность частичных сумм .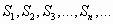

Если при бесконечном возрастании номера n частичная сумма ряда 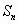стремится к пределу 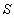, то ряд называется сходящимся, а число 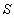- суммой сходящегося ряда, т.е.

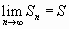и .

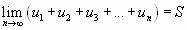Эта запись равносильна записи

.

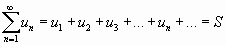Если частичная сумма 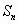ряда (1.1) при неограниченном возрастании n не имеет конечного предела (стремится к 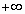или 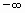), то такой ряд называется расходящимся.

Если ряд сходящийся, то значение 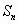при достаточно большом n является приближенным выражением суммы ряда S.

Разность 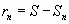называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е. 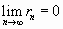, и наоборот, если остаток стремится к нулю, то ряд сходится.

Примеры числовых рядов.

Пример 1. Ряд вида

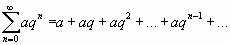(1.2)

называется геометрическим .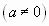

Геометрический ряд образован из членов геометрической прогрессии.

Известно, что сумма её первых n членов 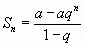. Очевидно: это n-ая частичная сумма ряда (1.2).

Возможны случаи:

:

.

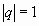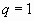Ряд (1.2) принимает вид:

,

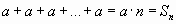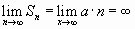,ряд расходится;

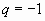
Ряд (1.2) принимает вид:

,

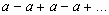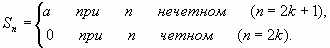
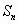не имеет предела, ряд расходится.

,

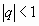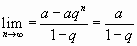- конечное число, ряд сходится.

,

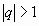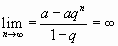- ряд расходится.

Итак, данный ряд сходится при 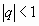и расходится при .

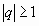Пример 2. Ряд вида

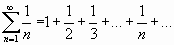(1.3)

называется гармоническим.

Запишем частичную сумму этого ряда:

.

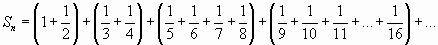Сумма 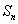больше суммы, представленной следующим образом:

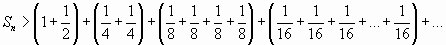
или .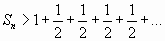

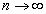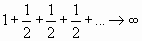Если , то , или .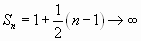

Следовательно, если 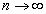, то 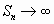, т.е. гармонический ряд расходится.

Пример 3. Ряд вида

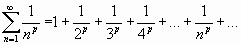(1.4)

называется обобщенным гармоническим.

Если 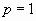, то данный ряд обращается в гармонический ряд, который является расходящимся.

Если 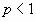, то члены данного ряда больше соответствующих членов гармонического ряда и, значит, он расходится. При 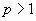имеем геометрический ряд, в котором 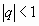; он является сходящимся.

Итак, обобщенный гармонический ряд сходится при 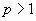и расходится при .

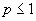Необходимый и достаточные признаки сходимости.

Необходимый признак сходимости ряда.

Ряд 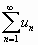может сходиться только при условии, что его общий член 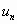при неограниченном увеличении номера