Метод подстановкив неопределенном интеграле

(метод замены переменной)

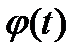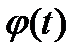Этот метод заключается в том, что заменяют переменную х на ,где -непрерывно дифференцируемая функция, полагают 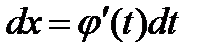и получают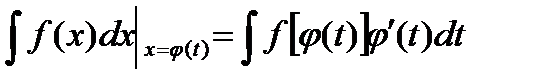

При этом получают искомую функцию, выраженную через переменную t. Для возвращения к переменной х необходимо заменить t значением 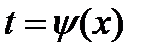, которое находится из соотношения .

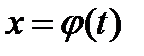Рассмотрим нахождение интегралов методом подстановки.

Пример 1: Найти неопределенный интеграл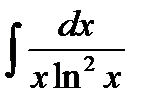

Решение: =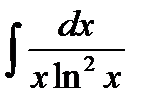

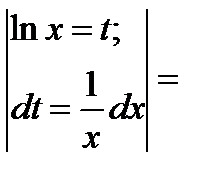
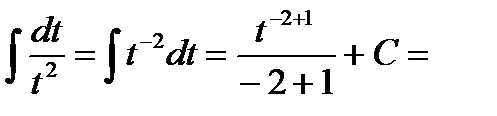
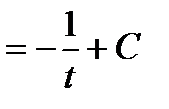
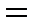
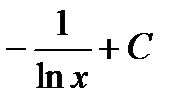
Пример 2: Найти неопределенный интеграл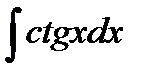

Решение: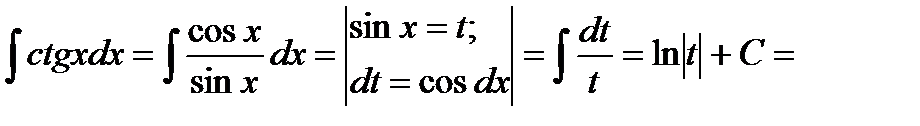

=

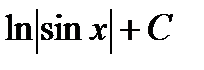
Пример 3: Найти неопределенный интеграл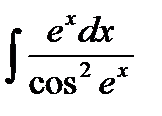

Решение: =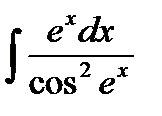

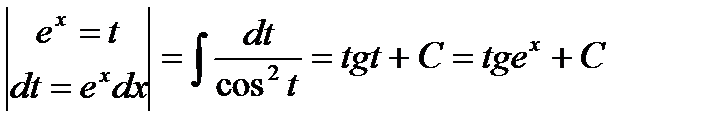
Пример 4: Найти неопределенный интеграл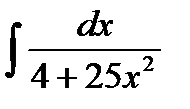

Решение: =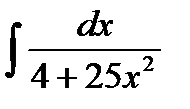

= = .

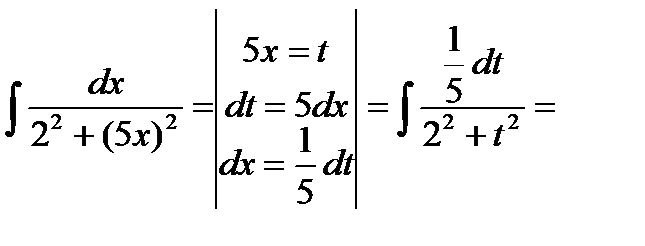
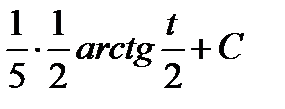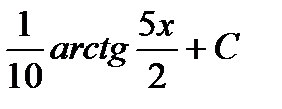Определенный интеграл и его свойства

Пусть функция 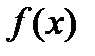определена на отрезке 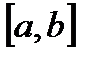. Разобьем отрезок на n частей точками 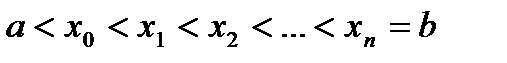, выберем на каждом элементарном отрезке 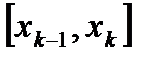произвольную точку x_k и обозначим через 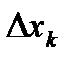длину каждого такого отрезка.

Интегральной суммой для функции 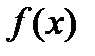на отрезке 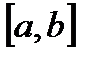называется сумма вида

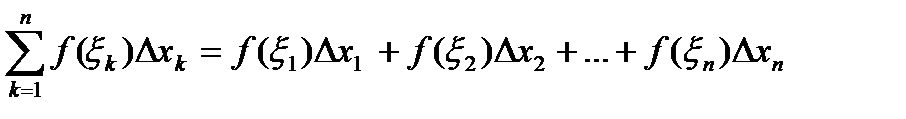
Определение:Определенным интегралом от функции 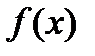на отрезке 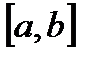называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

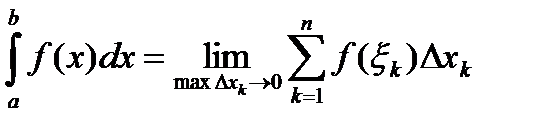
Для любой функции 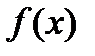, непрерывной на отрезке 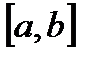, всегда существует определенный интеграл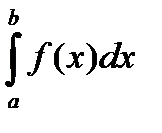

Простейшие свойства определенного интеграла

1) Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых функций:

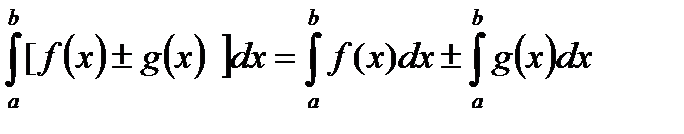
2) Постоянный множитель можно выносить за знак определенного интеграла

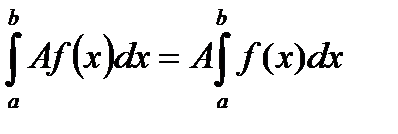
3) При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:

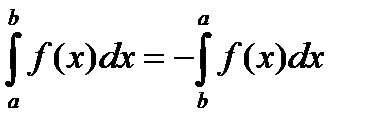
4) Определенный интеграл с одинаковыми пределами равен нулю: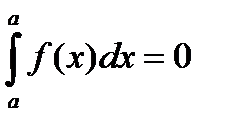

5) Отрезок интегрирования можно разделить на части:

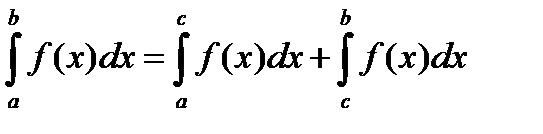
с-точка, лежащая между а и b.

6) Если 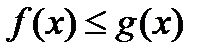на отрезке 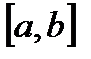, то .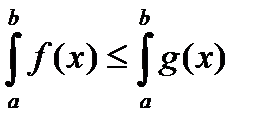

Для вычисления определенного интеграла от функции 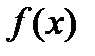, в том случае, когда можно найти соответствующуюпервообразную 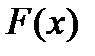, служит формула Ньютона-Лейбница:

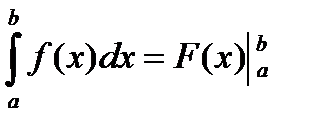=F(b)-F(a)

Рассмотрим нахождение простейших определенных интегралов.

Пример 1: Вычислить определенный интеграл .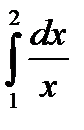

Решение: =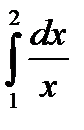

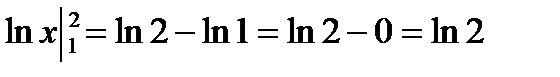
Пример 2:Вычислить определенный интеграл: .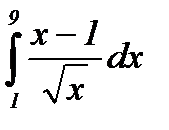

Решение: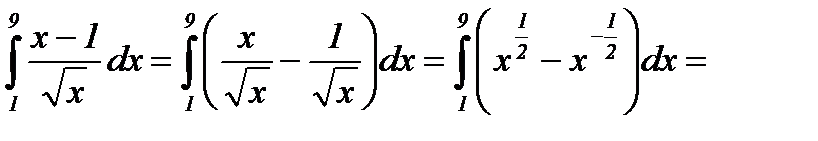

.

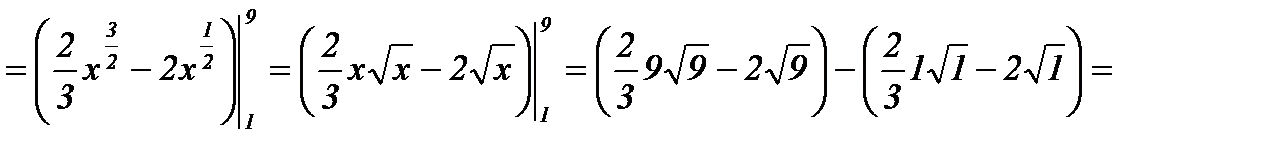
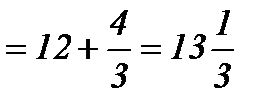Вычисление определенного интеграла

Методом замены переменной

При вычислении определенного интеграла методом замены переменной (способом подстановки) определенный интеграл 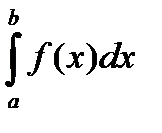преобразуется с помощью подстановк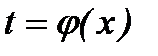и или 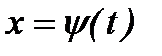в определенный интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются соответственно новыми пределами t₁ и t₂, которые находятся из исходной подстановки.

Из первой подстановки новые пределы интегрирования вычисляются непосредственно: .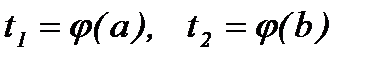

Из второй подстановки новые пределы интегрирования находятся путем решения уравнений .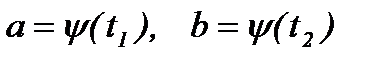

Таким образом, имеем

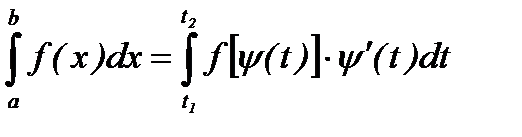
Пример 1: Вычислить определенный интеграл методом замены переменной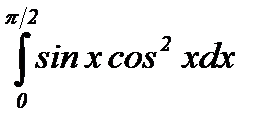

Решение: =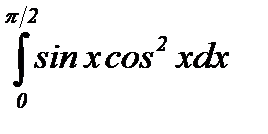

.

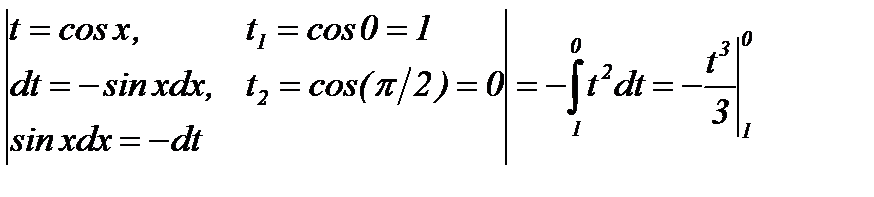
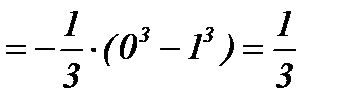Пример 2: Вычислить определенный интеграл: .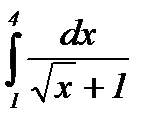

Решение: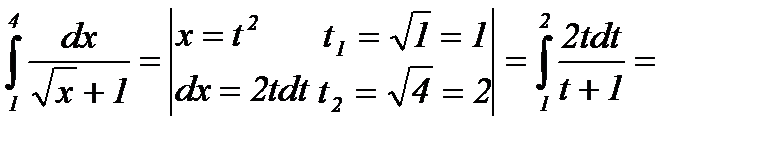

.

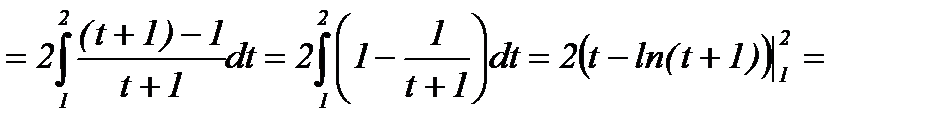
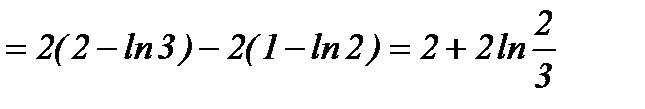Формула Ньютона-Лейбница

Чтобы получить формулу для вычисления определенного интеграла, еще раз поставим задачу о вычислении площади криволинейной трапеции.

y

М

А B

f(x)

A₁ М₁ В₁

0 a х b х

Рассмотрим криволинейную трапецию А₁АВВ₁. Возьмем некоторое значение xЄ[a, b]. Ясно, что площадь криволинейной трапеции А₁АММ₁ (заштрихованная на чертеже) зависит «х», т.е является функцией х. Обозначим эту функцию S(х). Очевидно, что S(a)=0, S(b)=S – площадь всей данной криволинейной трапеции.

Можно доказать (мы это делать не будем), что функция S(x) является первообразной для функции f(х), т.еS΄(x)=f(x)/

Пусть теперь F(x) тоже какая-нибудь первообразная для f(х), например 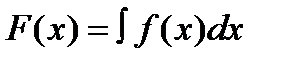. Но тогда по свойству первообразных S(x)=F(x)+C.

При х=а получим: S(a)=F(a)+C или 0=F(a)+C

Значит S(x)=F(x)-F(a). Положим здесь x=b: S(b)=F(b)-F(a) или S=F(b)-F(a), но 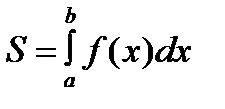следовательно .

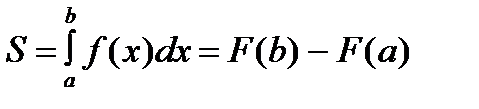Это и есть формула Ньютона-Лейбница. Она говорит, что для вычисления определенного интеграла надо сначала найти функцию F(x) первообразную для подинтегральной функции; затем в нее подставить пределы интегрирования (верхний и нижний) и затем найти разность F(b)-F(a). Поэтому иногда формулу Ньютона-Лейбница записывают подробнее:

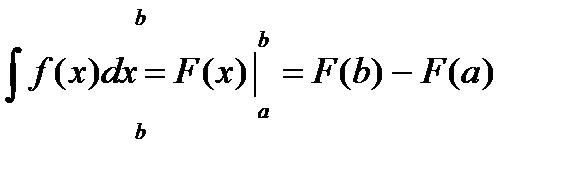
Решение типового примера

Вычислить площадь фигуры, ограниченную заданными линиями: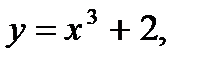

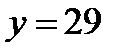
y

0 3 x

Найдем абсциссы точек пересечения заданных линий

; ; ;

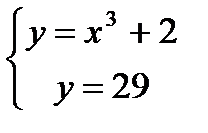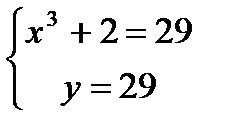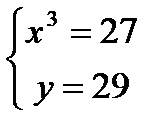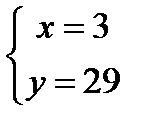
Площадь фигуры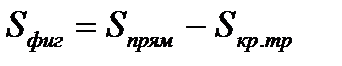

=

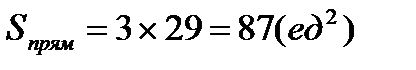
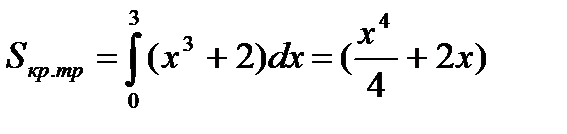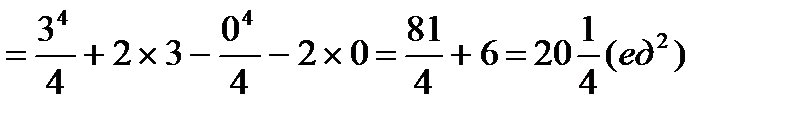
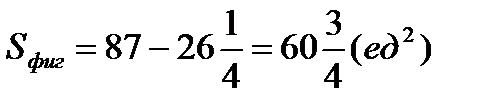
Ответ: площадь фигуры составляет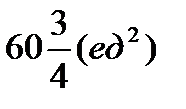

Дифференциальные уравнения

Определение:Уравнение, связывающее независимую переменнуюх, неизвестную функциюу и ее производные или дифференциалы различных порядков, называется дифференциальным уравнением.

.

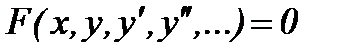Определение: Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

Определение:Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение.

(Например, y΄sinx + ytgx = 1 - первого порядка;

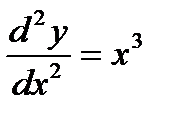- второго порядка).

Определение:Функцияy =φ(x), удовлетворяющая дифференциальному уравнению, называется решением этого уравнения. Решение дифференциального уравнения, содержащее столько независимых произвольных постоянных, каков порядок уравнения, называетсяобщим решением этого уравнения.

Для уравнения 1-го порядка: y = φ(x, C)

Определение:Функции, получаемые из общего решения при различных числовых значениях произвольнх постоянных, называются частными решениями этого уравнения.

Определение: Задача на нахождение частного решения дифференциального уравнения при заданных начальных условиях называется задачей Коши.