Теорема об эквивалентности пар сил.

Две пары, имеющие равные моменты, эквивалентны. Пусть на тело в плоскости I действует пара (F₁,F`<sub>1</sub>) с моментом M<sub>1</sub>. Эту пару можно заменить другой парой (F<sub>2</sub>, F`₂), расположенной в плоскости II, если только ее момент М₂ равен М₁. Пло­скости I и II должны быть параллельны, в частности, они могут совпадать. Из параллельности моментов M₁, и М₂ следует, что плоскости действия пар, перпендикулярные моментам, также параллельны. Введем новую пару (F₃, F`<sub>3</sub>) и приложим ее вместе с парой (F<sub>2</sub>, F`₂) к телу, расположив обе пары в плоскости II. Для этого согласно аксиоме 2 нужно подобрать пару (F₃, F`<sub>3</sub>) с мо­ментом М<sub>3</sub> так, чтобы приложенная система сил (F<sub>2</sub>, F`₂, F₃, F`₃) была уравновешена.

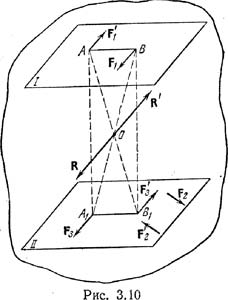
Предположим F₃=–F`<sub>1</sub> и F`₃=–F₁ и совместим точки при­ложения этих сил с проекциями А₁ и B₁ точек А и В на плоскость II (см. рис. 3.10). Следует : М₃=–M₁ или, учитывая, что М₁=М₂, М₂+М₃ = 0,получим (F₂, F`<sub>2</sub>, F<sub>3</sub>, F`₃)~0. Т.о., пары (F₂, F`<sub>2</sub>) и (F<sub>3</sub>, F`₃) взаимно уравновешены и присоединение их к телу не нару­шает его состояния (аксиома 2), так что (F₁, F`<sub>1</sub>)~(F<sub>1</sub>, F`₁, F₂, F`<sub>2</sub>, F<sub>3</sub>, F`₃). С другой стороны, силы F₁ и F₃, а также F`<sub>1</sub> и F`₃ можно сло­жить по правилу сложения параллельных сил, направленных в одну сторону. Они равны по модулю, поэтому их рав­нодействующие R и R' должны быть приложены в точке пересече­ния диагоналей прямоугольника ABB₁A₁, кроме того, они равны по модулю и направлены в проти­воположные стороны. Это означает, что они составляют систему, экви­валентную нулю. Итак, (F₁, F`<sub>1</sub>, F<sub>3</sub>, F`₃)~(R, R')~0. Теперь можем записать (F₁, F`<sub>1</sub>, F<sub>2</sub>, F`₂, F₃,F`<sub>3</sub>)~(F<sub>2</sub>, F`₂). Получим (F₁, F`<sub>1</sub>)~(F<sub>2</sub>, F`₂)и т.д. . Из этой теоремы следует, что пару сил можно перемещать и поворачивать в плоскости ее действия, переносить в параллельную плоскость; в паре можно менять одновременно силы и плечо, сохраняя лишь направление вращения пары и модуль ее момента (F₁h₁=F₂h₂).

Свойства пар сил.

Первое свойство. Пару сил нельзя привести к сил. Пара сил (как и сила) является самостоятельным элементом статики.

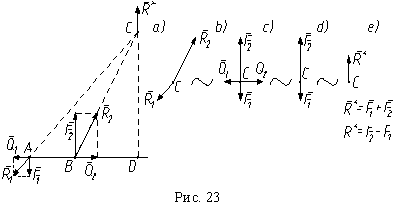Под действием пары сил свободное твердое тело может только поворачиваться. Сложим две неравные параллельные силы, направленные в разные стороны (рис. 23). Добавляем к исходной системе сил (F₁,F₂) уравновешенную систему сил (Q₁,Q₂) ~ 0. По аксиоме параллелограмма, силы, приложенные в точках A и B, эквивалентны двум непараллельным силам R₁ и R₂ (рис. 23, a). Согласно следствию второй аксиомы, переносим эти силы в точку пересечения их линий действия C (рис. 23, b). Используя вторую и третью аксиомы, раскладываем силы R₁ и R₂ на составляющие , а затем вычитаем уравновешенную систему сил (Q₁,Q₂). В результате - исходная система сил эквивалентна тем же силам, но приложенным в одной точке C, то есть (F₁,F₂) = (F₁,F₂)_C . По аксиоме параллелограмма эта система, а следовательно, и исходная система сил, эквивалентна одной силе или равнодействующей:

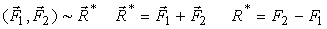(1)

Равнодействующая и ее линия действия CD параллельны исходным силам, а точка D лежит вне отрезка AB. При сложении двух параллельных сил, направленных в одну сторону, величина равнодействующей будет равна R* = F₁ + F₂, а точка D будет лежать внутри отрезка AB.

Второе свойство. Действие пары сил на твердое тело определяется моментом пары, который является свободным вектором, перпендикулярным плоскости пары, численно равным произведению силы на плечо пары.

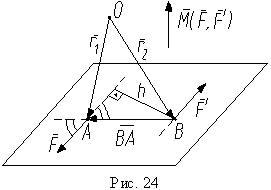
(продолжение19)Выбираем в пространстве произвольный центр O (рис. 24) и вычисляем относительно этого центра сумму моментов сил, образующих пару. Эта сумму - моментом пары. Положение точек приложения сил пары относительно центра O определяется радиус-векторами r₁, r₂ и, учитывая, что F' = -F, получим :

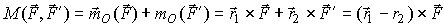Строим вектор BA, который определяет положение точки A относительно B, и на рис. 24 видим, что r₁ = r + BA или r₁ - r = BA. Учитывая это, из выражения (2) получаем:

(3)

Таким образом, действие пары сил на тело определяется ее моментом, который является мерой действия пары сил на твердое тело. Момент пары не зависит от выбора центра, то есть является свободным вектором. Величину момента пары найдем, определяя модуль векторного произведения в (3), учитывая (рис. 24), что BA sin(BA ^ F) = h:

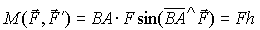
Приняв за центр O последовательно точки приложения сил A и B, по формуле (2) имеем :

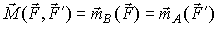
Следствия из второго свойства пары. 1. Действие пары на твердое тело не изменяется, если пару сил поворачивают в плоскости пары. 2. Действие пары сил на твердое тело не изменяется, если пару сил переносят в другое место плоскости пары. 3. Действие пары сил на твердое тело не изменяется, если ее перенести в плоскость, параллельную плоскости пары. В плоской системе сил, когда все силы и пары сил лежат в одной плоскости, моменты пар направлены перпендикулярно этой плоскости и поэтому параллельны друг другу, в этом случае, момент пары рассматривают как алгебраическую величину, равную

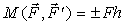(6)

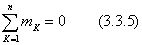20. Сложение пар сил в пространстве и плоскости.Подобно силам, пары можно складывать. Пара, заменяющая собой действие данных пар, называется результирующей. Теорема: Система пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же плоскости и имеющей момент,равный алгебраической сумме моментов слагаемых пар. Пусть на тело действуют три пары сил с моментами 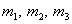. Используя теорему об эквивалентности пар, заменяем эти пары эквивалентными другими парами ,имеющими общее плечо d и такие же моменты 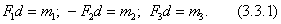Сложив отдельно силы получим: 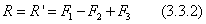Вся система заменится одной парой с моментом 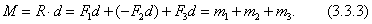Обобщая эту формулу , получим: Для равновесия плоской системы пар необходимо и достаточно, чтобы алгебраическая сумма моментов этих пар была равна нулю:

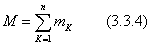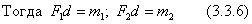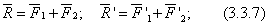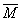При сложении пар в пространстве достаточно будет рассмотреть две пары. Теорема: Любая система пар, действующая на твердое тело, эквивалентна одной паре с моментом, равным геометрической сумме моментов слагаемых пар. Итак, пусть даны две пары с моментами m1 и m2, лежащие в плоскостях I и II . Складываем силы в точках А и В: и убеждаемся, что пары заменяются одной парой . Найдем момент этой пары:

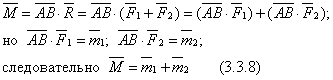Если на тело действует л пар с моментами , то:

Геометрически вектор 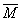- это замыкающий вектор силового многоугольника. Если векторы лежат в разных плоскостях, то можно ввести систему координат Oxyz и находить 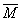аналитически:

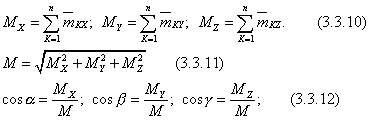
Условия равновесия пар.

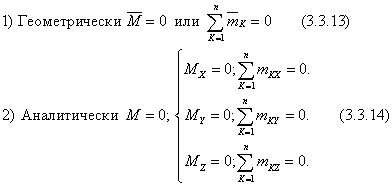Условия равновесия пространственной системы пар, запишутся:

Если в результате сложения пар 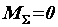, то действующие на тело пары образуют уравновешенную систему. Следовательно, необходимое и достаточное условие равновесия системы пар выражается одним уравнением
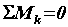,т. е. для равновесия системы пар сил, действующих на тело в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю. Значит, систему пар или одну пару можно уравновесить только парой.

22. Приведение силы к заданному центру.

Теорема о параллельном переносе силы: силу F, не изменяя ее действие на абсолютно твердое тело, можно переносить из данной точки (А) в любую другую точку (О) тела, прибавляя при этом пару с моментом (m), равным моменту переносимой силы относительно точки (О), куда сила переносится [m = m_o (F)]; F F, m. Приведение системы сил F₁, F₂, ..., F_n к произвольном центру (точке) О, т. е. замене данной системы сил другой эквивалентной более простой, происходит с помощью Теоремы Пуансо: любая система сил F₁, F₂, ..., F_n действующих на абсолютно твердое тело, при приведении к произвольному центру О заменяется одной силой R, равной главному вектору системы сил, приложенной в центре О и парой сил с моментом M_o, равным главному моменту системы сил относительно центра (точки) О. Главный вектор:

R = F1 + F2 + ... + Fn = ∑Fk, (k = 1, 2, ..., n)

а главный момент системы сил относительно центра (точки) О:

Mo = m1 + m2 + ... + mn = mo(F1) + mo(F2) + ... + mo(Fn) = mo(Fk). (k = 1, 2, ..., n)

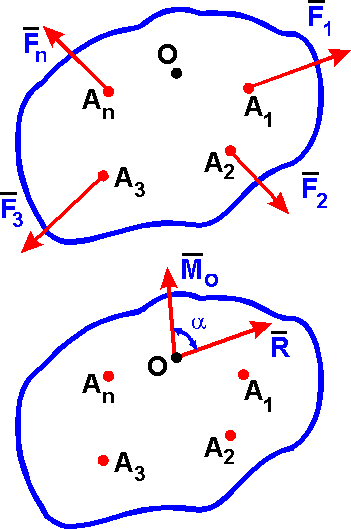Величина главного вектора R не зависит от выбора центра О, а значение главного момента M_o при изменении положения центра О может в общем случае изменяться. Для плоской системы сил F₁, F₂, ..., F_n главный вектор R лежит в плоскости действия сил, а главный момент перпендикулярен этой плоскости ( = 90). Поэтому главный момент плоской системы сил относительно центра О определяется как сумма алгебраических моментов сил относительно точки (центра) О: M_o = m_o(F_k), (k = 1, 2, ..., n) и изображается на плоскости дуговой стрелкой.