Параметры статистического распределения

Пусть изучается дискретная генеральная совокупность относительно количественного признака Х. Как правило, при исследовании этого признака интересуются следующими параметрами распределения: генеральной средней, генеральной дисперсией, генеральным средним квадратическим отклонением. В ряде случаев исследуют и другие параметры: моменты, мода, медиана.

Определение 11. Генеральной средней 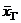называется среднее арифметическое признака генеральной совокупности.

Замечание. .

Определение 6. Генеральной дисперсией называется среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения .

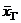Определение 7. Генеральным средним квадратическим отклонением называется величина .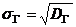

Замечание. Если исследуемый признак является непрерывным, то прежде чем оценивать его параметры, нужно составить по данным выборки интервальный ряд, а затем взять в качестве наблюдаемых значений признака середины интервалов, а в качестве частот – суммы частот значений, попавших в данный интервал.

Определение 8. Точечной называют оценку, которая определяется одним числом.

Определение 9. Интервальной называют оценку, которая определяется двумя числами – концами некоторого интервала.

Точечные оценки генеральной совокупности

Средние величины

Определение 10. Выборочной средней 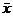называется среднее арифметическое значение признака выборочной совокупности: .

Замечание 1. Для несгруппированного вариационного ряда все частоты , а

– «невзвешенная» выборочная средняя.

Замечание 2. Выборочная средняя, найденная по данным одной выборки, есть определённое число. Если же из генеральной совокупности извлекать другие выборки того же объёма, то выборочная средняя будет изменяться от выборки к выборке. Таким образом, выборочную среднюю можно рассматривать как случайную величину, а следовательно, можно говорить о распределении (теоретическом и эмпирическом) выборочной средней и о числовых характеристиках этого распределения.

Свойства выборочной средней

Свойство 1. Выборочная средняя является несмещённой оценкой генеральной средней, т.е. .

Доказательство. Будем рассматривать 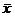как случайную величину и наблюдаемые значения , ( ) как независимые одинаково распределённые случайные величины 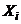, ( ). Так как эти величины одинаково распределены, то они имеют одинаковые числовые характеристики, в частности, одинаковое математическое ожидание а. Так как математическое ожидание среднего арифметического одинаково распределённых случайных величин равно математическому ожиданию каждой из величин (действительно, для 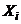, ( ) )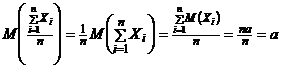, то . Так как каждая из величин 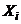, ( ) имеет то же распределение, что и генеральная совокупность (которую тоже рассматриваем как случайную величину), то и числовые характеристики этих величин и генеральной совокупности одинаковы. В частности, математическое ожидание а каждой из величин равно математическому ожиданию признака Х генеральной совокупности, т.е. 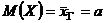. Тогда .

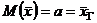Свойство 2.Выборочная средняя является состоятельной оценкой генеральной средней.

Доказательство. Допустим, что случайные величины 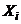, ( ) имеют ограниченные дисперсии. Тогда, применяя к этим величинам теорему Чебышева, получаем, что при увеличении п среднее арифметическое рассматриваемых величин, т.е. 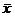как случайная величина стремится по вероятности к математическому ожиданию а каждой из величин, т.е. к генеральной средней. Следовательно, дисперсия случайной величины 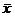при этом стремится к нулю, а это и означает, что выборочная средняя есть состоятельная оценка генеральной средней.

Следствие. Выборочные средние обладают свойством устойчивости, т.е. если по нескольким выборкам достаточно большого объёма из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближённо равны между собой.

Замечание. Если дисперсии двух совокупностей одинаковы, то близость выборочных средних к генеральным не зависит от отношения объёма выборки к объёму генеральной совокупности. Она зависит от объёма выборки: чем выборка больше, тем меньше выборочная средняя отличается от генеральной.

Будем рассматривать все значения количественного признака Х совокупности (безразлично, выборочной или генеральной). Выборочную среднюю и генеральную среднюю при таком рассмотрении будем называть средней арифметической.

Свойство 3. Средняя арифметическая постоянной равна самой постоянной.

Свойство 4. Если все варианты увеличить (или уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз, т.е. 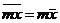или .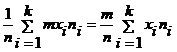

Свойство 5. Если все варианты увеличить (уменьшить) на одно и то же число, то средняя арифметическая увеличится (уменьшится) на то же число, т.е. или .

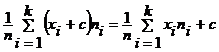Свойство 6. Средняя арифметическая суммы нескольких признаков равна такой же сумме средних арифметических этих признаков: .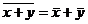

Допустим, что все значения количественного признака Х совокупности (безразлично, выборочной или генеральной) разбиты на несколько групп.

Определение 11. Групповой средней называется среднее арифметическое значений признака, принадлежащих группе.

Определение 12. Общей средней называется среднее арифметическое значений признака, принадлежащих всей совокупности.

Свойство 7. Общая средняя равна средней арифметической групповых средних, взвешенной по объёмам групп: 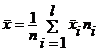, где 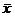– общая средняя, 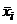– групповая средняя 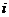-ой группы, объём которой равен 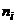, 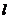– число групп.

Замечание. Для упрощения расчёта общей средней совокупности большого объёма целесообразно разбить её на несколько групп, найти групповые средние, а затем по ним – общую среднюю.

Определение 13. Отклонением называют разность 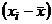между значением признака и общей средней.

Свойство 8.Сумма произведений отклонений на соответствующие частоты равна нулю, т.е .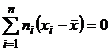

Доказательство. Общая средняя имеет вид 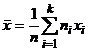. Отсюда 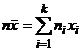. Так как 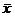– постоянная величина, то можно записать 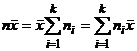. Тогда .

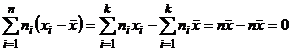Замечание. Другими словами, средняя арифметическая отклонений вариант от средней арифметической равна нулю: .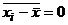

Замечание.Средние величины называют аналитическими средними. Кроме аналитических средних используются также структурные или порядковые средние.

Определение 14. Медианой 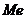вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдаемых значений.

Замечание.Ряд наблюдаемых значений называется ранжированным, если все значения расположены в нём строго по возрастанию или строго по убыванию величин. Для дискретного вариационного ряда с нечётным числом членов ( 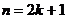, 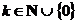) медиана равна серединному значению: 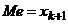, а для ряда с чётным числом членов ( 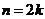, ) – полусумме двух серединных значений: 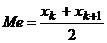. Для интервального ряда медиана может быть приближенно найдена с помощью кумуляты как значение признака, для которого 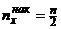или . Достоинство медианы заключается в том, что на неё не влияет изменение крайних членов ряда. Медиана предпочтительнее средней для тех вариационных рядов, у которых крайние значения по сравнению с остальными оказались слишком большими или слишком малыми.

Определение 15. Модой вариационного ряда называется то его значение, которому соответствует наибольшая частота.

Замечание.Для дискретного вариационного ряда мода находится по определению. Для интервального вариационного ряда мода может быть приближённо найдена с помощью гистограммы. Для этого нужно:

1) выбрать интервал, имеющий наибольшую частоту;

2) вершины прямоугольника, построенного на этом интервале, соединить с соответствующими вершинами соседних прямоугольников;

3) найти точку пересечения, которая и будет приближенной модой. Мода, так же, как и медиана, обладает определённой устойчивостью к вариации признака, т.е. не изменяется при изменении крайних членов ряда.

Пример 2.1. Распределение рабочих механического цеха по тарифному разряду имеет вид:

Тарифный разряд							сумма
Количество рабочих

По оплате труда рабочие разделены на 2 группы: рабочие низких разрядов (1-3) и рабочие высоких разрядов (4-6). Найти: 1) выборочную среднюю, 2) групповые средние; 3) общую среднюю, проверить свойство групповых средних; 4) моду, 5) медиану.

Решение.1) Выборочная средняя:

2) Групповая средняя для рабочих низких разрядов:

Групповая средняя для рабочих высоких разрядов:

3) Общая средняя:

4) Медиана:

5) Мода:

Пример 2.2. Из генеральной совокупности значений нормально распределенного признака Х извлечена выборка объемом :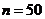

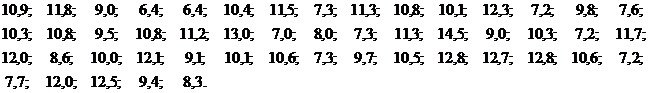
Найти: 1) выборочную среднюю, 2) медиану, 3) моду.

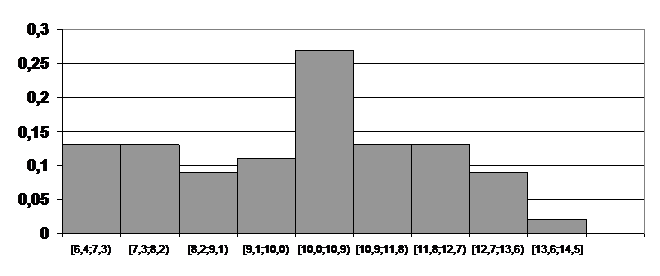
Решение. Для построения интервального вариационного ряда воспользуемся решением примера 1.2:

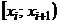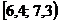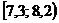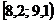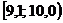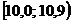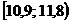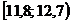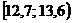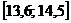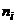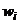	0,12	0,12	0,08	0,10	0,24	0,12	0,12	0,08	0,02
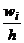	0,13	0,13	0,09	0,11	0,27	0,13	0,13	0,09	0,02

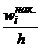1) Вычислим выборочную среднюю:

2) Для нахождения медианы воспользуемся значениями накопленных частот примера 1.2. Тогда

3) Для нахождения моды воспользуемся гистограммой примера 1.2.

Показатели вариации

Определение 16. Вариационным размахом называется разность между наибольшим и наименьшим значениями вариационного ряда: .

Определение 17. Средним линейным отклонением вариационного ряда называется среднее арифметическое абсолютных величин наблюдаемых значений от их средней арифметической: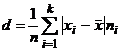

Определение 18. Выборочной дисперсией 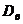называется среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения : .

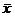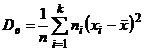Свойства дисперсии

Свойство 1. Дисперсия постоянной равна самой постоянной.

Свойство 2. Если все варианты увеличить (или уменьшить) в одно и то же число раз, то дисперсия увеличится (уменьшится) во столько же раз, т.е. 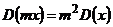или .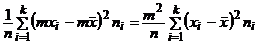

Свойство 3. Если все варианты увеличить (уменьшить) на одно и то же число, то дисперсия не изменится, т.е. или .

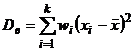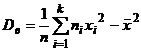Свойство 4. Для вычисления дисперсии можно также применять следующие формулы: 1) , 2) , 3) .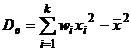

Доказательство: 1) Формула получается после внесения 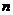под знак суммы и переобозначения частного .

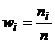2)

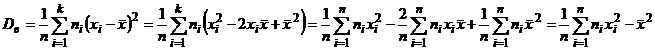
3) Формула получается после переобозначения .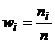

Замечание. Свойство можно записать в виде: , где .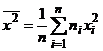

Допустим, что все значения количественного признака Х совокупности (безразлично, выборочной или генеральной) разбиты на несколько групп.

Определение 19. Групповой дисперсией называется дисперсия значений признака, принадлежащих группе, относительно групповой средней: , где 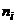– частота значения , 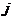– номер группы, 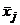– групповая средняя группы 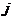, – объём группы .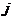

Определение 20. Внутригрупповой дисперсией называют среднюю арифметическую групповых дисперсий, взвешенную по объёмам групп: 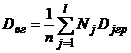, где 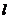– число групп, .

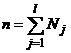Определение 21. Межгрупповой дисперсией называют дисперсию групповых средних относительно групповой средней: .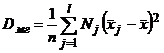

Определение 22. Общей дисперсией называется дисперсия значений признака всей совокупности: .

Свойство 5. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий: .

Доказательство. Для упрощения доказательство предположим, что вся совокупность значений количественного признака Х разбита на 2 группы со следующими характеристиками:

Группа	Первая	Вторая
Значение признака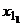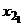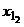
Частота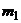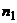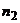
Объём группы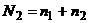
Групповая средняя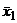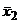
Групповая дисперсия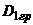
Объём совокупности

Найдём общую дисперсию:

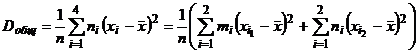. (3.1)

Преобразуем первое слагаемое числителя, вычтя и прибавив :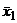

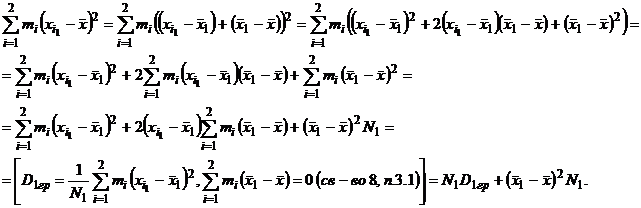
Таким образом, 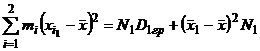(3.2)

Аналогично можно представить второй слагаемое числителя (3.1), вычтя и прибавив 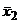: 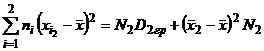(3.3.)

Подставим (3.2) и (3.3) в (3.1), получим:

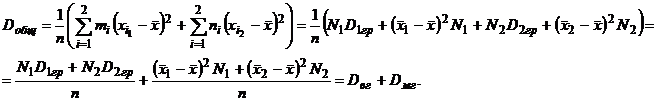
Замечание.Теорема имеет важное практическое значение. Например, если в результате наблюдений получены несколько групп значений признака, то для вычисления общей дисперсии можно группы в единую совокупность не объединять. С другой стороны, если совокупность имеет большой объём, то целесообразно разбить её на несколько групп. И в том и в другом случаях непосредственное вычисление общей дисперсии заменяется вычислением отдельных групп, что облегчает расчёты.

Свойство 6. Если случайная выборка состоит из 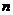независимых наблюдений над случайной величиной Х с математическим ожиданием 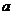и дисперсией 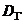, то выборочная дисперсия является смещённой оценкой генеральной дисперсии.

Доказательство. Пусть 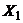, , 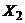…, 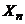– 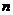независимых наблюдений над случайной величиной Х. По условию 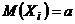, ( 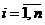) и .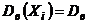

Преобразуем формулу выборочной дисперсии:

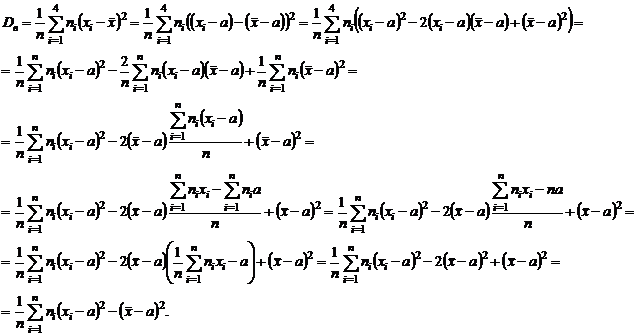
Рассмотрим математическое ожидание выборочной дисперсии:

Таким образом, выборочная дисперсия является смещённой оценкой генеральной дисперсии.

Замечание. Выборочная дисперсия является состоятельной оценкой генеральной дисперсии.

Определение 23. Выборочным СКОназывается величина .

Замечание. Для получения несмещённой оценки генеральной дисперсии вводят следующую величину.

Определение 24. Исправленной выборочной дисперсией называется величина

.

Замечание. Исправленная выборочная дисперсия является несмещённой состоятельной оценкой дисперсии генеральной совокупности. Действительно,

.

Определение 21. Исправленным выборочным СКОназывается величина

.

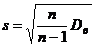Замечание 1. Исправленное выборочное СКО не является несмещённой оценкой генерального СКО.

Замечание 2.Сравнивая и 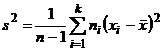, видим, что они отличаются лишь знаменателями, т.е. при достаточно больших значениях 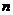выборочная и исправленная дисперсии отличаются мало. На практике пользуются исправленной выборочной дисперсией, если 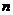<30.

Пример 2.3. Распределение рабочих механического цеха по тарифному разряду имеет вид: (см. примеры 1.1. и 2.1).

Тарифный разряд							сумма
Количество рабочих

По оплате труда рабочие разделены на 2 группы: рабочие низких разрядов (1-3) и рабочие высоких разрядов (4-6). Найти: 1) выборочную дисперсию, 2) групповые дисперсии; 3) межгрупповую дисперсию; 4) исправленную выборочную дисперсию.

Решение.Воспользуемся тем, что выборочная средняя равна групповые выборочные средние соответственно равны:

1) Выборочная дисперсия:

2) Групповая выборочная дисперсия для рабочих низких разрядов:

Групповая выборочная дисперсия для рабочих высоких разрядов:

3) Межгрупповая дисперсия

4) Исправленная выборочная дисперсия: