Проблема разрешимости тождественной истинности

Ввиду особой роли ТИФ, возникает вопрос о существовании общего метода (разрешающего метода), позволяющего относительно любой конкретной формулы логики высказываний ответить, является ли она тождественно истинной или нет.

Укажем несколько методов разрешения этого вопроса.

1. Составление таблицы истинности, соответствующей данной формуле. Если последний столбец таблицы (столбец значений данной формулы) состоит из одни И, данная формула – ТИФ, если же в столбце содержится хотя бы одна Л, она не является ТИФ. Разумеется, составление таблицы истинности ‑ не всегда удобный метод (при числе n переменных таблица содержит 2ⁿ строк). Но она всегда состоит из конечного числа шагов и всегда дает ответ на поставленный вопрос.

2. Преобразование формулы (приведение ее к КНФ). Все операции, знаки, которые содержатся в формуле, выражаются через конъюнкцию, дизъюнкцию и отрицание. Знаки отрицания сводятся к отдельным переменным (использование законов де Моргана). Для этого используются законы двойного отрицания, коммутативности, ассоциативности конъюнкции и дизъюнкции, дистрибутивности дизъюнкции относительно конъюнкции.

В результате этих преобразований формула приводится к КНФ. Если в каждой дизъюнкции содержится какая-либо переменная вместе с ее отрицанием, то данная формула – ТИФ. Если существует хотя бы одна дизъюнкция, не содержащая ни одной переменной вместе с ее отрицанием, данная формула не является ТИФ.

Пример. Применим этот метод к формуле (pÞq)(qÞr) Þ (pÞr)

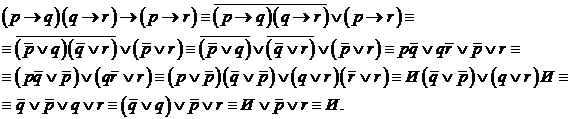
3. Метод косвенного доказательства (способ от противного). Допустим, что данная формула не является ТИФ. Тогда существует хотя бы один набор значений переменных, входящих в эту формулу, при котором она принимает значение Л. Если такой набор переменных удается найти, то данная формула не является ТИФ. Если же допущение о существовании такого набора значений переменных ведет к противоречию, то данная формула – ТИФ.

Пример. Применим этот метод к формуле (pÞq)(qÞr) Þ (pÞr).

Допустим, что эта формула не является ТИФ. Тогда существует хотя бы один набор значений переменных (p, q, r), при котором она ложна, то есть основание истинно

(pÞq)(qÞr)ºИ; (1)

а следствие ложно (pÞr)ºЛ. (2)

Из (2) следует р=И, (3)

а r=Л (4)

Из (1) следует, что (pÞq)ºИ; (5)

(qÞr)ºИ; (6)

Из (6) и (4) следует q=Л, (7)

а из (7) и (5) р=Л. (8)

Получили противоречие (3) и (8). Следовательно, наше допущение неверно и формула (1) ТИФ.

На основе этих примеров можно сделать ряд выводов о тождественной истинности формул.

Теорема 1. Чтобы элементарная логическая сумма была тождественно-истинной, необходимо и достаточно, чтобы в ней содержалась хотя бы одна пара слагаемых, из которых одно есть некоторая переменна, а другое – ее отрицание.

В самом деле, если такая пара слагаемых найдется, то сумма имеет вид 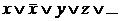Поскольку 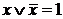, поэтому и истинна вся рассматриваемая сумма, каковы бы ни были остальные слагаемые y, z,…

Это условие достаточное. Теперь об условии необходимом. Допустим, что такой пары слагаемых, из которых одно является отрицанием другого, в сумме нет. В таком случае можно каждой переменной, не стоящей под знаком отрицания, дать значение Л, а каждой переменной, стоящей под знаком отрицание дать значение И. Это можно сделать, поскольку ни одна переменная не входит в сумму одновременно с отрицанием и без отрицания. После указанной подстановки каждое слагаемое примет значение Л, и, следовательно, формула не является ТИФ, что и требовалось доказать.

Аналогично доказывается

Теорема 2. Чтобы элементарное произведение было тождественно ложным, необходимо и достаточно, чтобы в нем содержалась хотя бы одна пара множителей, из которых один является отрицанием другого.

Элементы теории графов

Теория графов представляет в распоряжение инженера исклю­чительно удобный аппарат для моделирования структурных свойств систем и отношений между объектами самой разнообразной при­роды. На основе аналогии между физическими величинами развива­ется методика построения математических моделей систем в раз­личной форме.

Основные понятия и определения

Граф — это система некоторых объектов вместе с парами этих объектов, изображаются отношения связи между ними.

Графом G называется система (V,U,j), где V={n} — множество вершин; U={u} — множество ребер; j — функция инциденции, ста­вящая в соответствие каждому ребру uÎU упорядоченную (или не­упорядоченную) пару вершин (n₁,n₂), называемых концами ребра u.

Множество vUu образует множество элементов графа. По количеству элементов графы делятся на конечные и бесконечные.

Если j(u)= (n₁,n₂) — упорядоченная пара, (т.е. (n₁ ¹n₂)Ù(n₁,n₂)¹ (n₂,n₁)), то ребро n называется ориентированным ребром или дугой, исходящей из вершины n₁ (начало), и входящей в вершину n₂ (конец дуги).

Если j(u)=(n₁,n₂) — неориентированная пара, то соответствую­щее ей ребро — неориентированное.

Граф с неориентированными ребрами называют неориентиро­ванным, а с ориентированными ребрами — неориентированным графом (орграфом).

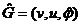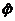Всякому графу G(v,u,j) можно сопоставить соотнесенный не­ориентированный граф , где — сопоставляет ребрам те же пары вершин, что и j, но неупорядоченные.

Граф, имеющий как ориентированные, так и неориентирован­ные ребра, называется смешанным.

Граф G=(v,u,j), ребрами которого являются всевозможными пары j(u)=(n_i,n_j) для двух возможных вершин n_i,n_jÎV, называется полным неориентированным графом. Такие графы для трех, четырех и пяти вершин приведены:

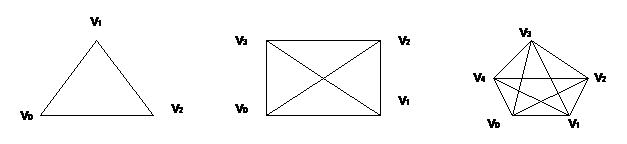
Граф G=(v,u,j), в котором пара вершин соединяется несколькими (кратными) ребрамиб называется мультиграфом, а содержащий изолированные вершины — нуль-графом.

Дополнением графа G=(v,u,j) является граф G_к=(v,u,j), ребра которого совместно с графом G образуют полный граф.

Ребро, граничными вершинами которого является одна и та же вершина, называется петлей. В общем случае граф может содержать изолированные вершины, которые являются концами ребер и не связаны между собой, ни с другими вершинами.

Число ребер, связанных с вершиной n_i (петля учитывается два­жды), называют степенью вершины.

Цепи и циклы графов

Цепь — конечная или бесконечная последовательность ребер S=(…n₁,n₂,…), в которой у каждого ребра n_к одна из вершин явля­ется вершиной ребра n_к-1, при этом ребро и одна из вершин могут встречаться несколько раз. Каждая цепь имеет начальную и конеч­ную вершину, остальные вершины называются внутренними (про­межуточными).

Цепь называется простой, если любое реьро не повторяется в цепи дважды. Составной (сложной) в противном случае; элементар­ной, если в ней ни одна из вершин не повторяется дважды.

Цикл — конечная цепь, начинающаяся и заканчивающаяся на той же вершине.

Цикл называется простым, если все его ребра различны, в ином случае — составным (сложным), и элементарным — если при об­ходе его ни одна из вершин не встречается дважды.

Цикл, не содержащий вершины, кроме той, на которой он начи­нается и заканчивается, называется петлей.

Цикл, у которого начальная и конечная вершины различны, на­зывается путем.

Он также может быть простым (никакая дуга не встречается дважды), составным или элементарным (никакая вершина не встре­чается дважды).

Длина пути — число ребер (дуг) в нем.

Цикл, начинающаяся и заканчивающаяся в начальной вершине, называется контуром.

Граф называется конечным, если число вершин его конечно, и бесконечным — в ином случае.

Граф Н(v,u,j) называется частичным для графа G(v,u,j), если все ребра и вершины графа Н, являются соответственно ребрами и вершинами графа G, т.е. если НÌG, то для всех n ÎV.

Нуль-граф считается частичным графом любого графа. Все частичные графы Н_i для G(v,u,j) можно получить, выбирая в качестве ребер всевозможные подмножества ребер графа G.

Подграфом G_А(А) графа G(v) называется граф, вершинами кото­рого являются вершины АÌv, а ребрами — все ребра из G, оба конца которых лежат в А.

Иначе, G_А(А) подграф графа G(v), если АÌv и G_А(v)=G(v)ÇА.

Если А=v, то G_А(А)=G(v); если А={а}, т.е. А состоит из одной вершины, то G_А(а) состоит из петель в а; если АÌv — подмножество изолированных вершин графа G(v), то подграфом графа G(v) будет нуль-граф.

Частичным подграфом Н_А(А), АÌХ графа G(v) называется подграф, ребрами которого являются некоторые ребра из G(v), оба конца которых лежат в А.

Иначе, Н_А(А) — частичным подграф графа G(v), если АÌХ и Н_А(v)=G(v)ÇА для всех vÎV.

Дополнительным частичным подграфом Н_А(А) графа G(v) является единственный граф, состоящий из ребер графа G(v), не принадлежащих некоторому частичному подграфу Н_А(А) графа G(v).

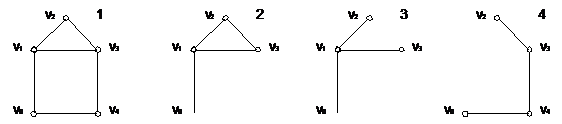1 - Граф G(v).

2 - Подграф G_А(А) графа G(v).

3 - Частичный подграф Н_А(А) графа G(v).

4 - Дополнительный частичный подграф Н_А(А) графа G(v).

Звездным графом, определяемым вершиной v, называется граф, состоящий из ребер G(v), имеющих v концевой вершиной. При этом петли в v могут включаться, либо не включаться в звездный граф.

Две вершины n_i и n_j неорганизованного графа G(v) называются связными, если существуюет цепь S с концами n_i и n_j. При прохож­дении пути через некоторую вершину n_к более одного раза цикл в вершине n_к можно удалять из цепи S.

Неориентированный граф называется связным, если любая пара его вершин связана. Отношение связности для вершин графа явля­ется отношением эквивалентности. Оно разбивает множество вер­шин графа на классы.

Подграфы, ''натянутые'' на эти классы вершин, называются компонентами связности графа. Другими словами, компонентами связности неориентированного графа G(v) называется подграф Н_А(А) с множеством вершин АÌv и множеством ребер в G(v), инцидентных только вершинам из А, причем ни одна из v_iÎA не смежна с верши­нами из множества vÇА.

Несвязный граф состоит из нескольких отдельных частичных подграфов:

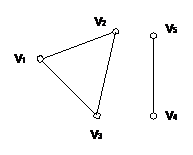
В сильно связанном ориентированном графе для любой пары вершин обязательно существует соединяющий их путь. Компонентой сильной связности ориентированного графа G(v) называется сильно связанный подграф Н_А(А) с множеством вершин АÌv и множеством дуг, имеющих начало и конец в множестве А, причем ни одна из вершин v_iÎA и ни одна из вершин v_jÎ vÇА не смежны между собой. Очевидно, что сильно связанный ориентированный граф имеет только одну компоненту сильной связности. Пример ориентированного графа, состоящего из 2-х компонент сильной связности, приведен ниже

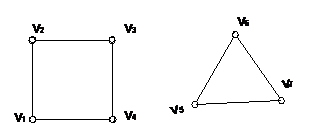
Отдельными, широко используемыми видами графов являются деревья и прадеревья.

Деревом называется конечный связный граф, состоящий по крайней мере из двух вершин и не содержащий циклов.

Такой граф не имееи кратных ребер:

Ветвями дерева называются ребра графа, входящие в дерево.

Хордами дерева называют ребра, взодящие в граф, дополнительный к данному графу.

Деревья на множестве вершин

Пусть множество v содержит р вершин, которые пронумерованы v₁,… v_р. Связав эти вершины (р-1) ребрами так, чтобы отсутствовали циклы, получим некоторое дерево, покрывающее данное множество р вершин. При р=2 такое дерево единственное и состоит из одной ветви. С увеличением р число различных деревьев t_p быстро возрастает

t_p=р^р-2

многие из них являются изоморфными, т.е. отличаются только нумерацией вершин. Так при р=0 имеем 10⁸ различных деревьев, из которых 106 неизоморфны.

На рис. показаны 16 различных деревьев, которые можно построить на множестве четырех вершин.

Символ дерева

Любому дереву Т можно поставить во взаимно-однозначное соответствие некоторый символ — упорядоченную последовательность (р-2) номеров вершин a(Т)=(a₁,a₂,… a_р-2), среди которых могут быть повторяющиеся, причем a₁,a₂,… a_р-2În.

Эта последовательность для данного дерева образуется следующим образом.

Вводится последовательность N_p=(1,2,…р), далее выбирается концевая вершина с наименьшим номером и записывается номер a,связанной с ней вершиной, а сама концевая вершина удаляется из последовательности N_p=(1,2,…р). Затем этот процесс повторяется до тех пор, пока не получим последовательность a(Т)=(a₁,a₂,… a_р-2). Каждый такой шаг соответствует удалению из дерева концевой вершины с наименьшим номером и связанного с ней концевого ребра, причем (р-2) шагов от дерева остается единственное ребро, положение которого определяется парой номеров вершин, остав­шихся в последовательности N_p. Построение дерева по его символу выполняется последовательным восстановлением концевых вершин и ребер.

На первом шаге из последовательности N_p=(1,2,…р) выбирается наименьший номер a_min, который отсутствует в a(Т)=(a₁,a₂,… a_р-2) и строится ребро (a_min,a₁). Далее удаляется номер a_min из N_p и номер a₁ из a(Т) и процесс продолжается до исчерпывания символа a(Т). оставшаяся в последовательности N_p пара вершин определяет последнее ребро дерева.

Например, исходя из символа a(Т₂)=(1,3,1,1,3) дерева Т₂

.

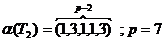последовательность N₇=(1,2,3,4,5,6,7) на первом шаге имеем ребро (2,1). Удаляя ''2'' из N₇ и ''1'' из a(Т₂), получаем последовательность

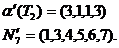
На втором шаге получаем ребро (4,3) и далее аналогично ребра (5,1),(6,1),(1,3),(3,7). Совокупность всех полученных ребер и обра­зует соответствующее дерево.

Произвольное дерево на множестве р вершин можно рассмат­ривать как одно из покрывающих деревьев графа.

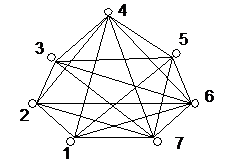
Рис. Дерево полного графа.

Экстремальное дерево.

В ряде практических задач требуется связать р пунктов наибо­лее экономичным способом с линиями связи р пунктов, автомобиль­ными дорогами таким образом, чтобы суммарная длина была наи­меньшей.

На языке теории графов эта задача формулируется в общем виде следующим образом.

Каждому ребру (n_i,n_j) полного графа с р вершинами приписыва­ется вес m_ij, выражающий численно расстояние, стоимость и другую величину, характеризующую любую пару вершин.

Требуется построить экстремальное дерево, связывающее все вершины так, чтобы был минимальным суммарный вес m_i ветвей дерева

.

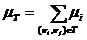Перебор вариантов при р³9 больше 10⁶. Существует алгоритм Прима, который основан на последовательном введении выбора ре­бер с наименьшим весом. Затем на каждом следующем шаге выби­рается min по весу ребро и, если оно не образует цикла с ранее вы­бранными ветвями, вводится в дерево. Построение заканчивается после отбора дерева (р-1) ребер. Если имеются ребра с одинаковым весом, то решение может быть единственным в том случае, когда не все такие ребра входят в дерево, а отдается определенный приоритет отдельным.

Построение экстремального дерева с максимальным суммар­ным весом аналогично, необходимо лишь последовательно выбирать для него ребра наибольшего веса.

Деревья графа.

Будем называть деревом связного графа любое покрывающее дерево, связывающее все его вершины и имеющее в качестве ветвей ребра этого графа.

Два дерева считаются различными, если они отличаются хотя бы одним ребром.

Существует простой способ определения количества различных деревьев графа без петель (мультиграфа) с р вершинами. Для этого необходимо записать квадратичную матрицу р-го порядка, по глав­ной диагонали которой расположена степень вершин, а ij-и ji-элементы равны взятому со знаком ''-'' числу ребер, связывающих вершины i и j.

Вычисляя любой из главных минора этой матрицы, получим исходное число деревьев.

Например, для графа имеем дерево (одно из 7в).

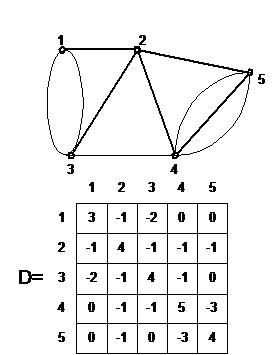
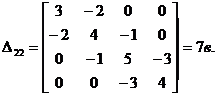
D₂₂ — один из главных миноров этой матрицы.

Это теорема Трента.

Типы конечных графов.

Число ребер, связанных с вершиной n_i (петля учитывается два­жды), называется степенью вершины и обозначается deg(n_i).

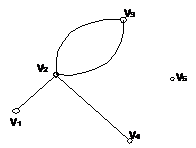
deg(n₂)=4

deg(n₅)=0

Степень изилирования вершины равна 0. Легко показать, что в любом графе сумма степеней всех вершин равна удвоенному числу ребер, а число вершин нечетной степени всегда четно.

В орграфе различают положительные d ⁺(n_i) и отрицательные d ^-(n_i) степени вершин, которые равны соответственно числу исходящих из n_i и заходящих в n_i дуг.

Очевидно, что суммы положительных…………………………….

Примеры и задачи.

1. Даны два множества Х={x₁,x₂,x₃,x₄,x₅,x₆} Y={y₁,y₂,y₃,y₄}

и определено бинарное отношение А={(x₁,y₂),(x₂,y₁),(x₂,y₂),(x₄,y₂), (x₄,y₃),(x₅,y₁),(x₅,y₃)}.

Для данного отношения А:

а) записать область определения и область значений;

б) определить сечения по каждому элементу из Х;

в) определить сечения по подмножествам Х'={x₁,x₄} и Х''={x₂,x₃,x₅} множества Х;

г) записать матрицу и нарисовать граф;

д) определить симметричное отношение А^-1.

2. Пусть Х — множество студентов; Y — множество дисциплин и соотношение хАу, где хÎХ и уÎY, означает ''студент х изучает дис­циплину у''. Дать словесное описание областей определения и значе­ний, сечений и обратного отношения, полученных в задаче №1.

3. По результатам задачи определите множества А(х₂) Ç А(х₄), А(х₂)\ А(х₄) и А(х₂)+А(х₄). Дайте им словесное описание согласно условия задачи №2.

Задача. Представьте бинарные отношения, заданные графом как множество упорядоченных пар и запишите его матрицу.

Задача. Записать композицию С=ВА отношений А={(1,2),(1,3), (2,1),(2,4),(3,3)} и В={(1,1),(1,3), (2,2),(3,1),(4,2),(4,3)}. Проверить результат с помощью операций над матрицами и графами заданных отношений.

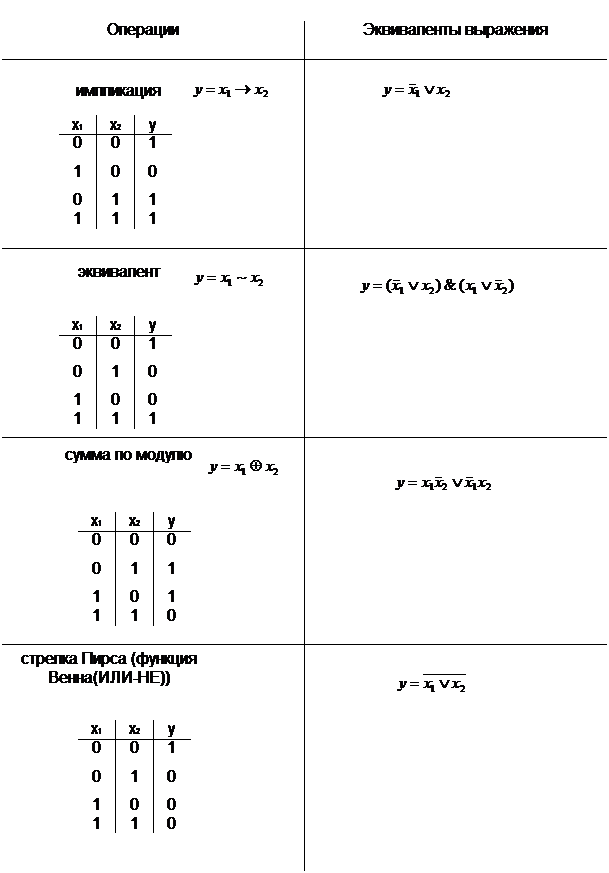
Тождества теории множеств

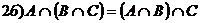
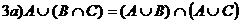
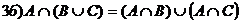
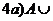Æ=A

Æ

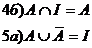
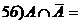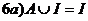
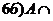Æ=Æ

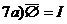
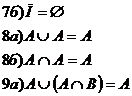
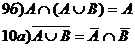
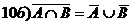
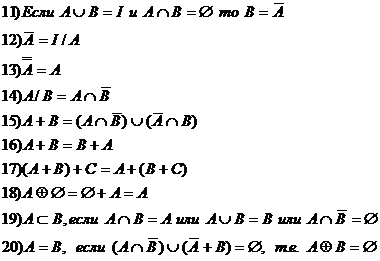
Важнейшие зависимости ФАЛ.

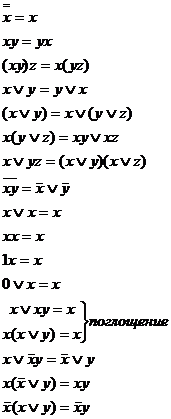
Вопросы

1. Основные понятия и терминология теории множеств:

множество, элемент, конечные и бесконечные способы задания множеств, ординарность, экстраординарность, пустое множество, собственное, несобственное, симметричное, рефлексивность, тран­зитивность.

2. Взаимно одиозное соответствие между множествами.

3. Счетные и несчетные множества.

4. Верхняя и нижняя границы множеств.

5. Операции над множествами.

6. Универсальное множество, дополнение множест

7. Разбиения множества.

8. Тождества алгебры множеств.

9. Коммутативные и дистрибутивные законы.

10. Теоремы де Моргана в алгебре множеств.

11. Дизъюнктивная сумма (коммутативный и распространитель­ный законы).

12. Принципы двойственности.

13. Метод доказательств тождеств.

14. Отношение в множествах:

рефлексивность, нерефлексивность, антирефлексивность, сим мет­ричность, асимметричность, транзитивность, связанность (доказать приведением высказываний).

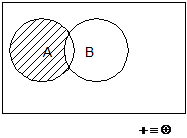
15. (M/N)Ç(N/M)=?

(АÇВÇС)È( =?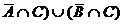

16. Решить уравнение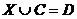

17. Принцип решения уравнений.

18. Круги Эйлера для доказательства тождеств.

19. Круги Эйлера при решении уравнений.

20. Диаграммы Венна для доказательства тождеств.

21. Диаграмма Венна для решения тождеств.

22. Сравнительный анализ методологии применения кругов Эйлера и диаграмм Венна.

23. Произведение множеств.

24. Области определения и значений.

25. Сечения, матрица отношений.

26. Граф отношения, симметричное отношение.

27. Композиция отношений.

28. Общие свойства отношений.

29. См. примеры 65.

30. Произведение множеств. Проекция множеств.

31. Соответствие в множествах.

32. Обратное соответствие. Способы задания соответствий.

33. Композиция соответствий.

34. Графическое задание объединения и пересечения соответствий.

35. Отображения, свойства их, композиция соответствий.

36. Отображение как функция.

37. Способы задания функции.

38. Функция времени, понятие оператора.

39. Понятие изоморфизма.

Комбинаторика

1. Выборка элементов. Правило суммы и произведение.

2. Перестановки.

3. Сочетание.

4. Рекуррентные соотношения.

5. Бином Ньютона.

6. Принцип включения и исключения.

Элементы алгебры логики

1. Понятие высказываний. Логические операции.

2. Логические функции.

3. Функции АЛ и основные свойства.

4. Элементарные ФАЛ и их взаимосвязи.

5. Свойства &, V отрицания.

6. Свойства по модулям, импликационным функциям Шеффера.

7. Основные классы ФАЛ.

8. Аналитическая запись ФАЛ посредством характеристических функций.

9. Алгоритм записи ФАЛ в ДНФ.

10. Алгоритм записи ФАЛ в КСНФ.

11. Полная система ФАЛ. Минимизация ФАЛ аналитическим путем.

12. Минимальная форма ФАЛ. Склеивания, поглощения.

13. Минимизация геометрическим путем.

14. Минимизация при помощи карт Карно.

Литература

1. Основы кибернетики. Математические основы кибернетики / Под ред. К.А. Пупкова М: ВШ, 1974.

2. Лапа В.Т. Математические основы кибернетики. Киев: ВШ, 1974.

3. Коршунов Ю.М. Математические основы кибернетики. М: Энергоиздат, 1987.

4. Фудзисава Т., Касами Т., Математика для использования теории дискретных структур. М: Р и С, 1984.

5. Сигорский В.П. Математический аппарат инженера. Киев: 1974.

6. Поспелов Д.А. Логические методы анализа и синтеза схем. М: Энергия, 1976.

7. Столяр А.А. Логическое введение в математику. Минск, 1971.

8. Алферова Теория алгоритмов. М: Статистика, 1973.

9. Гиндикин С.Г. Алгебра логики в задачах. М: 1972.