Глава 2. Динамика относительного движения точки

Основное уравнение динамики относительного движения точки

Рассмотрим теперь движение материальной точки, наблюдаемое из подвижной системы координат. Из кинематики известно, что такое относительное движение существенно отличается от абсолютного движения, наблюдаемого из основной (неподвижной) системы координат. Выведем далее динамические уравнения, позволяющие изучать относительное движение точки.

В п. 1.1. для абсолютного движения получено основное уравнение динамики точки

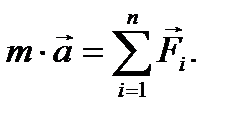
Здесь 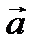- абсолютное ускорение точки относительно неподвижной системы координат. В соответствии с кинематической теоремой Кориолиса абсолютное ускорение равно геометрической сумме относительного, переносного и кориолисова ускорений

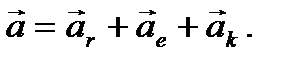(8)

Подставим выражение (8) в предыдущее равенство, получим

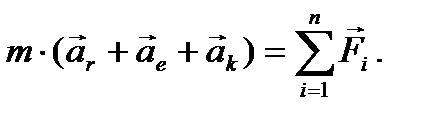
Выражая отсюда 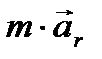через остальные члены, получим

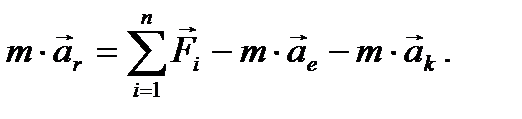(9)

Отсюда следует, что относительное ускорение создают не только обычные силы, действующие на точку, но и еще два вектора, получившие специальные названия.

Векторная величина, равная по модулю произведению массы точки на модуль переносного ускорения и направленная противоположно переносному ускорению, называется переносной силой инерции:

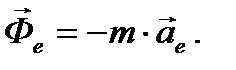(10)

Векторная величина, равная по модулю произведению массы точки на модуль кориолисова ускорения и направленная противоположно кориолисову ускорению, называется кориолисовой силой инерции:

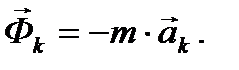(11)

Пользуясь равенствами (10) и (11), выражение (9) можно представить в виде

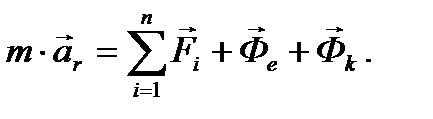(12)

Уравнение (12) называют основным уравнением динамики относительного движения точки.

Оно выражает динамическую теорему Кориолиса: относительное движение точки происходит не только под действием обычных сил, приложенных к точке, но и под действием переносной и кориолисовой сил инерции.

Из векторного равенства (12), записав его в проекциях на оси подвижной системы координат, можно получить дифференциальные уравнения относительного движения точки.

Формально введенные по формулам (10),(11) силы инерции таковы, что для объекта, помещенного в подвижную систему координат, их действие реально ощущается и неотличимо от действия обычных сил. Однако наблюдатель, находящийся в неподвижной системе координат, может объяснить их действие характером движения подвижной системы координат.

Пример 3

Горизонтальная трубка ОА длиной 1 м закреплена на вертикальной оси (см. рис. 4). В трубку помещен шарик М на расстоянии 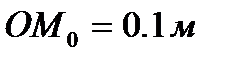от оси. После этого трубка начинает вращаться с постоянной угловой скоростью 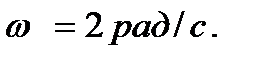Пренебрегая трением, определить, через сколько времени шарик вылетит из трубки. Движение началось из состояния покоя.

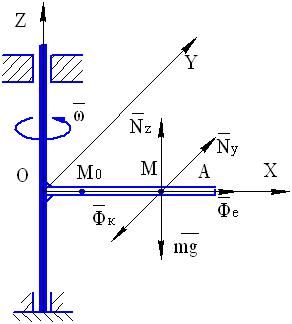
Рис. 4

Решение

Для изучения относительного движения шарика по отношению к трубке выберем подвижные оси координат, связанные с трубкой с началом в точке О на оси вращения ( см. рис. 4 ). Изобразим на рисунке шарик в промежуточном положении М и действующие на него силы - силу тяжести 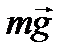и нормальную реакцию трубки, которую разложим на две составляющих 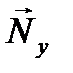и 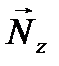. В соответствии с уравнением (12) к этим силам надо добавить переносную и кориолисову силы инерции, величины которых в данном случае найдутся по формулам

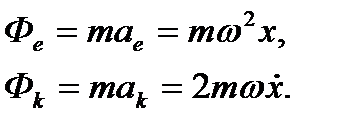
Направления этих сил инерции, противоположные направлениям соответствующих ускорений показаны на рис. 4.

Составим теперь дифференциальное уравнение относительного движения шарика, записав векторное равенство (12) в проекциях на ось х , вдоль которой происходит движение

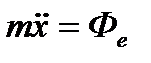
или

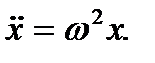
Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Составим для него характеристическое уравнение

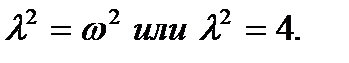
Корни этого уравнения равны 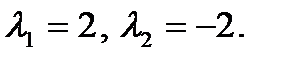Теперь решение дифференциального уравнения запишется в виде

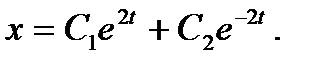(13)

Для нахождения постоянных интегрирования 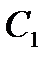и 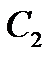вычислим производную от решения (13)

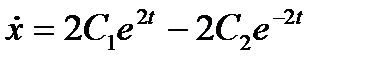(14)

и запишем начальные условия движения

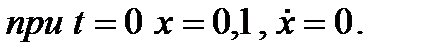
Подставляя эти начальные условия в (13) и (14), получим для нахождения 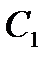и 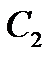систему уравнений

0,1= + ,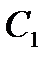

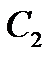0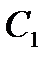=2 -2 .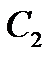

Решая эту систему уравнений, найдем 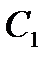= =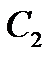0,05.

Окончательно закон движения шарика по трубке (13) примет вид

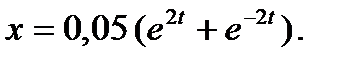(15)

Теперь с помощью выражения (15) можно получить ответ задачи. Обозначим 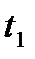момент вылета шарика из трубки. Тогда при t= 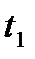x=l=1 м. Подставляя эти значения в (15), получим уравнение для нахождения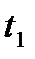

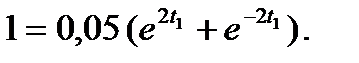
Решая это алгебраическое уравнение, найдем ответ задачи 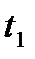≈1,5 с.