Метод математической индукции.

В основе метода математической индукции лежит принцип математической индукции.

Он заключается в следующем: некоторое утверждение справедливо для всякого натурального n, если

1. оно справедливо для n = 1 и Установлено, что верно. (Это утверждение называется базой индукции.)

2. из справедливости утверждения для какого-либо произвольного натурального n = k следует его справедливость для n = k+1 (Для любого n доказано, что если верно 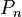, то верно . (Это утверждение называется индукционным переходом).

То есть, доказательство по методу математической индукции проводится в три этапа:

1. во-первых, проверятся справедливость утверждения для любого натурального числа n (обычно проверку делают для n = 1);

2. во-вторых, предполагается справедливость утверждения при любом натуральномn=k;

3. в-третьих, доказывается справедливость утверждения для числа n=k+1, отталкиваясь от предположения второго пункта.

Тогда все утверждения нашей последовательности верны.

Пример 3. Доказать, что для всех натуральных справедливо равенство

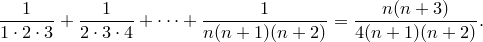
Обозначим через 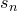левую часть равенства, а через 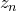— его правую часть.

1) Докажем сначала, что .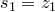

2) Дано: . Нужно доказать: .

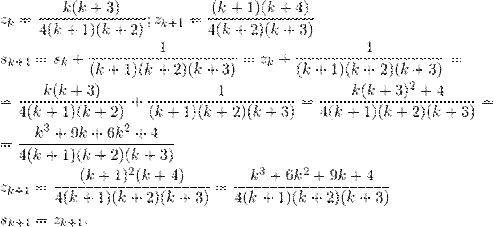
Тем самым, утверждение доказано для любого 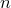, поскольку из его истинности для 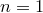следует, что оно истинно для 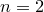, из его истинности при 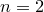следует его истинность для и т.д.

Задания для практического занятия:

Вариант 1

1. Используя методы доказательства:

- Прямым рассуждением докажите истинность высказывания: n и m — четные числа ® n+m — число четное.

- Дайте обратное доказательство высказывания: n² — четное число ® n — четное.

- Методом «от противного» докажите, что n+m — нечетное число ® одно из слагаемых является четным, а другое — нечетным.

2. Докажите методом математической индукции, что 1 + 5 + 9 +…+(4n - 3) = n(2n-1) для всех натуральных чисел n.

Вариант 2

1. Используя методы доказательства:

- Прямым рассуждением докажите истинность высказывания: n и m — четные числа ® n+m — число четное.

- Дайте обратное доказательство высказывания: n² — четное число ® n — четное.

- Методом «от противного» докажите, что n+m — нечетное число ® одно из слагаемых является четным, а другое — нечетным.

2. Докажите методом математической индукции, что 1²+2²+…+n² = n(n+1)(2n+1)/6 для всех натуральных чисел n.

Вариант 3

1. Используя методы доказательства:

- Прямым рассуждением докажите истинность высказывания: n и m — четные числа ® n+m — число четное.

- Дайте обратное доказательство высказывания: n² — четное число ® n — четное.

- Методом «от противного» докажите, что n+m — нечетное число ® одно из слагаемых является четным, а другое — нечетным.

2. Докажите методом математической индукции, что для всех натуральных чисел n.

Вариант 4

1. Используя методы доказательства:

- Прямым рассуждением докажите истинность высказывания: n и m — четные числа ® n+m — число четное.

- Дайте обратное доказательство высказывания: n² — четное число ® n — четное.

- Методом «от противного» докажите, что n+m — нечетное число ® одно из слагаемых является четным, а другое — нечетным.

2. Докажите методом математической индукции, что 1*1! + 2* 2!+…+-n*n! = (n + 1)! - 1 для всех натуральных чисел n.

Вариант 5

1. Используя методы доказательства:

- Прямым рассуждением докажите истинность высказывания: n и m — четные числа ® n+m — число четное.

- Дайте обратное доказательство высказывания: n² — четное число ® n — четное.

- Методом «от противного» докажите, что n+m — нечетное число ® одно из слагаемых является четным, а другое — нечетным.

2. Докажите методом математической индукции, что при каждом натуральном n число 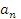делится на b: 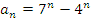, b=33

Контрольные вопросы:

1. В чем разница между доказательством прямым рассуждением, обратным, от противного?

2. Что означает математическая индукция? Объясните принцип математической индукции.

Практическая работа № 3

Метод математической индукции

Тема:«Основные понятия математической логики.»

Цель работы:изучить основы алгебры логики

Образовательные результаты:

Студент должен

уметь:

- формулировать задачи логического характера и применять средства математической логики для их решения.

знать:

- основные принципы математической логики, теории множеств и теории алгоритмов;

- формулы алгебры высказываний;

- методы минимизации алгебраических преобразований.

Оборудование: рабочая тетрадь, ручка, методические рекомендации по выполнению практической работы, справочная литература.

Методические указания по выполнению работы:

1. Ознакомиться с теоретическим материалом по практической работе.

2. Рассмотрите образцы решения задач по теме.

3.Выполнить предложенное задание согласно варианту по списку группы.

4.Изучить условие заданий для практической работы и выполнить её.

5. Ответить на контрольные вопросы даются письменно, после решения заданий в тетради для практических работ. Во время выполнения работы обучающийся может пользоваться своим конспектом, а также учебной литературой и справочным материалом.

5. Оформить отчет о работе. Сделайте вывод.