Важнейшие стандартные распределения
Дискретные распределения
Биномиальное распределение. Проведение эксперимента, в результате которого может произойти некоторое элементарное событие 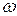 ,
, 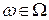 , назовем испытанием. Причем подразумевается, что эксперимент может быть повторен при неизменных условиях
, назовем испытанием. Причем подразумевается, что эксперимент может быть повторен при неизменных условиях  сколь угодно большое число раз. Два испытания будем называть независимыми, если вероятности произведения элементарных событий этих испытаний определяются по формуле
сколь угодно большое число раз. Два испытания будем называть независимыми, если вероятности произведения элементарных событий этих испытаний определяются по формуле 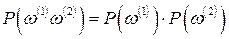 , где
, где 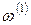 – элементарное событие первого испытания;
– элементарное событие первого испытания; 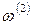 – элементарное событие второго испытания. Аналогично определяется независимость п испытаний, т.е. если для любого возможного результата п испытаний
– элементарное событие второго испытания. Аналогично определяется независимость п испытаний, т.е. если для любого возможного результата п испытаний 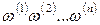 , где
, где 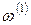 – результат первого испытания,
– результат первого испытания, 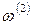 – результат второго испытания, …,
– результат второго испытания, …, 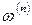 – результат п-го испытания, вероятность вычисляется по формуле
– результат п-го испытания, вероятность вычисляется по формуле
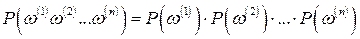 ,
,
то испытания назовем независимыми.
Остановимся на простейшем случае повторения одного и тогоже испытания при неизменных условиях, причем каждое испытание имеет два возможных исхода (два возможных элементарных события 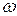 и
и 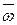 . Вероятность появления элементарного события
. Вероятность появления элементарного события 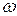 для каждого испытания постоянна и равна р, где 0 < р < 1. Такие испытания получили название схемы Бернулли.
для каждого испытания постоянна и равна р, где 0 < р < 1. Такие испытания получили название схемы Бернулли.
Биномиальное распределение является вероятностным законом последовательности независимых испытаний Бернулли.
Простейшей задачей, относящейся к испытаниям Бернулли, является отыскание вероятности Рп(т) того, что некоторое событие А наступит т раз при п испытаниях, а остальные п–т раз наступит противоположное событие 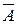 .
.
Для решения этой задачи введем случайную величину Х – число появлений события А в п независимых испытаниях. Эту случайную величину можно представить в виде суммы случайных величин Xi, где Xi – число появления события А в i-м испытании, т.е. 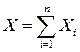 , причем множество значений каждой случайной величины
, причем множество значений каждой случайной величины 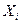 имеет вид:
имеет вид: 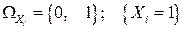 – событие А наступило в i-м испытании;
– событие А наступило в i-м испытании; 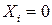 – событие А не наступило в i-м испытании. Предположим, что вероятность того, что событие А наступило в i-том испытании,
– событие А не наступило в i-м испытании. Предположим, что вероятность того, что событие А наступило в i-том испытании, 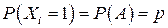 , а вероятность того, что событие А не наступило в i-том испытании,
, а вероятность того, что событие А не наступило в i-том испытании, 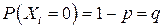 .
.
Пусть произведено п независимых испытаний. Результат каждого испытания будем отмечать буквой А, если событие А наступило, и буквой 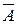 , если событие А не наступило. Предположим вначале, что событие А наступило в т первых испытаниях, а в остальных п–т испытаниях наступило событие
, если событие А не наступило. Предположим вначале, что событие А наступило в т первых испытаниях, а в остальных п–т испытаниях наступило событие 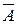 . Тогда по теореме умножения независимых событий вероятность этого результата п независимых испытаний равна
. Тогда по теореме умножения независимых событий вероятность этого результата п независимых испытаний равна 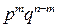 .
.
Но событие А может произойти в любых т испытаниях и число таких способов наступления события А т раз в п испытаниях будет равно числу сочетаний из п элементов по т, т. е. 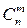 , и все результаты несовместны. Тогда, по теореме сложения вероятностей для несовместных событий, вероятность наступления события А т раз в п испытаниях равна
, и все результаты несовместны. Тогда, по теореме сложения вероятностей для несовместных событий, вероятность наступления события А т раз в п испытаниях равна 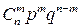 , т.е.
, т.е.
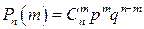 (2.11)
(2.11)
Формула (2.11) называется формулой Бернулли. Число сочетаний из 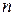 элементов по
элементов по 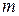 можно вычислить по формулам:
можно вычислить по формулам: 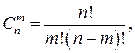 или
или 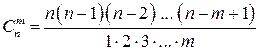 .
.
Появление события А т раз в п испытаниях, равносильно тому, что случайная величина Х приняла значение, равное т. Следовательно, случайная величина 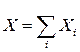 , являясь дискретной случайной величиной, принимает целочисленные значения от 0 до п и ее множество значений определяется множеством:
, являясь дискретной случайной величиной, принимает целочисленные значения от 0 до п и ее множество значений определяется множеством: 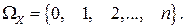 . Ряд распределения случайной величины Х имеет следующий вид:
. Ряд распределения случайной величины Х имеет следующий вид:
| хi | … | n | |||
| pi | 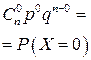 | 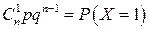 | 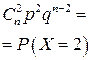 | … | 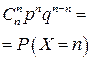 |
и называется биномиальным распределением, потому что вероятности 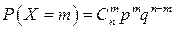 можно рассматривать как члены бинома (q+р)п.
можно рассматривать как члены бинома (q+р)п.
Функция F(х) дискретной случайной величины Х, распределенной по биномиальному закону, определяется формулой
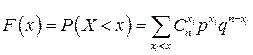 .
.
Числовые характеристики случайной величины Х – числа появлений события А в п независимых испытаниях — определяются достаточно просто. Покажем это.
Математическое ожидание числа появлений события А в п независимых испытаниях, т. е. случайной величины X, распределенной по биномиальному закону, равно произведению числа испытаний и вероятности появления события А в каждом испытании, т. е. М(Х) = пр.
Действительно, общее число Х появлений события А в п испытаниях складывается из числа появлений события в отдельных испытаниях Xi, 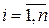 , т.е.
, т.е. 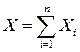 . Причем
. Причем 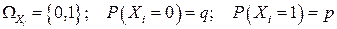 .
.
Поскольку математическое ожидание случайной величины Xi равно 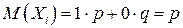 , то по свойству 4о математического ожидания
, то по свойству 4о математического ожидания 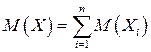 , получим:
, получим: 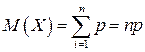 .
.
Дисперсия числа появлений события А в п независимых испытаниях, т, е. случайной величины X, распределенной по биномиальному закону, равна числу испытаний, умноженному на вероятности появления р и непоявления q события А в отдельном испытании, т.е. D(Х) = прq .
Докажем это. Как было показано выше, 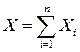 ,
, 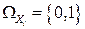 . В силу свойства 3° дисперсии
. В силу свойства 3° дисперсии 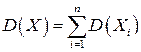 . Применим теорему 2.5
. Применим теорему 2.5 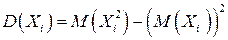 . Так как
. Так как 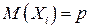 , то для вычисления
, то для вычисления 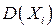 найдем
найдем 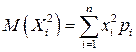 . Случайная величина
. Случайная величина 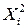 принимает значение либо 12 (событие А произошло в i-м испытании) с вероятностью р, либо 02 (событие А не произошло вi-м испытании) с вероятностью q= 1 – р. Поэтому
принимает значение либо 12 (событие А произошло в i-м испытании) с вероятностью р, либо 02 (событие А не произошло вi-м испытании) с вероятностью q= 1 – р. Поэтому 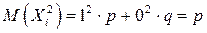 . Тогда
. Тогда 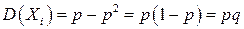 и
и 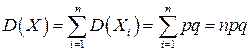 , что и требовалось доказать.
, что и требовалось доказать.
Пример 2.9.Пусть из большой партии изделий в целях контроля качества производится случайная выборка тридцати изделий с возвращением. Вероятность обнаружения брака р = 0,05. Вычислить вероятность того, что в случайной выборке: 1) нет бракованных изделий; 2) ровно 5 бракованных изделий.
Решение. Пусть Х – число бракованных изделий в выборке. Множество возможных значений случайной величины X: 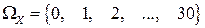 ;
;  -алгебру числового множества
-алгебру числового множества 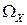 образуют любые подмножества
образуют любые подмножества 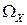 , в том числе и одноточечные:
, в том числе и одноточечные: 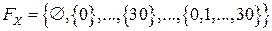 . Вероятности определим на элементарных событиях
. Вероятности определим на элементарных событиях 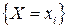 по формуле Бернулли:
по формуле Бернулли: 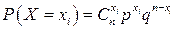 .
.
Пусть событие А состоит в том, что в выборке нет бракованных изделий, 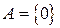 , а событие В состоит в том, что в выборке ровно 5 бракованных изделий, В= {5}. Их вероятности вычислим по формуле (2.11):
, а событие В состоит в том, что в выборке ровно 5 бракованных изделий, В= {5}. Их вероятности вычислим по формуле (2.11):
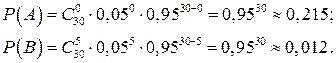
Ответ:вероятность того, что в случайной выборке: 1) нет бракованных изделий, равна 0,215; 2) ровно 5 бракованных изделий – 0,012.
Пример 2.10. Из партии изделий, изготовленных автоматом, для контроля качества производится случайная выборка 1000 изделий с возвращением. Пусть из эксперимента известно, что средний процент брака для данного автомата составляет 1%. Какова вероятность того, что среди 1000 отобранных изделий будет не более 3 дефектных?
Решение. Пусть случайная величина Х – число дефектных изделий. Множество ее возможных значений 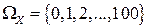 .
.  -алгебру образуют все возможные подмножества числового множества
-алгебру образуют все возможные подмножества числового множества 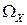 . Вероятности событий
. Вероятности событий 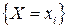 определим по формуле (1.11). Пусть событие А состоит в том, что среди отобранных изделий не более 3 дефектных, А = {0,1,2,3}, Так р=0,01, п=1000, то вероятность события А
определим по формуле (1.11). Пусть событие А состоит в том, что среди отобранных изделий не более 3 дефектных, А = {0,1,2,3}, Так р=0,01, п=1000, то вероятность события А
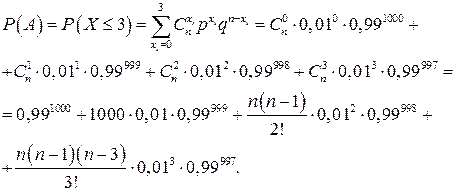
Ответ:вероятность того, что среди 1000 отобранных изделий будет не более 3 дефектных, равна 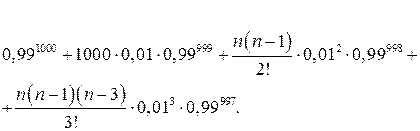
Из рассмотренного примера видно, что подсчет вероятностей по формуле Бернулли сопряжен в некоторых случаях с техническими трудностями. Поэтому необходимо получить приближенные формулы.
Наивероятнейшее число появления события в независимых испытаниях.Для получения приближенных формул вычисления вероятности появления события в независимых испытаниях исследуем изменение вероятностей 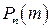 при различных значениях т. Рассмотрим отношение
при различных значениях т. Рассмотрим отношение
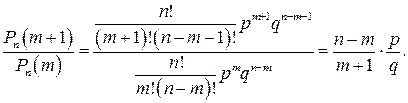
Тогда, если:
а) 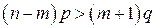 , т.е.
, т.е. 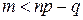 , то
, то 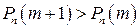 ;
;
б) 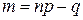 , то
, то 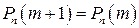 ;
;
в) 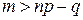 , то
, то 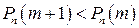 .
.
Таким образом, вероятность 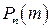 с ростом т вначале увеличивается, достигая максимума при некотором значении
с ростом т вначале увеличивается, достигая максимума при некотором значении 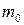 , а затем убывает. При этом, если np–q – целое число, то вероятность Рn (т) достигает максимума при двух значениях т:
, а затем убывает. При этом, если np–q – целое число, то вероятность Рn (т) достигает максимума при двух значениях т: 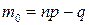 , и
, и 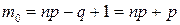 называемых наивероятнейшими значениями. Если же пр – q — не целое число, то наивероятнейшее значение одно, и оно удовлетворяет неравенству
называемых наивероятнейшими значениями. Если же пр – q — не целое число, то наивероятнейшее значение одно, и оно удовлетворяет неравенству
пр - q < т0 < nр+p,
так как вероятность максимальна при двух значениях т: т и т +1, те т 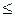 т0
т0 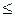 т+1. Объединяя это неравенство с равенствами, приведенными выше, получаем формулу
т+1. Объединяя это неравенство с равенствами, приведенными выше, получаем формулу
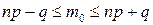 ,
,
по которой определяется наивероятнейшее число появления события в п независимых испытаниях.
Распределение Пуассона как предельное для биномиального. Как видно из примера 2.10, применение формулы Бернулли при малых р и больших п затруднительно. Однако значительный круг задач связан с необходимостью вычисления вероятностей Рп(т) именно при малых значениях р и больших п. Поэтому возникает задача отыскания асимптотической формулы, специально приспособленной для малых значений р. Такая формула была выведена Пуассоном.
Теорема 2.6. Если вероятность р появления события в каждом испытании, при неограниченном увеличении числа испытаний п, изменяется таким образом, что пр = а, а= соnst, то вероятность того, что некоторое событие появится т раз в п испытаниях стремится к величине

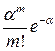 , т.е.
, т.е. 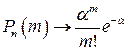 при
при  .
.
Доказательство. По формуле Бернулли
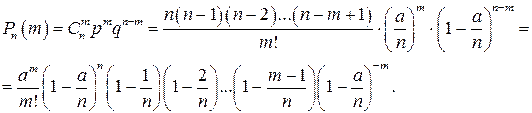
Так как при 
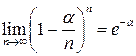 , а
, а
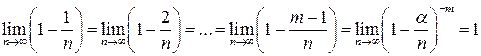 (α и т фиксированы), то
(α и т фиксированы), то 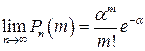 , что и требовалось доказать.
, что и требовалось доказать. 
Из теоремы следует, что для больших т и п справедливо равенство:
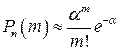 (2.12)
(2.12)
Предельную теорему Пуассона (формула (2.12)) используют, если р мало, а 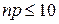 . Для удобства применения этой формулы составлены таблицы значений функции
. Для удобства применения этой формулы составлены таблицы значений функции 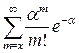 . Легко проверить, что
. Легко проверить, что 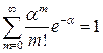 . Действительно,
. Действительно, 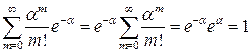 , так как ряд
, так как ряд 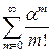 является экспоненциальным.
является экспоненциальным.
Рассмотрим далее дискретную случайную величину Х – число наступлений •бытия А в п независимых испытаниях, которая принимает значения 0, 1, …, т, … с вероятностями 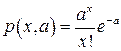 .
.
В этом случае говорят, что случайная величина Х распределена по закону Пуассона и, следовательно, ее ряд распределения имеет вид, представленный следующей таблицей:
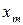 | … | т | … | |||
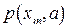 | 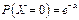 | 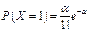 | 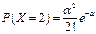 | … | 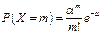 | … |
Как было показано выше, сумма вероятностей этого ряда распределения
равна 1. Функция пуассоновского распределения имеет вид
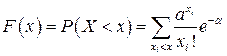 ;
;
Найдем числовые характеристики случайной величины Х. По определению математического ожидания
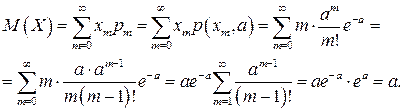
Таким образом, математическое ожидание числа появлений события А в п независимых испытаниях (случайная величина X) равно пр , а это параметр а. Дисперсия, согласно теореме 2.5,
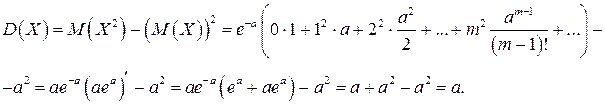 Дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию.
Дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию.
Асимметрия и эксцесс, как легко показать, соответственно равны: 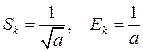 , откуда следует, что они всегда положительны.
, откуда следует, что они всегда положительны.
Пример 2.11. В тесто, приготовленное для выпечки 1000 булочек, засыпают 10000 изюминок и тщательно перемешивают. Какова вероятность того, что в случайно выбранной булочке будет: 1) 5 изюминок; 2) меньше 10 изюминок?
Решение. Пусть Х – число изюминок, попавших в булочку. Множество возможных значений случайной величины X: 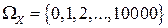 . В результате тщательного перемешивания каждая изюминка с одинаковой вероятностью может попасть в любую из 1000 булочек. Следовательно, вероятность того, что определенная изюминка попадает в выбранную булочку, равна 0,001. Число изюминок, попавших в выбранную булочку, можно рассматривать как результат п = 10 000 испытаний, в каждом из которых определенная изюминка с вероятностью р = 0,001 попадет в выбранную булочку. Так как пр = 10, то по теореме 2.6 вероятность события А =
. В результате тщательного перемешивания каждая изюминка с одинаковой вероятностью может попасть в любую из 1000 булочек. Следовательно, вероятность того, что определенная изюминка попадает в выбранную булочку, равна 0,001. Число изюминок, попавших в выбранную булочку, можно рассматривать как результат п = 10 000 испытаний, в каждом из которых определенная изюминка с вероятностью р = 0,001 попадет в выбранную булочку. Так как пр = 10, то по теореме 2.6 вероятность события А =  число изюминок в случайно выбранной булочке равна 5
число изюминок в случайно выбранной булочке равна 5 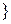 , будет равна:
, будет равна:
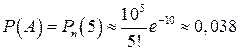 .
.
Вероятность события В =  число изюминок в случайно выбранной булочке меньше 10
число изюминок в случайно выбранной булочке меньше 10 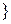 , вычислим, используя формулу (2.12)
, вычислим, используя формулу (2.12)
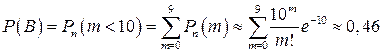 .
.
Ответ:вероятность того, что в случайно выбранной булочке будет: 1) 5 изюминок, равна 0,038; 2) меньше 10 изюминок – 0,46.
Примерами случайных величин, подчиняющихся закону распределения Пуассона, могут служить:
- количество распадающихся за короткий промежуток времени атомов радиоактивного вещества;
- число обрывов нити определенного сорта пряжи в течение времени Т;
- число дефектов в куске ткани определенной длины;
- число зафиксированных за определенный период времени метеоритов и т. д.
Простейший поток событий и его математическая модель. Формулу (2.12) можно считать математической моделью простейшего потока событий.
Введем некоторые определения.
Определение 2.15. Потоком событий называется последовательность событий, которые наступают в случайные моменты времени.
Например, поступление вызовов на станцию "Скорой помощи", моменты прибытия судов в порты, и т.д.
Определение 2.16.Простейшим (пуассоновским) потоком событий называется поток событий, обладающий свойствами:
а) стационарности (вероятность появления т событий на любом промежутке времени зависит только от числа т событий и от длительности t промежутка времени и не зависит от начала и конца отсчета времени);
б) отсутствия последействия (вероятность появления событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка):
в) ординарности (появление двух или более событий за малый промежуток времени практически невозможно).
Определение 2.17. Интенсивностью потока λ называется среднее число событий, которые появляются в единицу времени.
Тогда, если постоянная λ интенсивности потока известна, то вероятность появления т событий простейшего потока за время t определяется по формуле Пуассона:
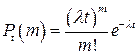 . (2.13)
. (2.13)
Эта формула отражает все свойства простейшего потока событий:
· вероятность появления т событий за время t при заданной интенсивности является только функцией т и t, т. е. обладает свойством стационарности;
· в формуле (2.13) не используется информация о появлении событии до начала рассматриваемого промежутка, т.е. обладает свойством отсутствия последствия;
· формула (2.13) обладает свойством ординарности, так как сравнивая вероятности:
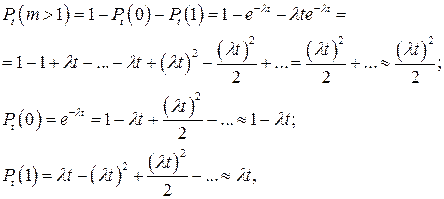
замечаем, что при малом t вероятность появления более одного события гораздо меньше, чем вероятность появления одного события.
Простейший поток событий образуют вызовы, поступающие на автоматическую телефонную станцию. Если средняя плотность вызовов в час равна λ, то вероятность поступления вызовов за время t определяется по формуле (2.13).
Пример 2.12. Пусть известна интенсивность числа телефонных вызовов λ, равная 4. Предполагая, что телефонные вызовы независимы и равномерно распределены в течение определенного интервала времени, определить вероятность того, что в минуту зарегистрируется не более двух вызовов.
Решение. Пусть случайная величина Х - число телефонных вызовов. Так как телефонные вызовы образуют простейший поток событий, то искомая вероятность, согласно формуле (2.13), будет равна
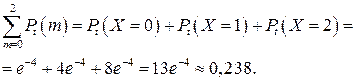
Ответ:вероятность того, что в минуту зарегистрируется не более двух вызовов, равна 0,238.
Пример 2.13. Назовем неисправность в работе ЭВМ сбоем. Будем считать поток сбоев ЭВМ простейшим потоком событий. Пусть интенсивность этого потока за сутки равна 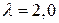 . Найти вероятности того, что: 1) в течение суток не будет ни одного сбоя; 2) в течение суток произойдет хотя бы один сбой.
. Найти вероятности того, что: 1) в течение суток не будет ни одного сбоя; 2) в течение суток произойдет хотя бы один сбой.
Решение. Рассмотрим случайную величину Х – число сбоев ЭВМ за время работы. Так как поток сбоев считаем простейшим, то вероятность того, чтоза некоторое время работы произойдет хi, сбоев, вычислим по формуле (2.13):
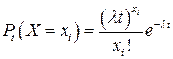 , где λ= 2.
, где λ= 2.
Тогда вероятность того, что в течение суток не будет ни одного сбоя ЭВМ будет равна
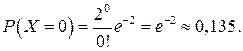
Событие, состоящее в том, что в течение суток произойдет хотя бы один сбой 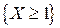 , противоположно событию
, противоположно событию 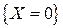 . Поэтому его вероятность определим по формуле
. Поэтому его вероятность определим по формуле
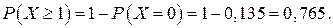
Ответ:вероятности того, что: 1) в течение суток не будет ни одного сбоя, равна 0,135; 2) в течение суток произойдет хотя бы один сбой – 0,765.
Геометрическое распределение. Геометрическое распределение представляет собой распределение случайной величины Х – число независимых экспериментов, которые нужно выполнить до первого появления события А. Ряд распределения случайной величины Х имеет вид
| xi | … | m | … | |||
| pi | p | qp | q2p | … | qm-1p | … |
Математическое ожидание по определению вычисляется по формуле
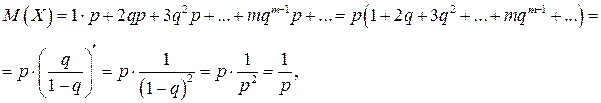
так как
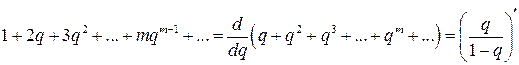
Дисперсию вычислим, используя теорему по теорему 2.5
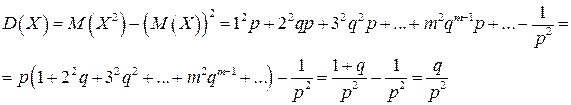 так как
так как
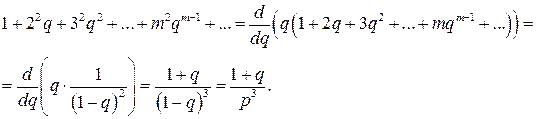 Среднее квадратическое отклонение
Среднее квадратическое отклонение
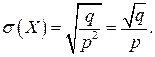
Пример 2.14. Производятся ряд попыток запуска двигателя, каждая попытка длительностыо 10с заканчивается запуском двигателя независимо от других с вероятностью р=0,8. Найти распределение общего времени Т, которое требуется для запуска двигателя. Вычислить математическое ожидание и среднее квадратическое отклонение случайной величины – времени Т, необходимого для запуска двигателя.
Решение. Введем случайную величину Х – число попыток запуска двигателя, которая распределена по геометрическому закону. Общее время Т, необходимое для запуска двигателя, связано со случайной величиной Х формулой Т = Хt, где t = 10с и имеет распределение вида
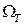 | t | 2t | 3t | … | mt | … |
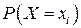 | p | qp | q2p | … | qm-1p | … |
Математическое ожидание и среднее квадратическое отклонение случайной величины T будут равны:
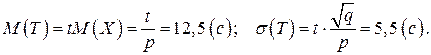
Ответ:математическое ожидание и среднее квадратическое отклонение случайной величины – времени Т, необходимого для запуска двигателя, соответственно равны 12,5с и 5,5с.
Гипергеометрическое распределение. Это распределение используется при контроле качества продукции для оценки доли бракованных изделий в выборке из контролируемой партии.
Пусть каждыйиз N объектов некоторой совокупности обладает одним из двух признаков 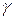 и
и 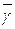 , причем признаком
, причем признаком 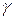 обладает М объектов, а признаком
обладает М объектов, а признаком 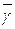 – (N – М) объектов. Число М и частость
– (N – М) объектов. Число М и частость 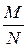 объектов, обладающих признаком
объектов, обладающих признаком 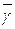 , неизвестны. Для оценки частости
, неизвестны. Для оценки частости 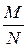 отбираем п обьектов, и пусть т– число объектов, обладающих признаком
отбираем п обьектов, и пусть т– число объектов, обладающих признаком 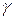 в выборке, состоящей из п объектов. Рассмотрим случайную величину Х — число объектов в выборке, обладающих признаком
в выборке, состоящей из п объектов. Рассмотрим случайную величину Х — число объектов в выборке, обладающих признаком 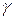 . Вычислим вероятность того, что случайная величина приняла значение т. Число выборок по п объектов из N будет определяться числом сочетаний
. Вычислим вероятность того, что случайная величина приняла значение т. Число выборок по п объектов из N будет определяться числом сочетаний 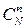 , так как выборки будут различны, если они отличаются хотя бы одним объектом. Среди указанных выборок (их число
, так как выборки будут различны, если они отличаются хотя бы одним объектом. Среди указанных выборок (их число 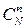 ) будет
) будет 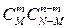 , содержащих т объектов с признаком
, содержащих т объектов с признаком 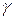 . Тогда на основании классического определения вероятности событий {X=m} искомая вероятность того, что случайная величина Х примет значение, равное т ,
. Тогда на основании классического определения вероятности событий {X=m} искомая вероятность того, что случайная величина Х примет значение, равное т ,
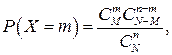 (2.14)
(2.14)
где т принимает целочисленные значения 0,1,2,..., min(п, М). Функция распределения дискретной случайной величины Х имеет вид
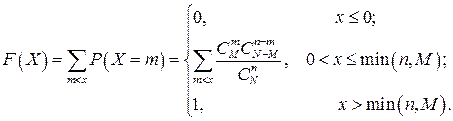 (2.15)
(2.15)
Причем 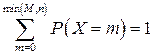 . Дискретное распределение с функцией распределения (2.15) называется гипергеометрическим.
. Дискретное распределение с функцией распределения (2.15) называется гипергеометрическим.
Формулу (2.14) для различных значений т можно записать в виде
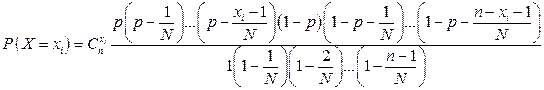 ,(2.16)
,(2.16)
где 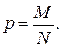
Из формулы видно, что распределение дискретной случайной величины Х зависит от трех параметров: п , р и N . Из формулы (2.16) следует, что при N стремящемся к бесконечности и при 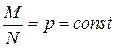 получим
получим
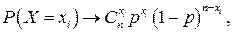
т.е. члены гипергеометрического распределения стремятся к соответствующим членам биномиального распределения.
По формулам (2.7) и (2.10) вычислим математическое ожидание и дисперсию гипергеометрического распределения:
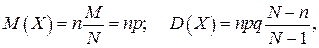
где 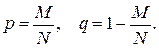
Пример 2.15. Из партии, содержащей 500 изделий, для проверки качества отбирается случайным образом 3 изделия. Известно, что для данных изделий брак составляет 2%. Определить вероятность того, что среди 3 отобранных изделийнет бракованных.
Решение. Пусть случайная величина Х – число бракованных изделий, содержащихся в выборке. Множество возможных значений 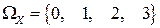 . Вероятность события {Х = 0}, состоящего в том, что среди отобранных изделий нет бракованных, вычислим по формуле (2.14), где N=500; n= 3;
. Вероятность события {Х = 0}, состоящего в том, что среди отобранных изделий нет бракованных, вычислим по формуле (2.14), где N=500; n= 3; 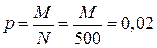 ; т = 0. Определим М= 500•0,02= 10. Тогда,
; т = 0. Определим М= 500•0,02= 10. Тогда,
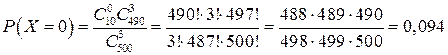 .
.
Ответ:вероятность того, что среди 3 отобранных изделийнет бракованных, равна 0,094.
Вопросы для самопроверки
1. Что характеризует случайная величина 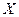 , которая подчиняется биномиальному закону (закону Бернулли) распределения?
, которая подчиняется биномиальному закону (закону Бернулли) распределения?
2. Какие значения может принимать случайная величина 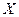 , которая подчиняется биномиальному закону распределения?
, которая подчиняется биномиальному закону распределения?
3. Выпишите формулу для вычисления функции распределения случайной величины 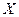 , которая подчиняется биномиальному закону распределения?
, которая подчиняется биномиальному закону распределения?
4. Выпишите формулы для вычисления числовых характеристик случайной величины 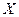 , которая подчиняется биномиальному закону распределения?
, которая подчиняется биномиальному закону распределения?
5. В каких пределах изменяется наивероятнейшее число появления события в независимых испытаниях?
6. В каких случаях применяется предельная теорема Пуассона?
7. Какие значения может принимать случайная величина 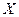 , которая подчиняется закону распределения Пуассона?
, которая подчиняется закону распределения Пуассона?
8. Чему равна дисперсия случайной величины 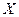 , распределенной по закону Пуассона?
, распределенной по закону Пуассона?
9. Какую формулу можно считать математической моделью простейшего потока событий и почему?
10. Что характеризует случайная величина 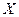 , распределенная по геометрическому закону?
, распределенная по геометрическому закону?
11. Какое распределение используется для контроля качества продукции?
Непрерывные распределения
Равномерное (прямоугольное) распределение. Пусть плотность вероятности равна нулю всюду, кроме отрезка [α; β], на котором все значения случайной величины Х одинаково возможны. Напишем выражение плотности распределения вероятностей р(х). Для этого обозначим постоянную плотность на [α; β] через А=const , тогда
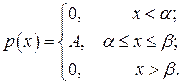
Так как площадь, ограниченная кривой распределения, (как площадь прямоугольника) равна единице:
А(β – α) = 1 (рис. 2.14), то 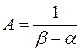 , и плотность распределения р(х) примеет вид
, и плотность распределения р(х) примеет вид
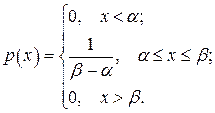 (2.17)
(2.17)
Отрезок [α; β] называется отрезком концентрации равномерного распределения.
График плотности вероятностей равномерного распределения приведен на рис. 2.14.
Формула (2.17) и выражает закон равномерной плотности на отрезке [α; β]. Найдем функцию распределения F(х), учитывая, что
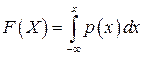
В зависимости от местоположения действительного числа х, рассмотрим 3 случая:
а) Пусть х<α , тогда 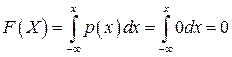 .
.
б) Если же 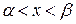 , то
, то
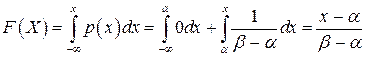 .
.
в) При  получим
получим
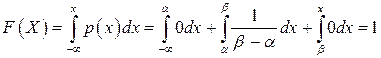 .
.

Рис.2.14 Рис.2.15
