Правила вычисления производных

Производная сложной функции.

Если у=ƒ(и), и=φ(х), то у¢(х)=ƒ¢(и)·φ¢ (х).

Производная суммы.

Если у(х)=и(х)+v (х), то у¢ (х)=и¢ (х)+v¢ (х)

Производная произведения.

Если у(х)=и(х)·v(х), то у¢=и¢·v+u·v¢.

В частности, (с·и)¢=с·и¢, т. е. постоянный множитель выносится из-под знака производной. Легко убедиться, что

(u²)¢=2u·u¢, (u³)¢=3u²·u¢, … , (uⁿ)¢=n·u^n–1·u¢.

Производная частного. Если 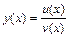, то .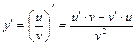

Приведем и таблицу производных:

1. (с)¢=0	Для сложной функции: если и=и(х), то:
2. (х)¢=1
3. (хα)¢=α·хα–1, а – любое действительное число. 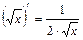.	3.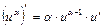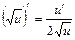
4. (ах)¢=ах·ln а	4.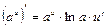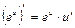
5. (logax)¢= 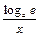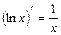.	5.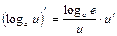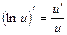
6. (sin x)¢=cos x	6.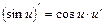
7. (cos x)¢= –sin x	7.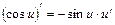
8. (tg x)¢=	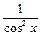8.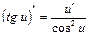
9. (ctg x)¢=	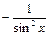9.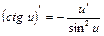
10.	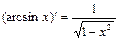10.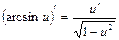
11.	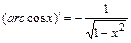11.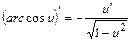
12.	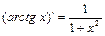12.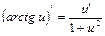
13.	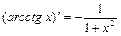13.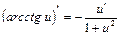

При дифференцировании следующих функций укажем формулы и правила, которыми будем пользоваться.

Найти производные следующих функций.

Пример 1.

у=(3–2 sin5x)⁴ |Применяем формулы производных для и^α, sin u|

y¢=4·(3–2·sin5x)³·(3–2sin5x)¢=4·(3–2·sin5x)³·(0–2·cos5x·5) = –40·(3–2·sin5x)³.

Пример 2.

.

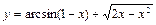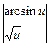
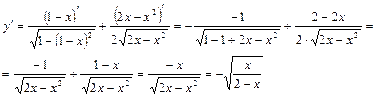
Пример 3.

.

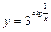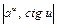
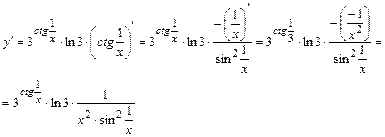
Пример 4.

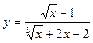
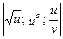
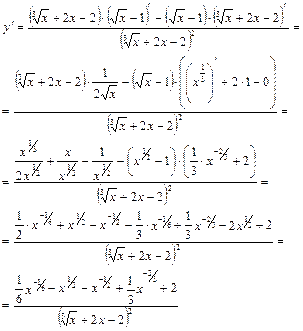
Пример 5.

.

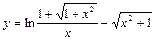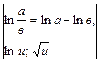
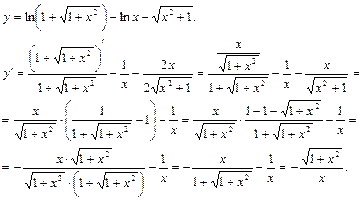
Пример 6.

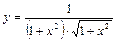Запишем функцию так, чтобы упростить процесс дифференцирования

.

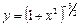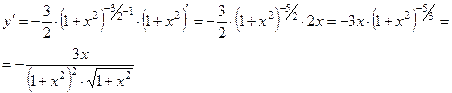
Пример 7.

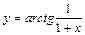
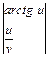
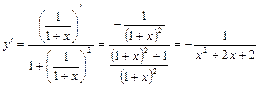
Пример 8.

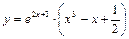
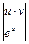
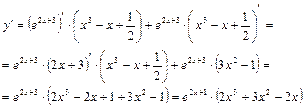
Пример 9.

.

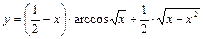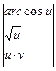
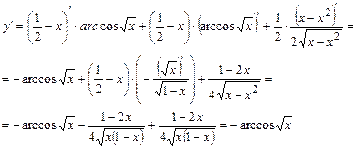
Пример 10.

Составить уравнение касательной к параболе у=х²–4х в точке, где х=1.

Уравнение касательной у-у₀=ƒ¢(х₀)·(х–х₀), где х₀, у₀ – координаты точки касания.

Дано, что х₀=1. Из уравнения параболы найдем у₀=у(х₀)=у(1)=1²–4·1= –3.

Уравнение параболы у=х²–4х, т. е. ƒ(х)=х²–4х. Найдем ƒ¢(х₀).

ƒ¢(х)=2х–4. ƒ¢(х₀)=ƒ¢(1)=2·1–4= –2.

Уравнение касательной:

у+3= –2·(х–1) или 2х+у+1=0

Пример 11.

Дана кривая 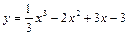. Составить уравнения касательных к этой кривой, параллельных

а) оси Ох, б) прямой3х–у–5=0.

Найдем производную от у:

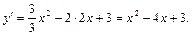
а) Если касательная параллельна оси Ох, то угловой коэффициент ее равен нулю, т. е. производная в точке х₀ должна быть равна нулю: х²–4х+3=0. Решая это уравнение, находим х₁=3 и х₂=1. Найдем соответствующие им значения функции:

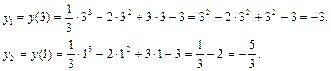
Получены две точки на данной кривой: М₁(3, –3) и М₂(1, ).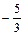

Касательные – прямые, проходящие параллельно оси Ох, имеют уравнения: у= –3 и у= .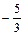

б) Если касательная параллельна прямой 3х-у-5=0, то ее угловой коэффициент равен угловому коэффициенту данной прямой:

3х–у–5=0 или у=3х–5.

k=3.

Производная у¢ в точке х₀ должна быть равна 3.

х²–4х+3=3. Решая это уравнение х²–4х=0, находим х₁=0 и х₂=4.

Найдем соответствующие им значения функции:

у₁=у(0)= –3. у₂=у(4)= 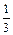·4³–2·4²+3·4–3= – .

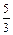Уравнение касательной в точке М₁(0,–3):

у+3=3·(х–0) или 3х–у–3=0.

Уравнение касательной в точке М₂(4, – ):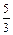

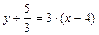или 9х–3у–41=0.

Дифференциал функции

Пусть функция у=ƒ(х) определена на множества Х и дифференцируема в каждой его точке.

Определение. Дифференциалом функции называется произведение

производной функции на приращение аргумента и

обозначается dy или dƒ(х), т. е.

dy=ƒ¢(x)·Δx

Пусть дана функция у=х. Тогда у¢=1. Дифференциал этой функции dy=1·Δx, т.е. dx=Δx.

Поэтому формулу дифференциала записывают в виде

dy=f¢(x)·dx

Отсюда 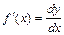, т. е. производная есть отношение дифференциалов функции и аргумента. Иногда удобно пользоваться именно таким «определением» производной.

Производные высших порядков

Если функция у=ƒ(х) имеет производную ƒ¢(х), которая, вообще говоря, сама является дифференцируемой функцией, то производная от ƒ¢(х) называется производной второго порядка (или второй производной) от функции ƒ(х) и обозначается: у^и, ƒ¢¢(х), т. е.

ƒ¢¢(х)=(ƒ¢(х))¢.

Аналогично, производной третьего порядка (третьей производной) от функции ƒ(х) называется производная от второй производной ƒ¢¢(х), т. е.

ƒ¢¢¢(х)=(ƒ¢¢(х))¢.

Производная четвертого порядка

ƒ^IV(х)=(ƒ¢¢¢(х))¢.

Например, для функции

ƒ(х)=2х⁶–sin3x

ƒ¢(x)=12x⁵–3cos3x,

ƒ¢¢(x)=12·5x⁴–3·(–sin3x)·3=60x⁴+9sin3x,

ƒ¢¢¢(x)=60·4x³+9·cos3x·3=240x³+27cos3x,

ƒ^IV(x)=240·3x²–27sin3x·3=720x²–81sin3x и т. д.

Производную порядка n обозначают:

y⁽ⁿ⁾ или ƒ⁽ⁿ⁾(x).