Численное решение обыкновенных дифференциальных уравнений

Краткое введение.Дифференциальное уравнение первого порядка ,разрешенное относительно производной , имеет вид

y ^' = f (x ,y ). (1)

Решением дифференциального уравнения (1) называется функция φ ( x ), подстановка которой в уравнение обращает его в тождество : φ ^' ( x ) ₌ f (x , φ ( x ) ) . График решения y = φ ( x )называется интегральной кривой.

Задача Кошидля дифференциального уравнения (1) состоит в том , чтобы найти решение уравнения (1) , удовлетворяющему начальному условию

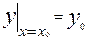(2)

пару чисел ( x₀ , y₀ ) называют начальными данными . Решение задачи Коши называется частным решениемуравнения ( 1 ) при условии ( 2 ) .

Численное решение задачи Коши ( 1 ) - ( 2 ) состоит в том , чтобы получить искомое решение φ ( x )в виде таблицы его приближенных решений для заданных значений аргумента xна некотором отрезке [ a , b ]:

X₀ = a , x ₁ , x ₂ , . . . , x _m = b ( 3 )

Точки (3) называются узловыми точками, а множество этих точек называется сеткойна отрезке [ a , b ] . Будем использовать равномерную сетку с шагом h :

h = ( b - a ) / m ; x _i - x _{i - 1} = h или x _i = x ₀ + ih ( i = 1 , . . . , m ) .

Приближенные значения численного решения задачи Коши в узловых точках x _i обозначим через y _i ; таким образом ,

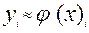( i = 1 , . . . , m ) .

Для любого численного метода решения задачи ( 1 ) - ( 2 ) начальное условие ( 2 ) выполняется точно , т . е . .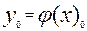

Величина погрешности численного метода решения задачи Коши на сетке отрезка

[ a , b ] оценивается величиной

,

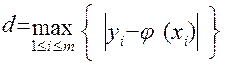Говорят , что численный метод имеет p- й порядок точности по шагу h на сетке , если расстояние d можно представить в виде степенной функции от h :

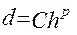, p > 0 ,

где c - некоторая положительная постоянная , зависящая от правой части уравнения (1) и от рассматриваемого метода . В данном случае очевидно , что когда шаг h стремится к нулю , погрешность d также стремится к нулю .

Метод Эйлера.Простейшим численным методом решения задачи Коши ( 1 ) - ( 2 ) является метод Эйлера.

Угловой коэффициент касательной к интегральной кривой в точке P₀ ( x₀ , y₀ ) есть

y ^'₀ = f (x₀ ,y₀ ).

Найдем ординату y₁ касательной , соответствующей абсциссе x ₁ = x ₀ + h . Так как уравнение касательной к кривой в точке P ₀ имеет вид y - y₀ = y ^' ( x - x₀ ) , то

y₁ = y₀ + h f (x₀ , y₀ ).

Угловой коэффициент в точке P₁ (x₁ ,y₁) также находится из данного дифференциального уравнения y^'₁ = f(x₁,y₁). На следующем шаге получаем новую точку P₂ (x₂ ,y₂) , причем

x₂ = x₁ + h , y₂ = y₁ + hf(x₁ ,y₁) .

Продолжая вычисления в соответствии с намеченной схемой , получим формулы Эйлерадля m приближенных значений решения задачи Коши с начальными данными (x₀ , y₀) на сетке отрезка [ a , b ] с шагом h:

x_i = x_{i -1} + h , y_i = y_{i - 1} + hf(x_{i - 1} , y_{i - 1} ) ( i = 1,2 , . . . , m ) (4)

Графической иллюстрацией приближенного решения является ломаная , соединяющая последовательно точки P₀ , P₁, P₂, . . . ,P_m , которую называют ломаной Эйлера .

Погрешность метода Эйлера можно оценить неравенством

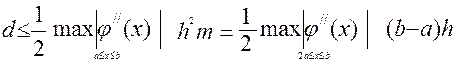
или представить в ви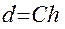де

, где .

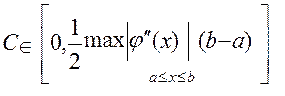Это означает , что метод Эйлера имеет первый порядок точности . В частности , при уменьшении шага h в 10 раз погрешность уменьшится примерно в 10 раз.

Практическую оценку погрешности решения , найденного на сетке с шагом h/2 , в точке 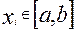производят с помощью приближенного равенства - правила Рунге:

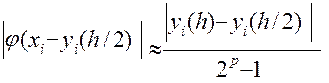,(5)

где p - порядок точности численного метода. Таким образом , оценка полученного результата по формуле (5) вынуждает проводить вычисления дважды : один раз с шагом h , другой - с шагом h/2 .

Методы Рунге - Кутта.Численные методы решения задачи Коши

,

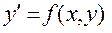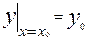
на равномерной сетке { x₀ = a , x₁ , x₂ , . . . ,x_m = b}отрезка[ a, b ]с шагом

h = ( b -a) /m являются методами Рунге - Кутта , если , начиная с данных (x_{0 ,}y₀ ), решение ведется по следующим рекуррентным формулам

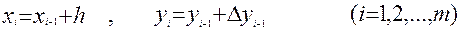(6)

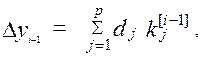
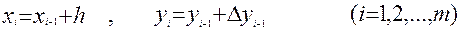
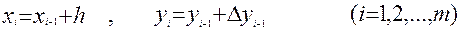
Метод называют методом Рунге - Кутта порядка p ,если он имеет p - й порядок точности по шагу h на сетке .Порядок точности p достигается с помощью формул (6) при определенных значениях коэффициентов c_j и d_j ( j = 1,2, . . . ,p); c₁ всегда полагают равным нулю.

Метод Рунге - Кутта второго порядка называют методом Эйлера - Коши , если p = 2 ,

c₁ = 0 , c₂ = 1 , d₁ = d₂ = 1/2. Алгоритм Эйлера - Коши получается из формул (6):

x_i =x_i-1 + h, y_i = y_i-1 + Δy_i-1, Δy_i-1 = (1/2)[ k₁^{[i -1]} + k₂^{[i -1]}] ( i = 1, ..., m), (7)

k₁^{[ i - 1]} = hf ( x_i-1,y_i-1), k₂^{[ i - 1 ]} = hf ( x_i-1 + h , y_i-1 + hf ( x_i-1 ,y_i-1) )

Для практической оценки погрешности решения можно применять правило Рунге, полагая в формуле (5) р = 2.

Метод Рунге - Кутта четвертого порядка называют классическим методом Рунге - Кутта, если p = 4 , c₁ = 0 , c₂ = c₃ = 1/2 , c₄ = 1 , d₁ = d₄ = 1/6 , d₂ = d₃ =1/3.

Из рекуррентных формул (6)получим алгоритм решения задачи Коши классическим методом Рунге - Кутта :

x _I = x _i - ₁ + h , y _i = y _{i - 1} + Δy _{i – 1} ( i = 1,2, . . . , m) ,

Δy_i-1 = 1/6 [ k₁^{[ i - 1]} + 2 k₂^{[ i - 1]} + 2k₃^{[ i - 1]} + k₄^{[ i - 1]} ] ,

k₁^{[ i - 1]} = h f ( x_{i - 1 ,} y_{i -1}) ,

k₂^{[ i - 1 ]} = h f( x_{i - 1} + (1/2) h , y _{i - 1} + (1/2)k₁^{[ i - 1 ]} ) ,

k₃^{[ i - 1]} = h f ( x_i - ₁ + (1/2)h , y _{i - 1} + (1/2)k₂^{[ i - 1 ]} ) ,

k₄^{[ i - 1 ]} = h f( x_{i - 1} + h , y _{i - 1} + k₃^{[ i - 1 ]} ) ,

Графиком приближенного решения является ломаная , последовательно соединяющая точки

P_i( x_i , y_i) ( i = 0 , 1 , 2, . . ., m). С увеличением порядка численного метода звенья ломаной приближаются к ломаной , образованной хордами интегральной кривой y = φ(x) , последовательно соединяющими точки ( x_i , φ(x_i) ) на интегральной кривой .

Правило Рунге (5) практической оценки погрешности решения для численного метода четвертого порядка имеет вид

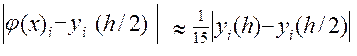
Задание на работу .

Решить задачу Коши на равномерной сетке. Решение найти в четырех узловых точках

( шаг h₁ равен [ b - a ] / 4 ) . Найти решение в тех же узлах, ведя расчет с уменьшенным вдвое шагом. Вычислить погрешности приближений при расчете с шагом h₂ = h₁ / 2

Задачу решить :

а) методом Эйлера ;

б) методом Эйлера - Коши ;

в) методом Рунге - Кутта .

Варианты лабораторных работ.

1.

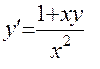
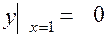
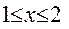
2.

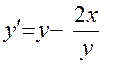
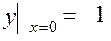
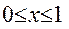
3.

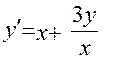
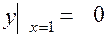
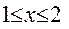
4.

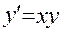
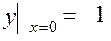
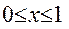
5.

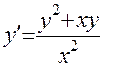
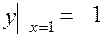
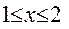
6.

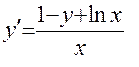
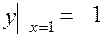
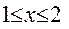
7.

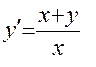
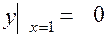
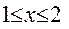
8.

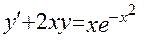
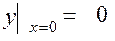
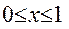
9.

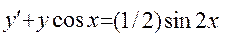
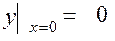
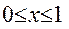
10.

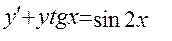
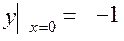
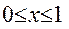
11.

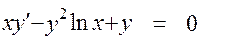
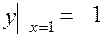
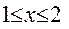
12.

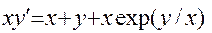
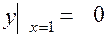
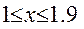
13.

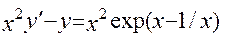
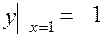
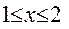
14.

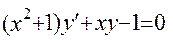
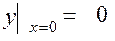
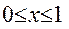
15.

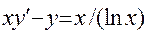
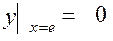
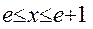
16.

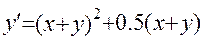
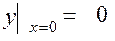
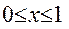
17.

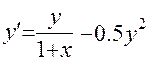
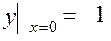
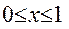
18.

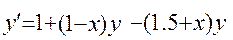
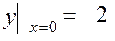
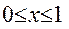
19.

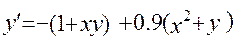
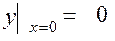
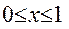
20.

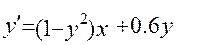
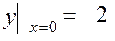
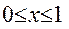
Вспомогательные материалы.

Пример

Решить задачу Коши

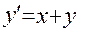
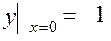
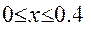
на равномерной сетке с шагом h = 0.1 . Решение найти в четырех узловых точках .

С помощью программы найти решение в тех же узлах, ведя расчет с уменьшенным вдвое шагом. Вычислить погрешности приближений при расчете с шагом h = 0.05

Задачу решить :

а) методом Эйлера ;

б) методом Эйлера - Коши ;

в) методом Рунге - Кутта .

Решение. Здесь f ( x,y) = x + y ; m = 4 ; a = 0 ; b = 0.4 ;

h = ( b - a ) / m = 0.4 /4 = 0.1

а) Используя рекуррентные формулы

x₀ = 0 ; y₀ = 1; x_i = x _{i - 1} + 0.1; y _i = y _{i - 1} + 0.1( x _{i - 1} + y _{i - 1} ) i = ( 1, 2, 3, 4 ) ,

последовательно находим

при i = 1 : x₁ = 0.1 ; y₁ = 1 + 0.1( 0 + 1 ) = 1.1 ;

при i = 2 ; x₂ = 0.2 ; y₂ = 1.1 + 0.1( 0.1 + 1.1 ) = 1.22 ;

при i = 3 ; x₃ = 0.3 ; y₃ = 1.22 + 0.1( 0.2 + 1.22 ) = 1.362 ;

при i = 4 ; x₄ = 0.4 ; y₄ = 1.362 + 0.1( 0.3 + 1.362 ) = 1.5282.

С помощью программы находим решение при h = 0.05 .

Обозначив , d _i = | y _i ( h ) - y _i ( h/2) | сведем результаты вычислений в таблицу

I	x i	y i ( h )	y i ( h / 2)	d
	0.1	1.1	1.105	0.005
	0.2	1.22	1.231012	0.011012
	0.3	1.362	1.380119	0.018191
	0.4	1.5282	1.554911	0.028738

б) Формулы ( 7) в нашем случае принимают вид

k₁^{[ i - 1]} = h ( x_i-1 + y_i-1), k₂^{[ i - 1 ]} = h ( x_i-1 + h + y_i-1 + k₁^{[ i - 1]})

x_i =x_i-1 + h , y_i = y_i-1 + (1/2)[ k₁^{[i -1]} + k₂^{[i -1]}] ( i = 1, 2 , 3 , 4) .

Полагая x ₀ = 0 , y ₀ = 1 , последовательно находим

при i = 1 :

k₁^{[ 0 ]} =0.1( 0 + 1 ) = 0.1 ; k₂^{[ 0 ]} = 0.1( 0 + 0.1 + 1 + 0.1) = 0.12 ;

x₁= 0 + 0.1 = 0.1 ; y₁ = 1 + ( 1/2 )( 0.1 + 0.12 ) = 1.11 ;

при i = 2 :

k₁^{[ 1 ]} =0.1( 0.1 + 1.11 ) = 0.121 ; k₂^{[ 1 ]} = 0.1( 0.1+0.1+1.11+0.121) = 0.1431 ;

x₁= 0.1 + 0.1 = 0.2 ; y₁ = 1.11+(1/2)(0.121+0.143) = 1.2425 .

Далее получаем при i = 3 : x ₃ = 0.3 _; y ₃ = 1.398465 ;

При i = 4 : x ₄ = 0.4 _; y ₄ = 1.581804 .

С помощью программы проводим вычисления с половинным шагом . Результаты заносим в таблицу , аналогичную таблице пункта а) .

в) Из формул (8 ) получаем

k₁^{[ i - 1]} = h ( x_i-1 + y_i-1), k₂^{[ i - 1 ]} = h ( x_i-1 + (1/2)h + y_i-1 +(1/2) k₁^{[ i - 1]})

k₃^{[ i - 1 ]} = h ( x_i-1 + (1/2)h + y_i-1 +(1/2) k₂^{[ i - 1]})

k₄^{[ i - 1 ]} = h ( x_i-1 + h + y_i-1 + k₃^{[ i - 1]})

x_i =x_i-1 + h , y_i = y_i-1 + (1/6)[ k₁^{[i -1]} + 2k₂^{[i -1]} + 2k₃^{[i -1]} + k₄^{[ i - 1 ]}]

для i = 1, 2 , 3 , 4 .

Полагая x ₀ = 0 , y ₀ = 1 , последовательно находим

при i = 1 :

k₁^{[ 0 ]} =0.1( 0 + 1 ) = 0.1 ; k₂^{[ 0 ]} = 0.1( 0 + 0.05 + 1 + 0.05) = 0.11 ;

k₃^{[ 0 ]} = 0.1( 0 + 0.05 + 1 + 0.055) = 0.1105

k₄^{[ 0 ]} = 0.1( 0 + 0.1 + 1 + 0.1105) = 0.121050

x₁= 0 + 0.1 = 0.1 ; y₁ = 1 +( 1/6 )( 0.1 + 2*0.11+2*0.1105+

+0.12105 ) = 1.110342 ;

при i = 2 :

k₁^{[ 1 ]} =0.1( 0.1 + 1.110342 ) = 0.1210342 ;

k₂^{[ 1 ]} = 0.1( 0.1 + 0.05 + 1.110342 + 0.0605171) = 0.1326385 ;

k₃^{[ 1 ]} = 0.1( 0.1 + 0.05 + 1.110342 + 0.06604295) = 0.1326385 ;

k₄^{[ 1 ]} = 0.1( 0.1 + 0.1 + 1.110342 + 0.1326385) = 0.1442980 .

x₂= 0.1 + 0.1 = 0.2 ;

y₂ = y₁ +( 1/6 ) [ k₁^[1] + 2 k₂^[1] +2 k₃^[1] + k₄^[1]] = 1.242805 ;

Далее получаем при i = 3 x₃ = 0.3 ; y₃ = 1.399717 ;

i = 4x₄ = 0.4 ; y₄ = 1.583648 ;

С помощью программы проводим вычисления с половинным шагом . Результаты заносим в таблицу .

2. Блок - схемачисленного решения задачи Коши для дифференциального уравнения первого порядка методами Эйлера , Эйлера - Коши и Рунге - Кутта

Методом   Рунге -   Кутта

Методом   Эйлера -   Коши

Методом Эйлера

Вычисление приближенного решения на одном шаге

3. Пример программы для функции y ^/ = x + y

program DifEquationsFirstOrder;

{*******************************************************}

uses Crt;

const

c:array[1..4] of real = (0,0.5,0.5,1);

type

coef = array[0..4] of real;

var

i,j,m:integer;

a,b,h,x,y,y1,y2,y3:real;

k0,k:coef;

ch:char;

{-----------------------SUBROUTINES---------------------}

{ Y = F ( x ,y ) (f = x+y) }

function f(x,y:real):real;

BEGIN

f := x + y

END;

{-------------------------------------------------------}

procedure Pausa;

BEGIN

WRITELN;WRITELN ( 'Для продолжения нажмите любую клавишу ...');

REPEAT ch := readkey UNTIL ch <> '';

END;

{------------------ОСНОВНАЯ ПРОГРАММА-------------------}

BEGIN

ClrScr;

WRITELN ( 'Введите значения концов отрезка [a,b]');

READ (a,b);

WRITELN ( 'Введите начальное значение функции y0 при x=x0 ');

READ (y);

WRITELN (' Введите число значений функции на промежутке [a,b]');

READ (m);

x:= a; h:= (b-a) / m; y1:= y; y2:= y; y3:=y;

WRITELN (' Метод Эйлера Метод Э.-Коши Метод Р.-Кутта');

WRITELN ( 'x=' ,x:5:2,' y1=',y:9:6,' y2=',y2:9:6,' y3=',y3:9:6);

FOR i:= 1 TO m DO

BEGIN

y1:= y1 + h*f(x,y1);

FOR j:=1 TO 2 DO

k0[j]:=h*f(x+2*c[j]*h , y2+2*c[j]*k0[j-1]);

y2:= y2+(k0[1]+k0[2]) / 2 ;

FOR j:=1 TO 4 DO

k[j]:= h*f(x+c[j]*h, y3+ c[j]*k[j-1]);

y3:= Y3+ (k[1]+2*k[2]+2*k[3]+k[4]) / 6;

x:= x+h;

WRITELN ('x=',x:5:2,' y1=',y1:9:6,' y2=',y2:9:6,' y3=',y3:9:6);

END;

PAUSA;

END.