МКЭ для уравнений 4-го порядка
Для краевой задачи
 ; (1.32)
; (1.32)
 (1.33)
(1.33)
введем понятие обобщенного решения. Для этого рассмотрим подпространство пространства  .
.  – это множество функций из
– это множество функций из 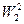 , удовлетворяющих условиям (1.33).
, удовлетворяющих условиям (1.33).
Пусть  произвольная функция. Умножим (1.32) на
произвольная функция. Умножим (1.32) на 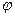 скалярно и проведем интегрирование по частям. Получим
скалярно и проведем интегрирование по частям. Получим
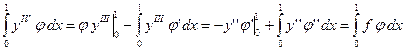 ,
,
или, короче,
 . (1.34)
. (1.34)
Решение краевой задачи (1.32), (1.33) удовлетворяет (1.34) при произвольной функции  . Верно и обратное. Функция
. Верно и обратное. Функция 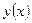 , удовлетворяющая (1.34) при любой
, удовлетворяющая (1.34) при любой  и имеющая 4 производные является решением краевой задачи (1.32), (1.33).
и имеющая 4 производные является решением краевой задачи (1.32), (1.33).
Обобщенным решением задачи (1.32), (1.33) называется функция из  , удовлетворяющая (1.34) при произвольной
, удовлетворяющая (1.34) при произвольной  .
.
Чтобы применить МКЭ, нужно задать координатные функции. Согласно (1.34) нужны функции, принадлежащие  , так что кусочно-линейные функции не подходят.
, так что кусочно-линейные функции не подходят.
Построим координатные функции следующим образом. Как и ранее, введем на промежутке 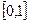 сетку узлов
сетку узлов 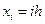 ,
, 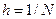 . Каждому узлу сетки
. Каждому узлу сетки 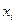 сопоставим по две координатные функции
сопоставим по две координатные функции 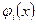 и
и  , которые на каждом из участков
, которые на каждом из участков  являются полиномами не выше третьей степени. Эти функции можно задать с помощью следующих двух стандартных функций (рис.4):
являются полиномами не выше третьей степени. Эти функции можно задать с помощью следующих двух стандартных функций (рис.4):

Рис.4. Функции, задающие координатные функции кусочно-эрмитова восполнения

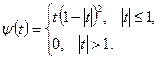
Эти функции равны нулю вне отрезка 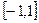 . На концах его, т.е. при
. На концах его, т.е. при 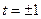 , они удовлетворяют условиям (1.33). Кроме того:
, они удовлетворяют условиям (1.33). Кроме того:
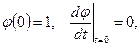

Очевидно, что 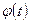 ,
,  непрерывны вместе с первыми производными при
непрерывны вместе с первыми производными при 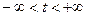 .
.
Теперь положим
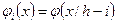 ,
, 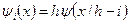 ,
, 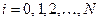 .
.
Каждая из функций 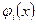 и
и  непрерывна на
непрерывна на 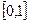 вместе с первой производной и, следовательно, принадлежит
вместе с первой производной и, следовательно, принадлежит 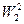 . Кроме того:
. Кроме того:
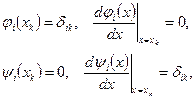
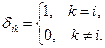
При этом на каждом из отрезков  функции
функции 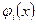 и
и  суть полиномы не выше третьей степени. Кроме того,
суть полиномы не выше третьей степени. Кроме того, 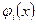 отлична от нуля на
отлична от нуля на  , так же как и
, так же как и  .
.
Пусть на отрезке 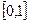 задана непрерывно дифференцируемая функция
задана непрерывно дифференцируемая функция  . Каждому узлу сетки
. Каждому узлу сетки 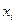 сопоставим по два параметра:
сопоставим по два параметра:
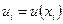 ,
, 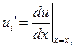 .
.
По этому набору параметров построим функцию  , являющуюся на каждом интервале
, являющуюся на каждом интервале  полиномом не выше третьей степени и удовлетворяющую условиям
полиномом не выше третьей степени и удовлетворяющую условиям
 ,
, 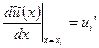 .
.
Построенная функция  является на каждом интервале
является на каждом интервале  интерполяцией по Эрмиту функции
интерполяцией по Эрмиту функции  . С помощью функций
. С помощью функций 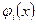 ,
,  функцию
функцию  можно представить так:
можно представить так:
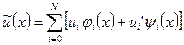 .
.
Множество функций, представимых в виде
 , (1.35)
, (1.35)
образуют конечномерное подпространство в  , базис которого составляют функции
, базис которого составляют функции 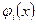 ,
,  ,
, 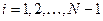 . Обозначим это подпространство через
. Обозначим это подпространство через  .
.
Приближенное решение задачи (1.32), (1.33) определим как функцию из  , удовлетворяющую уравнению
, удовлетворяющую уравнению
 ,
,
при произвольной функции  . Тогда система уравнений для определения неизвестных коэффициентов
. Тогда система уравнений для определения неизвестных коэффициентов 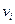 и
и 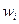 ,
, 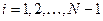 примет вид
примет вид

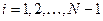 . (1.36)
. (1.36)
Предоставив читателям все необходимые вычисления (см. А. А. Самарский и В. Б. Андреев), выпишем сеточные уравнения системы (1.36) подробно:
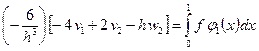 ,
,
 ,
,
 ,
, 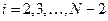 , (1.37)
, (1.37)
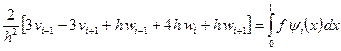 ,
, 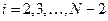 ,
,
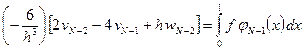 ,
,
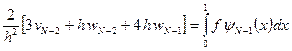 .
.
Матрица системы (1.36) симметрична и имеет не более семи ненулевых диагоналей. Это свойство является следствием ''почти'' ортогональности между собой базисных функций. Уравнения (1.37) несколько меньше напоминают классическую разностную схему, чем это было для уравнений второго порядка. Однако если из системы (1.37) исключить неизвестные 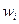 , то для определения
, то для определения 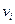 мы получим систему, аналогичную классической разностной схеме.
мы получим систему, аналогичную классической разностной схеме.
