Нижегородская (III открытая) городская математическая олимпиада школьников

Нижегородская (III открытая) городская математическая олимпиада школьников

г. Нижний Новгород, НФ ГУ ВШЭ, 18 декабря 2005 года

Класс

1. Можно ли, записав подряд несколько натуральных чисел – целочисленных степеней двойки, получить число, кратное 2005? (Е.Бурков, 5 курс, ННГУ)

2. Новая шахматная фигура «лягушка» поочерёдно делает ходы на 1, 2, 1, 2, … клетки (по горизонтали или вертикали). Может ли лягушка обойти всю доску 8´8, побывав на каждой клетке ровно 1 раз? (А.Смирнов, 1 курс, НФ ГУ ВШЭ)

3. К – середина медианы ВМ треугольника АВС. Прямая СК пересекает сторону АВ в точке Р. Докажите, что если АК=МС, то DВРК – равнобедренный. (В.Шмаров, 10 кл., лицей №15, г.Саров)

4. Чему равен Ч´Е´Л´О´В´Е´К, для которого 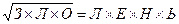? (одинаковые буквы – одинаковые цифры, разные буквы – разные цифры) (Д.Костерин, 11 кл., лицей №82, г.Н.Новгород &K)(Д.Костерин&K)

Ответ: 0. Решение: Если ни одна из букв не равна 0, то 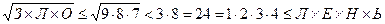,т.е. уравнение не имеет решений. Значит, уравнение имеет решение только тогда, когда обе части равны нулю, а это возможно только при Л=0, следовательно, Ч´Е´Л´О´В´Е´К=0.

5. Даны 2005 отрезков длиной 1, 2, 3, …, 2005. Два игрока по очереди берут себе по одному отрезку, пока не останется ровно 3 отрезка. Если из этих трёх оставшихся отрезков можно сложить треугольник, то выигрывает первый игрок, если нельзя – то второй. Кто выигрывает при правильной игре, первый или второй игрок? (В.А.Рузанов, лицей №40, г.Н.Новгород)

Нижегородская (III открытая) городская математическая олимпиада школьников

г. Нижний Новгород, НФ ГУ ВШЭ, 18 декабря 2005 года

9 класс

1. Разрежьте на 4 части по клеточкам фигуру, изображённую на рисунке, и сложите из них квадрат. (В.Шмаров, 10 кл., лицей №15, г.Саров)

2. Новая шахматная фигура «лягушка» поочерёдно делает ходы на 1, 2, 3, 1, 2, 3,… клетки (по горизонтали или вертикали). Может ли лягушка обойти всю доску 8´8, побывав на каждой клетке ровно 1 раз? (А.Смирнов, 1 курс, НФ ГУ ВШЭ &K)

3. Внутри DABC проведены отрезки AD, CE (D, E принадлежат BC и AB соответственно). Пусть O – точка пересечения AD и CE. Оказалось, что ÐDAC=ÐECB, ÐBAD=ÐOBC. Докажите, что D – середина стороны ВС. (К.Голубев, 11 кл., лицей №165, г.Н.Новгород)

4. Какое наибольшее количество чисел может быть в последовательности, в которой все числа являются квадратами натуральных чисел и каждое следующее число получается из предыдущего приписыванием к нему справа одной цифры? (Е.Бурков, 5 курс, ННГУ)

5. По кругу по часовой стрелке стоят числа 1, 2, 3, …, 2006 (в указанном порядке). Если по кругу стоят подряд 4 числа a, b, c, d в указанном порядке, то разрешается одновременно заменить b на (a+c-d) и c на (b+d-a). Можно ли с помощью таких операций добиться того, чтобы с некоторого места числа стояли по кругу в следующем порядке 3, 2, 1, 4, 5, …, 2006? (В.Шмаров, 10 кл., лицей №15, г.Саров)