Оптимизационные модели
Оптимизационная модель представляет собой модель математического программирования, состоящую из целевой функции и системы ограничений в форме уравнений или неравенств, и направлена на поиск наиболее эффективного (оптимального) управленческого решения при соблюдении установленных ограничений.
Целевая функция описывает цель оптимизации и представляет собой зависимость показателя, по которому ведётся оптимизация, от искомых переменных. На макроуровне критерием оптимальности может являться максимум валового национального дохода, максимум среднедушевого денежного дохода. На микроуровне: максимум прибыли предприятия, минимум затрат и др.
Например, общий вид модели для расчета оптимального варианта производства продукции на предприятии:
Целевая функция: 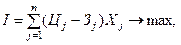
Система ограничений:
ограничения по сбыту 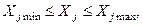
ограничения по мощности 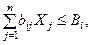
ограничения по снабжению 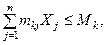
условие неотрицательности 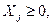
где 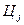 - цена реализации единицы товара
- цена реализации единицы товара 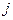 -го вида;
-го вида;
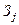 - затраты на изготовление единицы товара
- затраты на изготовление единицы товара 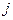 -го вида;
-го вида;
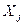 - количество товара
- количество товара 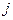 -го вида, подлежащее изготовлению;
-го вида, подлежащее изготовлению;
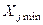 - обязательный минимальный объем производства товара
- обязательный минимальный объем производства товара 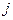 -го вида, обусловленный необходимостью выполнения уже заключённых договоров или необходимостью сохранения своего присутствия с минимальным предложением на рынках, привлекательных в долгосрочном периоде;
-го вида, обусловленный необходимостью выполнения уже заключённых договоров или необходимостью сохранения своего присутствия с минимальным предложением на рынках, привлекательных в долгосрочном периоде;
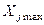 - максимально возможный объём реализации товара
- максимально возможный объём реализации товара 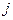 -го вида;
-го вида;
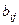 - норма затрат времени по изготовлению единицы товара
- норма затрат времени по изготовлению единицы товара 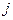 -го вида на оборудовании
-го вида на оборудовании  -го вида;
-го вида;
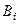 - фонд рабочего времени на оборудовании
- фонд рабочего времени на оборудовании  -го вида;
-го вида;
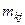 - нора затрат материала
- нора затрат материала 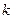 -го вида на изготовление единицы товара
-го вида на изготовление единицы товара 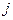 -го вида;
-го вида;
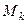 - имеющийся фонд
- имеющийся фонд 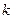 -го вида сырья.
-го вида сырья.
Оптимизационные модели могут носить детерминированный и стохастический характер. В детерминированных моделях результат решения однозначно зависит от входных параметров. Стохастические (вероятностные) модели в отличие от детерминированных описывают случайные процессы, в которых результат всегда остаётся неопределённым. В настоящее время разработано большое количество программных пакетов, позволяющих решать сложные оптимизационные задачи на основе ЭВМ.
Пример Малое предприятие изготавливает и реализует два вида продукции. Количество ресурсов, имеющихся на складе предприятия и нормы их затрат на изготовление продукции представлены в таблице 13:
Таблица 13
Ресурсы предприятия и нормы их затрат
| Ресурс | Норма затрат ресурсов, кг | Количество ресурсов, кг | |
| Продукция 1-го вида | Продукция 2-го вида | ||
Прибыль от реализации продукции 1-го вида – 2 руб/шт., 2-го вида – 3 руб/шт. Сколько продукции каждого вида следует изготовить, чтобы получить максимально возможную прибыль.
Решение:
Обозначим искомое количество продукции первого вида 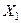 , а второго вида
, а второго вида 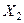 , тогда целевая функция, максимизирующая прибыль предприятия будет иметь вид:
, тогда целевая функция, максимизирующая прибыль предприятия будет иметь вид:
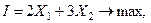
Система ограничений:
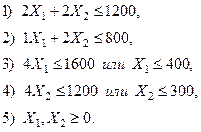
Наиболее простой и быстрый путь решения данной задачи – использование средств ЭВМ. Более трудоёмкий способ решения – графический.
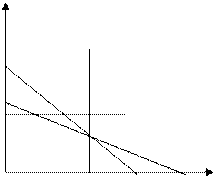
По осям отложим количество продукции 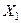 и
и 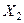 . Построим линии ограничения (на графике они пронумерованы соответственно номерам неравенств в модели). Область возможных значений объёмов производства продукции заштрихована пунктирными линиями. Оптимальному варианту производства продукции соответствуют либо координаты точки А или координаты точки К (рис.7).
. Построим линии ограничения (на графике они пронумерованы соответственно номерам неравенств в модели). Область возможных значений объёмов производства продукции заштрихована пунктирными линиями. Оптимальному варианту производства продукции соответствуют либо координаты точки А или координаты точки К (рис.7).
 |
600 1
400 К




 300
300 


 А
А
400 600 800 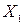
Рис.7. Графическое решение оптимизационной задачи.
Найдем координаты точек А и К.
Для точки А: 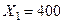 , подставляя в неравенство 1 или 2 имеем
, подставляя в неравенство 1 или 2 имеем 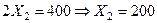 .
.
Прибыль 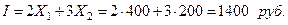
Для точки К 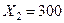 , подставляя в неравенство 2 имеем
, подставляя в неравенство 2 имеем 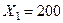 .
.
Прибыль 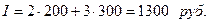
Наибольшая прибыль соответствует точке А.
Ответ: Необходимо изготовить 400 единиц продукции первого вида и 200 второго.
Особенностью оптимизационных моделей с которой приходится считаться при их использовании является однокритериальность. То есть поиск лучшего решения осуществляется по одному критерию. В то же время большинство социально-экономических процессов характеризуется системой показателей. Поэтому при математическом описании сложных, протекающих во времени экономических процессов, характеризуемых несколькими показателями часто используются имитационные модели.
Имитационные модели
Имитационными называются модели, воспроизводящие реальные соотношения между экономическими показателями, описывающими прогнозируемый объект.
В настоящее время имитационные модели разрабатываются как программы для ЭВМ, позволяющие с помощь средств вычислительной техники «проигрывать» (проводить много вариантные расчёты) развития сложных систем. Имитационная модель учитывает временной фактор и наряду с математическими моделями, имитирующими прогнозируемый процесс, содержит блоки, в которых решения принимаются человеком (прогнозистом). Имитация процессов организуется в форме диалога и у прогнозиста имеется возможность на каждом этапе принятия решения, анализируя и оценивая последствия принятия того или иного решения выбрать самое рациональное, по его мнению, решение.
В последние годы имитационные модели находят все более широкое применение для имитации экономических процессов, в которых сталкиваются различные интересы, типа конкуренции на рынке.
Имитационные модели, как и структурные модели, требуют больших трудозатрат на их разработку и высокой квалификации специалистов.
Модели теории игр
Модели теории игр направлены на математическое описание и выбор решений в конфликтных ситуациях, при которых интересы участников либо противоположны (антагонистические игры), либо не совпадают, хота и не противоположны (игры с противоположными интересами). Для конфликтных ситуаций характерно то, что ни одна из сторон не может полностью контролировать ситуацию и эффективность решений, принимаемых в ходе конфликта каждой из сторон, зависит от действий другой стороны.
Теория игр впервые была систематически изложена О.Моргенштерном и Дж. фон Нейманом в 1944 году и содержала в основном экономические примеры, поскольку экономическому конфликту легче всего придать численную форму. Во время второй мировой войны и сразу после неё теорией игр серьёзно заинтересовались военные, которые увидели в ней аппарат для исследования стратегических решений. В СССР аппарат теории игр для разрешения экономических конфликтов практически не использовался, так как, директивная система планирования исключала наличие конфликтных ситуаций в экономике. С переходом к рыночным отношениям применение моделей теории игр для оценки конфликтных ситуаций и принятия решений в условиях неопределённости стало актуальным.
Содержание игры заключается в том, что каждый из её участников выбирает такую стратегию действий, которая, как он полагает, обеспечивает ему максимальный выигрыш (минимальный проигрыш). Стратегию игрока называют оптимальной, если при её применении выигрыш данного игрока не уменьшается, какими бы стратегиями не пользовался его противник. Результаты принимаемых решений заносятся в специальную таблицу, которая называется матрицей игры или платёжной матрицей. При поиске оптимальных стратегий в теории игр игроки опираются на принцип максимальной осторожности. Данный принцип гласит, что каждый игрок, считая партнёра по игре высоко интеллектуальным соперником, выбирает свою стратегию в предположении о том, что соперник не упустит ни единой возможности использовать его ошибку в своих интересах.
В экономической практике часто приходится придавать игровую форму таким ситуациям, в которых один из участников безразличен к результату игры. Такие игры называют статистическими или играми с «природой», понимая под «природой» всю совокупность внешних обстоятельств. В играх с «природой» степень неопределённости для сознательного игрока возрастает, так как «природа», будучи индеферентной в отношении выигрыша, может предпринимать и такие ответные действия, которые ей совершенно не выгодны.
Рассмотрим игровую ситуацию, в которой игроки 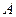 и
и 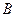 должны принять с каждой стороны по одному решению из трёх возможных. Результаты принимаемых решений (выигрыши игрока
должны принять с каждой стороны по одному решению из трёх возможных. Результаты принимаемых решений (выигрыши игрока 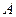 ) занесены в платёжную матрицу (табл.14)
) занесены в платёжную матрицу (табл.14)
Действия игрока 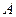 :
:
1. Определяется для каждого решения минимальное значение 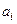 , ожидаемого выигрыша
, ожидаемого выигрыша 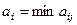 . Для нашего случая
. Для нашего случая 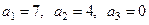 .
.
2. Из всех возможных выигрышей 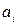 игрок
игрок 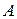 выбирает максимальное значение
выбирает максимальное значение 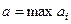 , т.е.
, т.е. 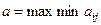 . Это
. Это 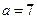 .
.
Число 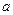 называется нижней чистой ценой игры.
называется нижней чистой ценой игры.
Действия игрока 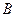 :
:
1. Определяется для каждого решения максимально возможный проигрыш 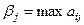 . Для нашего случая
. Для нашего случая 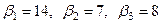 .
.
2. Из всех проигрышей игрок  выбирает минимальное значение
выбирает минимальное значение 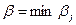 , т.е.
, т.е. 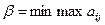 . Это
. Это 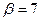 .
.
Число 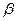 называется верхней чистой ценой игры.
называется верхней чистой ценой игры.
Таблица 14
Платёжная матрица
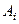 | 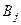 | 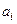 | ||
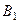 | 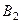 | 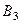 | ||
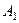 | 7 | |||
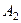 | ||||
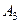 | ||||
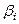 |
Таким образом, в нашей игровой ситуации имеется «седловая» точка 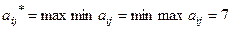 - наименьшая в строке и наибольшая в столбце, и соответственно, игроку
- наименьшая в строке и наибольшая в столбце, и соответственно, игроку 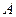 следует принять 1 решение, а игроку
следует принять 1 решение, а игроку 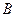 - 2.
- 2.
Однако на практике достаточно часто возникают игровые ситуации, не имеющие чётко выраженных «седловых» точек. Платёжная матрица такой ситуации представлена в таблице 15.
Таблица 15
Платёжная матрица
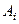 | 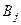 | 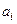 | |
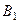 | 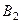 | ||
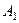 | |||
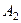 | |||
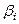 |
В этом случае игрокам необходимо использовать смешанные стратегии. Обозначим через 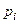 вероятности, с которыми игрок
вероятности, с которыми игрок 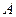 принимает свои решения (
принимает свои решения ( 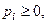
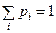 ). Обозначим через
). Обозначим через 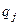 вероятности, с которыми игрок
вероятности, с которыми игрок 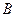 принимает свои решения (
принимает свои решения ( 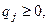
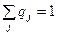 ). Тогда величина выигрыша будет являться функцией от вероятностей принимаемых решений:
). Тогда величина выигрыша будет являться функцией от вероятностей принимаемых решений:
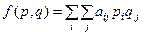 .
.
Для нашего случая:
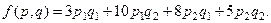
Обозначим оптимальные смешанные стратегии:
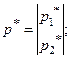
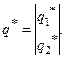
По аналогии с предыдущей ситуацией для «седловой» точки (наименьшая в строке и наибольшая в столбце) должно выполняться неравенство:
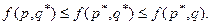
«Седловую» точку при оптимальных смешанных стратегиях называют ценой игры: 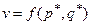 , т.е.:
, т.е.:
 .
.
Проведём преобразования:
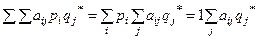 ;
;
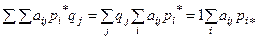 ;
;
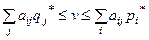 .
.
Разделим обе части неравенства на цену игры 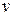 :
:
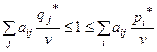 .
.
Введём обозначения:  ,
, 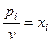 .
.
Тогда неравенство будет иметь следующий вид:
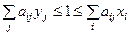 .
.
Таким образом, наша игровая ситуация сводится к решению оптимизационной задачи. Игрок 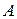 , стремясь увеличить свой выигрыш, должен минимизировать величину обратную своему выигрышу:
, стремясь увеличить свой выигрыш, должен минимизировать величину обратную своему выигрышу:
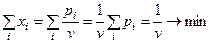 .
.
При выполнении ограничений:
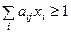 .
.
Игрок 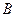 , наоборот, стремится сделать свой проигрыш меньше, а значит величину
, наоборот, стремится сделать свой проигрыш меньше, а значит величину 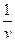 больше. Для игрока
больше. Для игрока 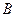 задача запишется в следующем виде:
задача запишется в следующем виде:
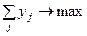 ,
,
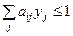 .
.
Для игрока  в рассматриваемой игровой ситуации:
в рассматриваемой игровой ситуации:

Решая данную задачу, получаем 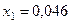 ,
, 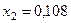 .
.
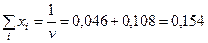 .
. 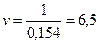 .
.
Оптимальная смешанная стратегия:
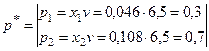 .
.
Пример Фермерское хозяйство выращивает картофель и пшеницу на площади 100 Га. Прибыль, получаемая от реализации 1 тонны картофеля –500 руб., от 1 т. пшеницы – 3000 руб. Урожайность культур зависит от погодных условий. В засушливое лето урожайность картофеля – 15 т/га, пшеницы – 3 т/га. В дождливое лето урожайность картофеля – 24 т/га, пшеницы – 2 т/га. Определить какую площадь фермерскому хозяйству необходимо отвести под картофель и пшеницу.
Решение:
1. Если на площади 100 Га посадить только картофель, то ожидаемая прибыль составляет:
- в засушливое лето 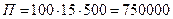 руб.,
руб.,
- в дождливое лето 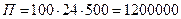 руб.
руб.
2. Если на площади 100 Га посадить только пшеницу, то ожидаемая прибыль составляет:
- в засушливое лето 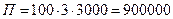 руб.,
руб.,
- в дождливое лето 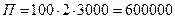 руб.
руб.
Заполним платёжную матрицу (табл.16).
Если был посажен картофель, и сложилось дождливое лето, наш проигрыш будет равен 0 (мы приняли наилучший вариант решения для сложившихся погодных условий).
Если был посажен картофель, и сложилось засушливое лето, наш проигрыш составит 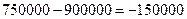 руб. (был принят не лучший вариант решения, при посадке пшеницы в засушливое лето мы получили бы 900000руб. прибыли, а так только – 750000руб.).
руб. (был принят не лучший вариант решения, при посадке пшеницы в засушливое лето мы получили бы 900000руб. прибыли, а так только – 750000руб.).
Если была посажена пшеница, и сложилось дождливое лето, наш проигрыш составит  руб. (при посадке картофеля мы получили бы 1200000 руб.).
руб. (при посадке картофеля мы получили бы 1200000 руб.).
Если была посажена пшеница, и сложилось дождливое лето, наш проигрыш будет равен 0.
Таблица 16
Платёжная матрица
| Вариант решения | Погодные условия | |
| Дождливое лето | Засушливое лето | |
| Картофель | -150000 | |
| Пшеница | -600000 |
Произведём преобразование матрицы - для того чтобы избавиться от отрицательных чисел прибавим к каждому её элементу 600000:
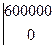
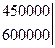 , и разделим на 150000
, и разделим на 150000
 .
.
Целевая функция:  ,
,
Ограничения: 1)  ,
,
2)  .
.
Из первого ограничения имеем: 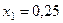 , подставим значение
, подставим значение 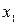 во второе ограничение:
во второе ограничение:
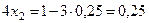
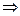
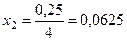 .
.
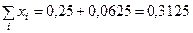 ,
, 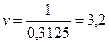 .
.
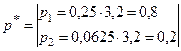
Таким образом, картофелем следует засадить 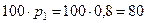 Га, а пшеницей
Га, а пшеницей 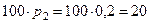 Га.
Га.
Теория игр нашла широкое применение для теоретического описания таких процессов как конкуренция на рынке. Однако, практика показывает, что основной принцип, которым оперирует теория игр (принцип максимальной осторожности, т.е. мы при выборе или поиске своего решения исходим из того, что наш конкурент является высокоинтеллектуальным человеком, принимающим лучшие решения) реализуется, по оценкам экспертов, на 20%. В основном, наши конкуренты принимают далеко не самые эффективные решения.
