Решая линейную систему (2.3) с помощью замены

План лекции

1. Общий вид однофакторной регрессионной модели

2. Метод наименьших квадратов

3. Оценка качества уравнения регрессии

4. Нелинейные регрессионные модели

5. Содержательная интерпретация параметров регрессии

1. Простейшие регрессионные модели отражают взаимосвязь показателя только с одним фактором. В общем случае однофакторную регрессионную модель можно представить в виде

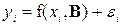, (1.1)

где

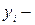значение 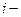ого наблюдения моделируемого показателя;

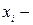значение фактора в 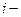ом наблюдении;

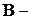вектор неизвестных параметров, которые оцениваются по статистическим данным;

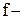функция определяющая структуру регрессионной модели (линейную, степенную и т.п.);

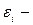ненаблюдаемая случайная величина, представляющая собой ту часть вариации показателя 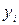, которая не объясняется соответствующими изменениями фактора .

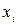Чем ниже уровень возможных значений случайной величины 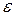, тем точнее модель отражает взаимодействие фактора х с показателем y. Т.е. параметры модели должны подбираться таким образом, чтобы минимизировать сумму квадратов отклонений (случайных составляющих )

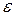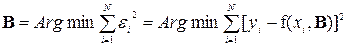. (1.2)

В общем случае поиск оптимальных параметров сводится к решению нелинейной экстремальной задачи. Обычно рассматривают линейный случай

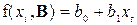, (1.3)

который значительно упрощает решение этой задачи.

2. Рассмотрим применение метода наименьших квадратов к случаю построения линейной регрессии (1.3). Для этого случая (1.2) перепишется в виде

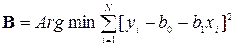. (2.1)

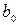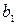Применяя дифференциальное исчисление для минимизации (2.1) и дифференцируя по и , получаем систему линейных уравнений

,

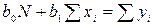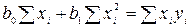. (2.2)

Разделив левую и правую части этой системы на число наблюдений N и произведя замену:

; ; ; ,

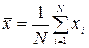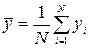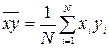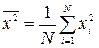перепишем систему (2.2) в виде:

,

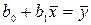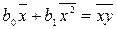. (2.3)

Решая линейную систему (2.3) с помощью замены

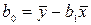
получаем оценки коэффициентов однофакторной регрессионной модели в виде:

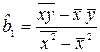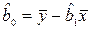; . (2.4)

Рассчитанные таким образом коэффициенты регрессии 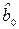, 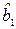принято называть оценками МНК (метода наименьших квадратов).

3. Прежде, чем построенное уравнение регрессии использовать в аналитических целях, оценивается его качество с помощью системы показателей: коэффициента корреляции, дисперсионного отношения Фишера, критерия Стьюдента.

Коэффициент корреляции показывает тесноту линейной связи между моделируемым показателем и фактором и рассчитывается по формуле

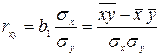, (3.1)

где

; .

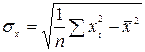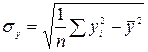Значение коэффициента корреляции заключены между -1 и 1. При 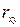=1 между показателем и фактором существует функциональная зависимость, при 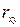=0 между показателем и фактором нет линейной связи, при 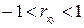имеет место корреляционная связь.

Квадрат коэффициента корреляции, умноженный на 100 ( 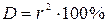), называют коэффициентом детерминации. Он показывает, насколько процентов вариация зависимой переменной y объясняется соответствующими изменениями независимой переменной x.

С помощью F-критерия (дисперсионного отношения Фишера) устанавливается адекватность регрессионной модели. Его расчет осуществляется по формуле

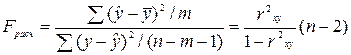, (3.2)

где

n – число элементов выборочной совокупности;

m – число факторов.

В числители критерия (3.2) стоит сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»), деленная на число степеней свободы m, а в знаменателе – остаточная сумма квадратов отклонений, деленная на (n-m-1) (остаточная дисперсия).

Если 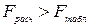, то построенная модель считается адекватной. 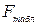- это максимально возможное значение дисперсионного отношения Фишера при данных степенях свободы и уровне значимости 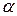. Обычно 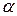принимается равным 0,05 или 0,01 и представляет собой вероятность отвергнуть правильную гипотезу при условии того, что она верна. Фактически, с помощью F-критерия проверяется 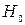- гипотеза о том, что 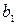=0.

Статистическая значимость каждого коэффициента регрессии в отдельности устанавливается с помощью t-критерия Стьюдента, рассчитываемого по формулам

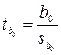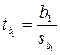; . (3.3)

Стандартные ошибки параметров линейной регрессии определяются по формулам

;

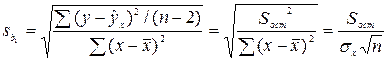(3.4)

.

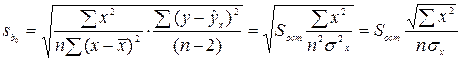Кроме критерия Стьюдента, стандартные ошибки используются при расчете предельных ошибок

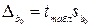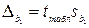; , (3.5)

которые, в свою очередь, применяются для определения доверительных интервалов.

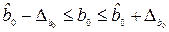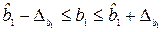; . (3.6)

Если границы доверительного интервала содержат 0, т.е. нижняя граница отрицательна, а верхняя – положительна, то оцениваемый параметр считается незначимым.

4. В случае, когда линейная модель неадекватна, строятся нелинейные регрессионные модели. Нелинейные модели принято делить на два класса: регрессии нелинейные относительно объясняющей переменной, но линейные по оцениваемым параметрам и регрессии, нелинейные по оцениваемым параметрам.

Нелинейные по объясняющей переменной:

· парабола ;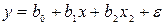

· полином третьей степени ;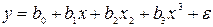

· равносторонняя гипербола .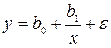

Нелинейные по оцениваемым параметрам:

· показательная ;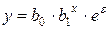

· степенная ;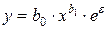

· экспоненциальная .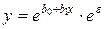

Коэффициенты моделей первого класса рассчитываются с помощью метода наименьших квадратов. Построение моделей второго класса требует предварительного их приведения к линейному виду путем логарифмирования.

;

;

.

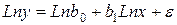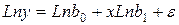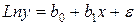После построения с помощью метода наименьших квадратов преобразованных моделей коэффициенты исходных моделей в случае необходимости получаются путем потенцирования.

Теснота связи между фактором и показателем в нелинейных моделях измеряется с помощью индекса корреляции

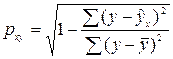, (4.1)

границы изменения которого 0 и 1. Чем ближе значение индекса корреляции к 1, тем теснее связь.

Адекватность нелинейных моделей, как и в линейном случае, определяется с помощью дисперсионного отношения Фишера (F-критерия).

5. Если построенная модель адекватна, то становится правомерным ее практическое использование в аналитических целях. Практическое использование требует содержательной интерпретации результатов эконометрического моделирования.

Коэффициент линейной модели 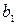является коэффициентом абсолютного роста. Он показывает на сколько единиц изменится показатель y, если фактор x изменится на 1.

В показательной модели 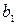является коэффициентом относительного роста. Он показывает во сколько раз изменится y, если x изменится на 1.

В степенной модели 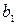является коэффициентом эластичности. Он показывает на сколько % изменится y, x изменится на 1 %.