Формула полной вероятности
Зависимые события, условные вероятности, вывод формулы, признак независимости событий, формула полной вероятности,формулаБайеса,ее практическое приминение.
Условная вероятность есть вероятность осуществления одного из событий при условии, что другое событие состоялось. Обозначение условных вероятностей:
P(B/A)- условная вероятность события B при условии осуществления события A,
P(A/B) - условная вероятность события A при условии осуществления события B.
Найдем условную вероятность, например, P(B/A)с помощью классического определения вероятности по п. 1.2.2. Для этого необходимо знать общее количество n предполагаемых испытаний, в результате которых могут осуществиться события A, B, A 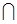 B.
B.
Общее количество исходов, при которых возможна реализация условного событияB/A, определяется исключительно числом появления события A, поскольку, если оно не осуществится, то не осуществится и условное событиеB/A.Пусть m - число исходов, благоприятствующих появлению события A. Понятно, что в общем случае 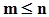 .
.
В результате предполагаемых испытаний событие B может появиться и без появления события A, но условное событие B/A осуществляется только при совместном появлении событий A и B. В связи с этим число случаев, благоприятствующих появлению событияA 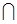 B,равно количеству случаев, благоприятствующих появлению события B/Aили события A/B.Обозначим это количество через s.
B,равно количеству случаев, благоприятствующих появлению события B/Aили события A/B.Обозначим это количество через s.
Тогда в соответствии с классическим определением вероятности
P(В/А)= 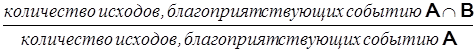 , то есть
, то есть
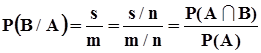 .
.
Таким образом, условная вероятность P(В/А) определяется, как 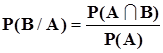 .Точно так же
.Точно так же 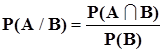 .
.
Из полученных выражений следует, что 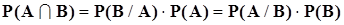 .
.
События A и B независимы, когда P(B/A)=P(B) и P(A/B)=P(A).
Отсюда следует формулировка признака независимости случайных событий: событияA и Bнезависимы тогда и только тогда, когдаP(A 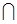 B)=P(A)×P(B).В самом деле, при таком соотношении
B)=P(A)×P(B).В самом деле, при таком соотношении  Если A и Bсвязаны взаимно однозначно, тоm=s, а потому
Если A и Bсвязаны взаимно однозначно, тоm=s, а потому
P(A  B)=P(A)=P(B), P(B/A)=1, P(A/B)=1.
B)=P(A)=P(B), P(B/A)=1, P(A/B)=1.
Формула полной вероятности
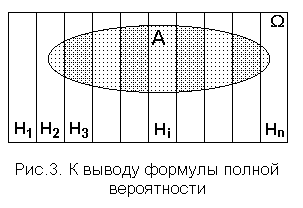 |
Пусть при условиях S в W возможно событие A. Кроме того вWопределена полная группа попарно непересекающихся событий 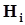 , i=1,2,...,n, то есть
, i=1,2,...,n, то есть 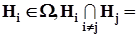 Æ,
Æ, 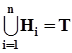 .Данная ситуация представлена на рис. 3. Из предъявленных соотношений и из рисунка 3 следует, что
.Данная ситуация представлена на рис. 3. Из предъявленных соотношений и из рисунка 3 следует, что 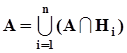 .Воспользовавшись аксиомой Колмогорова о счетной аддитивности вероятностной меры и математическим определением условных вероятностей, получим:
.Воспользовавшись аксиомой Колмогорова о счетной аддитивности вероятностной меры и математическим определением условных вероятностей, получим: 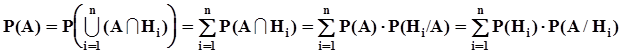 . Таким образом получена формула полной вероятности:
. Таким образом получена формула полной вероятности: 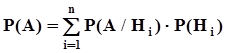 ,в которой события
,в которой события 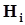 именуются гипотезами.
именуются гипотезами.
Формула БайесаВоспользовавшись формулой для условной вероятности и формулой полной вероятности, получим ценную для многочисленных приложений формулу Байеса:
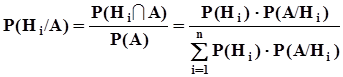 .Формула Байеса эффективно используется при исследованиях природных явлений, при исследованиях и испытаниях рукотворных объектов в условиях неопределенности математической модели исследуемых объектов и действия мешающих случайных воздействий. В этих условиях события, происходящие при исследованиях, неоднозначно связаны со свойствами и параметрами объектов.
.Формула Байеса эффективно используется при исследованиях природных явлений, при исследованиях и испытаниях рукотворных объектов в условиях неопределенности математической модели исследуемых объектов и действия мешающих случайных воздействий. В этих условиях события, происходящие при исследованиях, неоднозначно связаны со свойствами и параметрами объектов.
Пусть 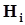 - гипотезы или предположения исследователя о свойствах или параметрах исследуемого объекта, рукотворного или природного. Эти гипотезы могут иметь одинаковый или различный приоритет, который выражается путем задания значений вероятностей
- гипотезы или предположения исследователя о свойствах или параметрах исследуемого объекта, рукотворного или природного. Эти гипотезы могут иметь одинаковый или различный приоритет, который выражается путем задания значений вероятностей 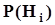 . Эти вероятности в данной ситуации суть априорные вероятности гипотез
. Эти вероятности в данной ситуации суть априорные вероятности гипотез 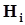 .
.
В результате эксперимента или исследования событиеA происходит с той или иной вероятностью. Это событие исследователь фиксирует и по немуон должен вынести суждение об оправданности того или иного априорного предположения (гипотезы). В силу действия случайных факторов и неопределенности математической модели объекта однозначные причинно-следственные связи между предположениями (гипотезами) исследователя и результатами испытаний размыты. После выполнения эксперимента (испытания) фиксируется событие A. В этой ситуации можно оценить условные вероятности 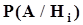 возможности реализации события A при справедливости каждой из гипотез. Таким образом после эксперимента правая часть формулы Байеса может быть рассчитана, и формула Байеса дает возможность оценить апостериорную вероятность той или иной гипотезы при условии, что результатом эксперимента оказалось событие A.
возможности реализации события A при справедливости каждой из гипотез. Таким образом после эксперимента правая часть формулы Байеса может быть рассчитана, и формула Байеса дает возможность оценить апостериорную вероятность той или иной гипотезы при условии, что результатом эксперимента оказалось событие A.
Естественно принять в качестве наиболее правдоподобного то предположение (гипотезу), апостериорная вероятность которого окажется наибольшей. Такое правило принятия решения, которое основано на применении формулы Байеса, называется байесовским. Этой же формулой порожден принцип максимума апостериорной вероятности, который часто и эффективно используется в теории и практике систем автоматического регулирования, при математической обработке результатов измерений, при идентификации объектов.
Наиболее широкое применение байесовский принцип максимума апостериорной информации находит в системах передачи информации по каналам связи, в которых велика вероятность искажения передаваемых символов и сообщений. Обычно это цифровые каналы. В них на передающей стороне применяется избыточное кодирование сообщений, а на приемной стороне устанавливается байесовский декодер, реализующий указанный байесовский принцип в реальном времени.
3.Последовательность независимых событий,биномиальноераспределение,наивероятное число событий,определение мат ожидания и дисперсии через производящую функцию моментов,теоремы Пуассона и Муавра-Лапласа.
При постоянных условиях S выполняется n независимых испытаний. Результатом каждого испытания может быть только одно из двух противоположных событий:A или 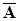 . Введем обозначения для вероятностей этих событий: P(A) = p, P(
. Введем обозначения для вероятностей этих событий: P(A) = p, P( 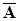 ) = q = 1 - p.
) = q = 1 - p.
Требуется найти вероятность 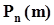 того, что при указанных условиях событие A произойдет ровно m раз. Количество комбинаций, в которых событие A произойдет ровно m раз, может быть несколько. Реализация каждой такой комбинации есть сложное событие, которое представляет собой последовательность событий A и
того, что при указанных условиях событие A произойдет ровно m раз. Количество комбинаций, в которых событие A произойдет ровно m раз, может быть несколько. Реализация каждой такой комбинации есть сложное событие, которое представляет собой последовательность событий A и 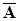 .
.
Обозначим эти сложные события буквой B, индекс у которой будет соответствовать номеру одной из возможных последовательностей:
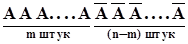 =
= 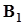 . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . 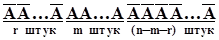 =
= 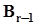 . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . 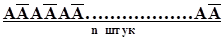 =
= 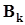 .
.
Общее количество таких последовательностей равно числу сочетаний из n по m, поскольку порядок следования их элементов неразличим, то есть 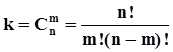 .События
.События 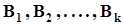 попарно несовместны, поэтому в соответствии с аксиомой о счетной аддитивности
попарно несовместны, поэтому в соответствии с аксиомой о счетной аддитивности 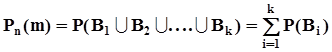 , но
, но 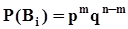 независимо от i , поэтому вероятность того, что при n независимых испытаниях событие A появится ровно m раз, равна
независимо от i , поэтому вероятность того, что при n независимых испытаниях событие A появится ровно m раз, равна 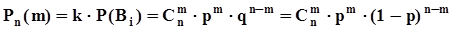 .Биномиальное распределение вероятностей
.Биномиальное распределение вероятностей
Схема Бернулли порождает дискретную случайную величину, а именно, количество случаев появления события A в последовательности n независимых испытаний. Множество значений, которые может принимать эта случайная величина :m = 0, 1, 2, 3, ..., n. Вероятности, с которыми случайная величина принимает эти значения: 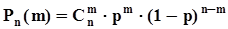 . Для того, чтобы убедиться, является ли набор этих вероятностей распределением, просуммируем их с использованием формулы бинома Ньютона:
. Для того, чтобы убедиться, является ли набор этих вероятностей распределением, просуммируем их с использованием формулы бинома Ньютона: 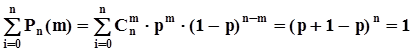 .Таким образом, случайная величина, порожденная испытаниями по схеме Бернулли, задана своими значениями и распределением вероятностей:
.Таким образом, случайная величина, порожденная испытаниями по схеме Бернулли, задана своими значениями и распределением вероятностей:
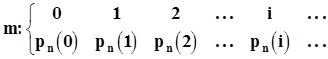 Это распределение называется биномиальным распределением.Для того, чтобы представить вид этого распределения, исследуем его на максимальное значение. Для этого вычислим отношение двух соседствующих значений вероятностей:
Это распределение называется биномиальным распределением.Для того, чтобы представить вид этого распределения, исследуем его на максимальное значение. Для этого вычислим отношение двух соседствующих значений вероятностей:
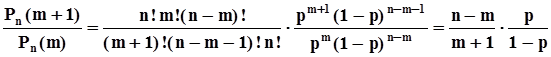 .
.
Выясним интервал возрастания вероятности, то есть интервал, в котором 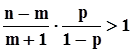 .В этом неравенстве все сомножители, делимые и делители больше нуля, поэтому его самостоятельное решение не вызовет затруднений. В результате получим, что интервал монотонного возрастания вероятности простирается от m = 0 до m = Ent[np+p-1], где Ent[ · ] - целая часть числа.Точно так же отыскивается область монотонного убывания:
.В этом неравенстве все сомножители, делимые и делители больше нуля, поэтому его самостоятельное решение не вызовет затруднений. В результате получим, что интервал монотонного возрастания вероятности простирается от m = 0 до m = Ent[np+p-1], где Ent[ · ] - целая часть числа.Точно так же отыскивается область монотонного убывания: 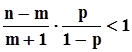 ,откуда получаем, что монотонное убывание вероятности начинается от значения m = Ent[np+p]. Итак, мы нашли, что наибольшее значение вероятность
,откуда получаем, что монотонное убывание вероятности начинается от значения m = Ent[np+p]. Итак, мы нашли, что наибольшее значение вероятность 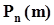 в схеме Бернулли принимает при значении m, ближайшем к np. А это, в свою очередь, означает, что ближайшее целое к np есть наиболее вероятное значение числа появления события A в схеме Бернулли
в схеме Бернулли принимает при значении m, ближайшем к np. А это, в свою очередь, означает, что ближайшее целое к np есть наиболее вероятное значение числа появления события A в схеме Бернулли
Производящей функцией моментов случайной величины x называется математическое ожидание функции y(n) = exp(nx), где n - аргумент производящей функции моментов: 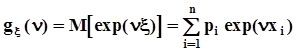 .Пример.Написать производящую функцию моментов для биномиального распределения и вычислить математическое ожидание и дисперсию случайной величины, распределенной по биномиальному закону.
.Пример.Написать производящую функцию моментов для биномиального распределения и вычислить математическое ожидание и дисперсию случайной величины, распределенной по биномиальному закону.
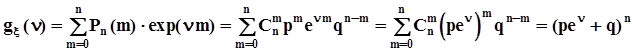 .
.
Первая производная от 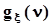 по n
по n 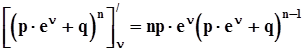 .Вторая производная от
.Вторая производная от 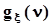 по n
по n 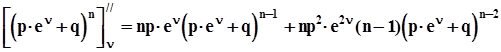 .Вычислим эти производные при n = 0:
.Вычислим эти производные при n = 0: 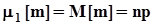 ,
, 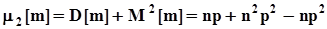 .Окончательно получим: M[m]=np, D[m]=np(1-p) = npq.Сопоставляя полученное выражение для математического ожидания числа появления события A в испытаниях по схеме Бернулли с наиболее вероятным значением этого числа, видим, что они совпадают..
.Окончательно получим: M[m]=np, D[m]=np(1-p) = npq.Сопоставляя полученное выражение для математического ожидания числа появления события A в испытаниях по схеме Бернулли с наиболее вероятным значением этого числа, видим, что они совпадают..
Теорема ПуассонаАнализируется ассимптотическое поведение вероятности появления m событий в схеме Бернулли при n ®¥, np = const = a. Цель - упрощение вычислений, трудоемкость которых сильно возрастает с ростом n.
Задача состоит в нахождении предела последовательности:

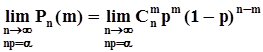 .Из равенства np = a следует, что p=
.Из равенства np = a следует, что p= 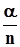 . Кроме того
. Кроме того 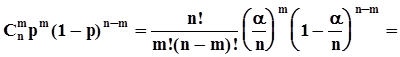
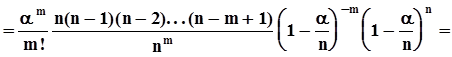
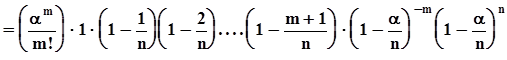 .
.
В полученном выражении первый сомножитель не содержит n.Предел последнего сомножителя при n ®¥равен 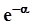 . Пределы остальных сомножителей при n ®¥равны 1. В результате получаем ассимтотическое представление вероятностей из схемы Бернулли или, что то же самое, биномиального распределения в виде
. Пределы остальных сомножителей при n ®¥равны 1. В результате получаем ассимтотическое представление вероятностей из схемы Бернулли или, что то же самое, биномиального распределения в виде 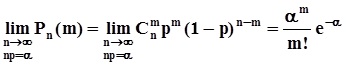 .Этот результат получен Пуассоном и успешно применяется для расчета вероятностей редких событий (при n ®¥вероятность p стремится к 0) при массовых явлениях (испытаниях, опытах).
.Этот результат получен Пуассоном и успешно применяется для расчета вероятностей редких событий (при n ®¥вероятность p стремится к 0) при массовых явлениях (испытаниях, опытах).
Полученные предельные значения вероятностей образуют в совокупности распределение вероятностей случайной величины. В самом деле, 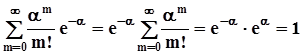 .Это распределение называется распределением Пуассона. Математическое ожидание и дисперсия этой случайной величины равны M[m] = D[M] = a = np.Производящая функция распределения Пуассона:
.Это распределение называется распределением Пуассона. Математическое ожидание и дисперсия этой случайной величины равны M[m] = D[M] = a = np.Производящая функция распределения Пуассона: 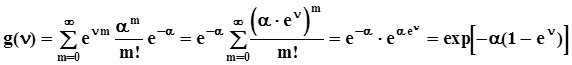 .
.
Локальная теорема Муавра - Лапласа
|
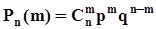 при n ®¥ и p = constаппроксимируются функцией
при n ®¥ и p = constаппроксимируются функцией 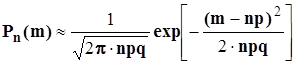 .Эта функция имеет максимум при m = npи симметрична относительно положения этого максимума.
.Эта функция имеет максимум при m = npи симметрична относительно положения этого максимума. 4.Дискретные случайные величины,функция распределения и распределение дискретных случайных величин,числовые характеристики дискретных случайных величин.Дискретные случайные величиныСлучайная величина - функция случайного события, x = f(w). Область определения функции - пространство элементарных исходов W, область значений - все вещественные числа. Дискретная случайная величина - случайная величина, которая может принимать только счетное множество значений.
Распределение вероятностей дискретных случайных величинПусть 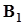 ,
, 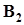 , . . . ,
, . . . , 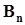 - полная группа непересекающихся событий
- полная группа непересекающихся событий 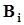 , которые могут возникать при выполнении некоторых испытаний в условиях S. P(
, которые могут возникать при выполнении некоторых испытаний в условиях S. P( 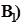 ,
, 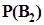 , . . . ,
, . . . , 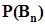 - вероятности событий
- вероятности событий 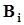 .Пусть также каждому из событий
.Пусть также каждому из событий 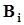 по какому - либо правилу поставлено во взаимно однозначное соответствие вещественное число
по какому - либо правилу поставлено во взаимно однозначное соответствие вещественное число 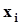 . Так мы определили вещественную функцию случайных событий. При выполнении испытаний эта функция будет принимать значения
. Так мы определили вещественную функцию случайных событий. При выполнении испытаний эта функция будет принимать значения 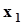 ,
, 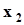 , . . . ,
, . . . , 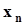 с вероятностями
с вероятностями 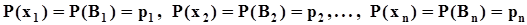 .
.
Таким образом определена дискретная случайная величина x набором значений, которые она может принимать, и набором вероятностей, с которыми она может принимать эти значения: 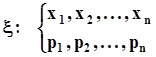 .Векторная запись этого определения экономнее:
.Векторная запись этого определения экономнее: 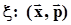 , где
, где 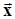 - вектор значений
- вектор значений 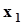 ,
, 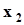 , . . . ,
, . . . , 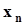 ,
, 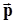 - вектор вероятностей
- вектор вероятностей 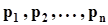 .
.
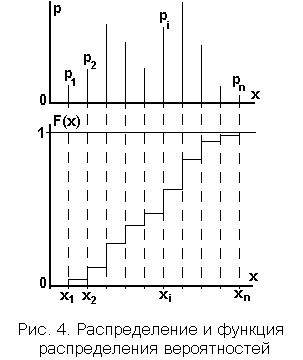 |
Совокупность значений 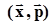 представляет собой наиболее полное описание дискретной случайной величины и называется распределением вероятностей.
представляет собой наиболее полное описание дискретной случайной величины и называется распределением вероятностей.
Поскольку случайные события 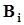 образуют полную группу непересекающихся событий,
образуют полную группу непересекающихся событий, 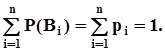
Наряду с распределением вероятностей в теории вероятностей используется еще одна полная характеристика случайных величин, а именно, функция распределения вероятностейF(x):
F(x) = P(x 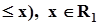 . Числовые характеристики дискретных случайных величинРаспределение вероятностей случайной величины - это максимально полная ее характеристика, но в то же время очень громоздкая. Кроме того вид распределения реальных случайных величин, которые порождаются техническими причинами в измерительных системах, системах автоматизации, в системах передачи и приема информации, чувствителен к неконтролируемым случайным факторам. Поэтому в технических приложениях чаще всего используются не распределения вероятностей, а числовые характеристики расположения случайной величины на числовой оси, разброса ее значений и других свойств.
. Числовые характеристики дискретных случайных величинРаспределение вероятностей случайной величины - это максимально полная ее характеристика, но в то же время очень громоздкая. Кроме того вид распределения реальных случайных величин, которые порождаются техническими причинами в измерительных системах, системах автоматизации, в системах передачи и приема информации, чувствителен к неконтролируемым случайным факторам. Поэтому в технических приложениях чаще всего используются не распределения вероятностей, а числовые характеристики расположения случайной величины на числовой оси, разброса ее значений и других свойств.
В качестве таких характеристик применяются моменты распределения вероятностей. Это название вызывает механические ассоциации, которыми мы будем пользоваться при изложении нижеследующего материала.
Механическая система, моделирующая распределение вероятностей, может быть представлена в виде жесткого невесомого стержня (числовая ось), на которую нанизаны точечные массы, расположенные в точках 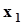 ,
, 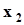 , . . . ,
, . . . , 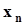 . Значения вероятностей
. Значения вероятностей 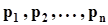 моделируются, как значения массы (или веса) этих точек. Таким образом эти точечные массы придают описанной механической системе вращающий момент относительно начала координат.
моделируются, как значения массы (или веса) этих точек. Таким образом эти точечные массы придают описанной механической системе вращающий момент относительно начала координат.
В качестве характеристики расположения всех значений случайной величины на оси естественно использовать координату центра тяжести описанной механической системы. Как известно из теоретической механики, координата центра тяжести системы определяется из условия равенства моментов: вращающего момента, создаваемого точечными массами, и противодействующего момента, который должна создавать равнодействующая сила, приложенная к центру тяжести.
Итак, пусть 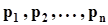 - веса точечных масс, то есть силы, создающие вращающий момент относительно начала координат. Тогда отрезки [0,
- веса точечных масс, то есть силы, создающие вращающий момент относительно начала координат. Тогда отрезки [0, 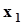 ], [0,
], [0, 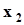 ], . . . , [0,
], . . . , [0, 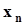 ] - плечи. Равнодействующая сила равна сумме сил, создаваемых точечными массами. Если
] - плечи. Равнодействующая сила равна сумме сил, создаваемых точечными массами. Если 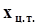 - координата центра тяжести, то отрезок [0,
- координата центра тяжести, то отрезок [0, 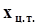 ] - плечо равнодействующей силы. Уравнение моментов имеет вид:
] - плечо равнодействующей силы. Уравнение моментов имеет вид:
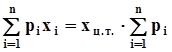 ,
, 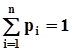 .Отсюда следует, что
.Отсюда следует, что 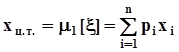 ,
,
где через 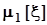 обозначена первая из характеристик распределения вероятностей и самой случайной величины, которая имеет два равноправных названия: математическое ожидание случайной величины x или первый начальный момент случайной величины x. Для обозначения математического ожидания используют также равноправное обозначениеM[x].
обозначена первая из характеристик распределения вероятностей и самой случайной величины, которая имеет два равноправных названия: математическое ожидание случайной величины x или первый начальный момент случайной величины x. Для обозначения математического ожидания используют также равноправное обозначениеM[x].
Рассеяние, разбросанность по числовой оси построенной нами механической системы - аналога распределения вероятностей - не зависит от расположения центра тяжести и характеризуется моментом инерции системы относительно ее центра тяжести. Напомним, что момент инерции точки относительно оси вращения пропорционален массе точки и квадрату ее расстояния от оси. Применительно к распределению вероятностей эта характеристика называется вторым центральным моментом распределения (случайной величины) или дисперсией случайной величины, вычисляется по очевидной формуле для моментов инерции, и имеет несколько равноправных обозначений: 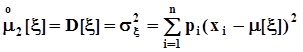 где
где 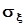 - среднеквадратическое значение (отклонение) случайной величины.Понятно, что если величина не случайна, а потому в любых обстоятельствах может принимать только одно значение с вероятностью 1, то ее дисперсия будет равна нулю.Кружок над обозначением момента означает, что этот момент вычисляется относительно центра тяжести.В теории вероятностей в отличие от механики широко используются начальные и центральные моменты более высокого порядка:
- среднеквадратическое значение (отклонение) случайной величины.Понятно, что если величина не случайна, а потому в любых обстоятельствах может принимать только одно значение с вероятностью 1, то ее дисперсия будет равна нулю.Кружок над обозначением момента означает, что этот момент вычисляется относительно центра тяжести.В теории вероятностей в отличие от механики широко используются начальные и центральные моменты более высокого порядка:
- начальные моменты порядка k : 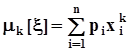 ,
,
- центральные моменты порядкаk: 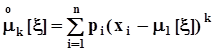 .
.
Найдем несколько полезных соотношений. Вначале вычислим первый центральный момент:
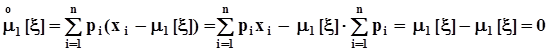 ,
,
чего и следовало ожидать. теперь соотношение между вторыми моментами: начальным и центральным. 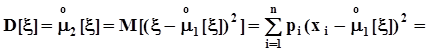
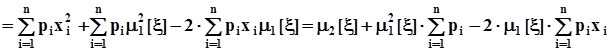 .Поскольку
.Поскольку 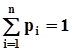 и
и 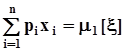 , окончательно получим:
, окончательно получим: 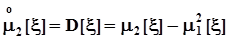 .
.
5.Производящая функция моментов дискретной случайной величины,еесвойства,определение моментов с ее помощью,примеры по заданию экзаменатора.
Производящая функция моментов дискретной случайной величиныПроизводящей функцией моментов случайной величины x называется математическое ожидание функции y(n) = exp(nx), где n - аргумент производящей функции моментов: 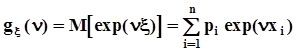 . Производящаяфункциямоментов обладает рядом полезных свойств:1.
. Производящаяфункциямоментов обладает рядом полезных свойств:1. 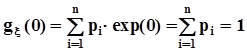 .2. Первая производная от
.2. Первая производная от 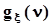 по аргументу n :
по аргументу n : 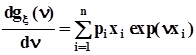 ,при n = 0 получим
,при n = 0 получим 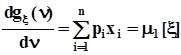 .3. Вторая производная от
.3. Вторая производная от 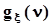 по аргументу n :
по аргументу n : 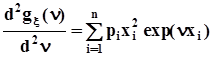 ,при n = 0 получим
,при n = 0 получим 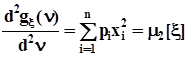 .
.
4.k -ая производная от 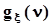 по аргументу n :
по аргументу n : 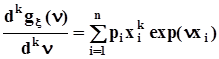 ,при n = 0 получим
,при n = 0 получим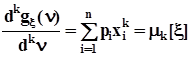 .Таким образом, чтобы получить значение k - ого начального момента, достаточно продифференцировать производящую функцию моментов k раз по n и подставить в полученную производную n = 0. Пример. Написать производящую функцию моментов для биномиального распределения и вычислить математическое ожидание и дисперсию случайной величины, распределенной по биномиальному закону.
.Таким образом, чтобы получить значение k - ого начального момента, достаточно продифференцировать производящую функцию моментов k раз по n и подставить в полученную производную n = 0. Пример. Написать производящую функцию моментов для биномиального распределения и вычислить математическое ожидание и дисперсию случайной величины, распределенной по биномиальному закону.
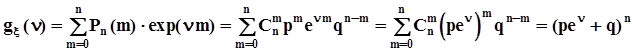 Первая производная от
Первая производная от 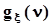 по n
по n 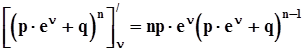 .Вторая производная от
.Вторая производная от 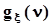 по n
по n 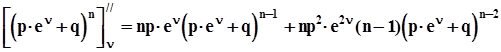 .Вычислим эти производные при n = 0:
.Вычислим эти производные при n = 0: 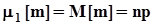 ,
, 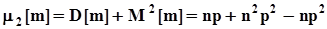 .Окончательно получим: M[m]=np, D[m]=np(1-p) = npq.Сопоставляя полученное выражение для математического ожидания числа появления события A в испытаниях по схеме Бернулли с наиболее вероятным значением этого числа, видим, что они совпадают.
.Окончательно получим: M[m]=np, D[m]=np(1-p) = npq.Сопоставляя полученное выражение для математического ожидания числа появления события A в испытаниях по схеме Бернулли с наиболее вероятным значением этого числа, видим, что они совпадают.
6.Двумерные дискретные случайные величины,распределениявероятностей,моменты,маргинальные распределения, производящие функции моментов.Двумерные дискретные случайные величины.
Распределение вероятностейБудем рассматривать двумерную случайную величину, как двумерный случайный вектор 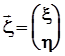 .Компонентами вектора
.Компонентами вектора  являются дискретные случайные величиныx и h, которые могут принимать значения
являются дискретные случайные величиныx и h, которые могут принимать значения 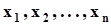 и
и 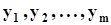 соответственно. Реализации вектора
соответственно. Реализации вектора  будем обозначать через
будем обозначать через  .При каждом испытании компоненты вектора
.При каждом испытании компоненты вектора  могут принимать значения
могут принимать значения 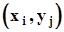 с вероятностью совместного осуществления двух событий
с вероятностью совместного осуществления двух событий 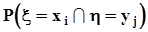 . В дальнейшем мы будем пользоваться упрощенными обозначениями этой вероятности в виде
. В дальнейшем мы будем пользоваться упрощенными обозначениями этой вероятности в виде 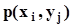 или еще проще -
или еще проще - 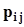 . Кроме того заметим, что события
. Кроме того заметим, что события 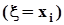 образуют полную группу попарно несовместных событий. То же самое можно утверждать и о событиях
образуют полную группу попарно несовместных событий. То же самое можно утверждать и о событиях 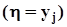 .Представим совместное распределение вероятностей
.Представим совместное распределение вероятностей 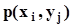 в виде следующей таблицы.
в виде следующей таблицы.
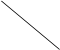 h x h x | 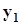 | 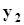 | . . . | 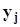 | . . . | 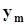 | |
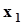 | 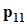 | 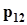 | . . . | 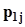 | . . . | 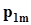 | 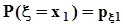 |
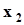 | 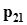 | 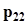 | . . . | 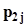 | . . . | 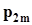 | 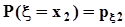 |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
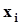 | 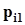 | 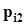 | . . . | 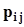 | . . . | 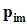 | 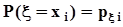 |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
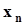 | 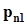 | 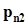 | . . . | 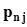 | . . . | 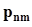 | 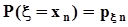 |
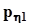 | 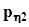 | . . . | 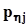 | . . . | 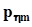 |
События 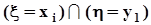 ,
, 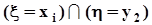 , ...,
, ..., 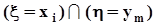 не пересекаются, а их объединение есть не что иное, как событие
не пересекаются, а их объединение есть не что иное, как событие 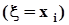 . Поэтому, суммируя элементы этой таблицы по строкам, в соответствии с аксиомой аддитивности (см. п. 1.2.2) получим значения вероятностей
. Поэтому, суммируя элементы этой таблицы по строкам, в соответствии с аксиомой аддитивности (см. п. 1.2.2) получим значения вероятностей 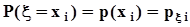 . По этой же причине суммирование элементов таблицы по столбцам даст значения вероятностей
. По этой же причине суммирование элементов таблицы по столбцам даст значения вероятностей 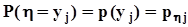 . Тот же результат мы получим, если определим условные вероятности
. Тот же результат мы получим, если определим условные вероятности 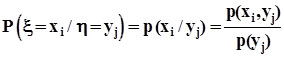
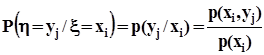
и поскольку события 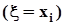 и
и 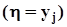 образуют полные группы попарно несовместных событий, применим формулу полной вероятности
образуют полные группы попарно несовместных событий, применим формулу полной вероятности 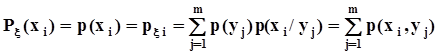
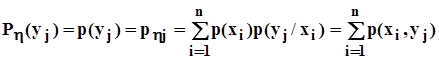 .
.
Сумма всех вероятностей равна 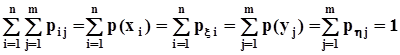 .
.
Тем самым мы получили маргинальные (частные) распределения случайных компонент x и h
, .
Признак независимости случайных компонент вектора  : случайные компоненты x и hвектора
: случайные компоненты x и hвектора  независимы тогда и только тогда, когда их совместное распределение вероятностей может быть представлено, как произведение маргинальных (частных) распределений (см. также п. 1.2.3):
независимы тогда и только тогда, когда их совместное распределение вероятностей может быть представлено, как произведение маргинальных (частных) распределений (см. также п. 1.2.3):
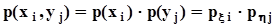 . Числовые характеристики
. Числовые характеристики
Числовые характеристики, а именно, моменты отдельных составляющих вектора  определяются через маргинальные (частные) распределения точно так же, как это делалось для одномерной (скалярной) дискретной случайной величины:
определяются через маргинальные (частные) распределения точно так же, как это делалось для одномерной (скалярной) дискретной случайной величины:
-начальные моменты k - го порядка: 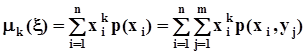 ,
, 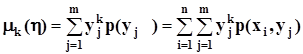 ,и, в частности, математические ожидания
,и, в частности, математические ожидания 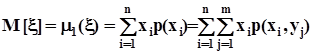 ,
, 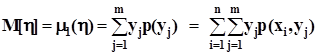 .
.
- центральные моменты k - го порядка 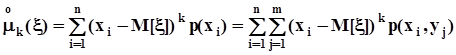
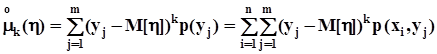 ,
,
и, в частности, дисперсии
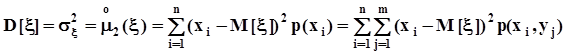
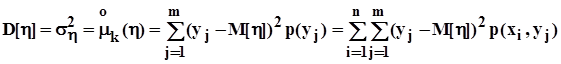 .
.
Для составляющих случайного вектора определены смешанныемоменты:
- начальные моменты порядка k, r
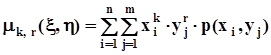 ,
,
- центральные моменты порядка k, r
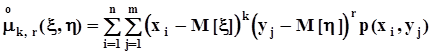 . Особенное значение для дальнейшего имеет центральный смешанный момент порядка 1, 1,который называется корреляционным моментом или ковариацией:
. Особенное значение для дальнейшего имеет центральный смешанный момент порядка 1, 1,который называется корреляционным моментом или ковариацией:
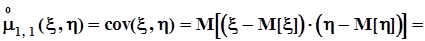
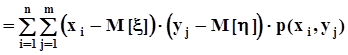 .Для того, чтобы установить соотношение между центральным и начальным смешанными моментами раскроем скобки в последнем выражении и выполним несложные преобразования:
.Для того, чтобы установить соотношение между центральным и начальным смешанными моментами раскроем скобки в последнем выражении и выполним несложные преобразования:
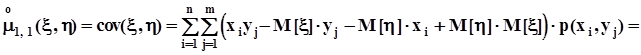
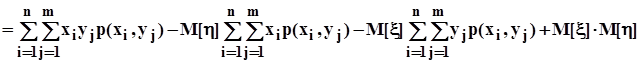 .Окончательно получим:
.Окончательно получим: 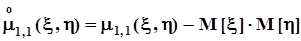 .
.
Если x и hнезависимы, то 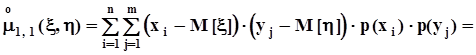
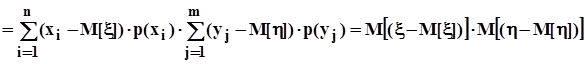 .
.
Но, как было установлено в п. 1.3.3, 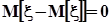 и
и 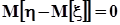 , поэтому центральный смешанный момент
, поэтому центральный смешанный момент 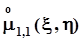 независимых случайных величин равен нулю. Однако, из того, что
независимых случайных величин равен нулю. Однако, из того, что 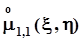 =0 независимость случайных величин x и h ,вообще говоря,не следует. О случайных величинах, корреляционный момент которых равен нулю, говорят, что они некоррелированы. Для оценки степени коррелированности случайных величин в приложениях удобнее использовать безразмерный коэффициент корреляции
=0 независимость случайных величин x и h ,вообще говоря,не следует. О случайных величинах, корреляционный момент которых равен нулю, говорят, что они некоррелированы. Для оценки степени коррелированности случайных величин в приложениях удобнее использовать безразмерный коэффициент корреляции 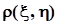 , значение которого не зависит от масштаба, в котором выражены значения случайных величин:
, значение которого не зависит от масштаба, в котором выражены значения случайных величин:
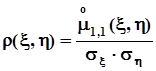 . С целью определения диапазона значений коэффициента корреляции рассмотрим крайний случай взаимнооднозначной зависимости между x и h,а именно, допустим, что h = ax + b. Другой крайний случай, а именно, независимость x и hрассмотрен выше в настоящем пункте.Из предположенной линейной зависимости следует :
. С целью определения диапазона значений коэффициента корреляции рассмотрим крайний случай взаимнооднозначной зависимости между x и h,а именно, допустим, что h = ax + b. Другой крайний случай, а именно, независимость x и hрассмотрен выше в настоящем пункте.Из предположенной линейной зависимости следует : 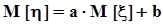 ,
, 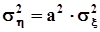 ,
, 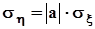
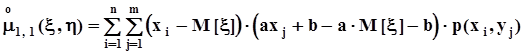 . После простых преобразований получим:
. После простых преобразований получим: 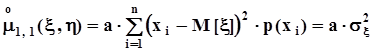 ,
, 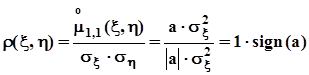 .Таким образом, мы установили, что коэффициент корреляции не превосходит единицы по абсолютной величине:
.Таким образом, мы установили, что коэффициент корреляции не превосходит единицы по абсолютной величине: 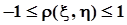 .
.
Математическое ожидание случайного вектора - вектор, составляющие (компоненты) которого суть математические ожидания соответствующих компонент:
 .
.
Дисперсии компонент случайного вектора  и их ковариации объединяют в ковариационную матрицу следующим образом:
и их ковариации объединяют в ковариационную матрицу следующим образом:
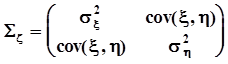 .
.
В теории вероятностей часто используется корреляционная матрица, которая получается из ковариационной матрицы путем деления ее элементов на произведение среднеквадратических значений:
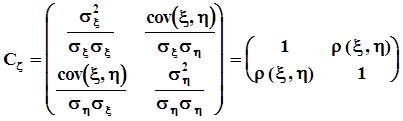 .
.
Эти матрицы симметричны и неотрицательно определены. Если компоненты случайного вектора независимы или хотя бы некоррелированы, матрицы 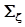 и
и 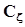 диагональны. Математическое определение ковариационной матрицы:
диагональны. Математическое определение ковариационной матрицы:
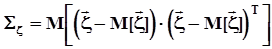 ,
,
где ‘т’ - символ транспонирования.
Раскроем это выражение.
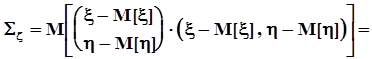
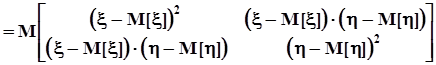 .
.
Математическое ожидание случайной матрицы есть матрица, элементы которой суть математические ожидания:
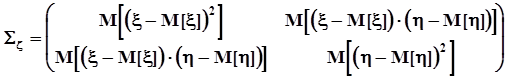 =
=
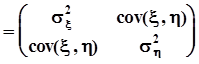 Производящая функция моментов двумерного случайного вектора
Производящая функция моментов двумерного случайного вектора
Математическое определение производящей функции моментов: 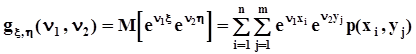 .Свойства этой функции аналогичны свойствам производящей функции моментов одномерной случайной величины, которые были установлены ранее в п. 1.3.5.
.Свойства этой функции аналогичны свойствам производящей функции моментов одномерной случайной величины, которые были установлены ранее в п. 1.3.5.
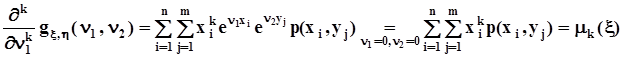 ,
,
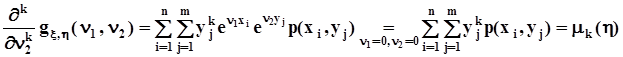 .
.
Дополнительно к этим свойствам производящие функции моментов двумерных случайных величин позволяют находить смешанные начальные моменты:
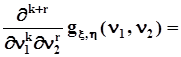
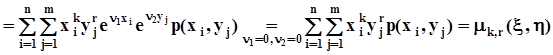 .
.
Найдем производящую функцию моментов линейной комбинации двух независимых случайных величин 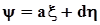 :
:
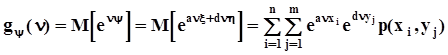 .В силу независимости x и h совместное распределение
.В силу независимости x и h совместное распределение 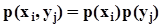 , поэтому
, поэтому 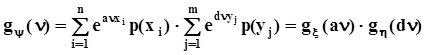 .При a = d = 1 получим удобное выражение
.При a = d = 1 получим удобное выражение 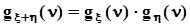 , из которого следует, что производящая функция моментов суммы двух независимых случайных величин равна произведению производящих функций моментов слагаемых.
, из которого следует, что производящая функция моментов суммы двух независимых случайных величин равна произведению производящих функций моментов слагаемых.

