Тогда ее решение имеет вид
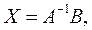 | (12) |
если определитель системы отличен от нуля.
Если система линейных уравнений с n неизвестными совместна, а ранг матрицы системы меньше числа неизвестных, т. е.
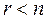 | (13) |
то система имеет бесконечное множество решений. Свободные n – r неизвестных выбираются произвольно, а главные r неизвестных определяются единственным образом через свободные неизвестные.
9. Вектор-столбец
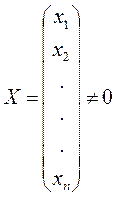
называется собственным вектором квадратной матрицы А п-го порядка, соответствующим собственному значению l, если он удовлетворяет матричному уравнению
АХ=lХ, или (А - lЕ)Х = 0
Здесь Е - единичная матрица n-го порядка, а 0 - нулевой вектор-столбец. При условии, что вектор Х¹О, получаем характеристическое уравнение для определения собственных значений l:
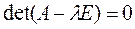 | (14) |
Координаты собственного вектора Xi соответствующего собственному значению li, являются решением системы уравнений
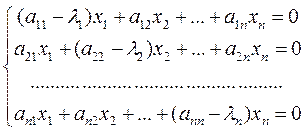 | (15) |
Собственный вектор определяется с точностью до постоянного множителя.
Пример 1. По координатам вершин пирамиды А1 (3; -2; 2), А2 (1; —3; 1), A3 (2; 0; 4), А4 (6; -4; 6) найти: 1) длины ребер А1Аг и А1А3; 2) угол между ребрами А1Аг и А1А3; 3) площадь грани А1АгА3 ; 4) объем пирамиды
Решение. 1) Находим векторы А1Аг и А1А3:
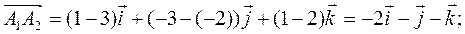
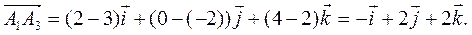
Длины этих векторов, т. е. длины ребер А1Аг и А1А3, таковы:
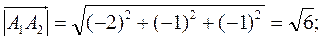
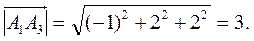
2) Скалярное произведение векторов 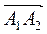 и
и 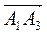 находим по формуле (1):
находим по формуле (1):
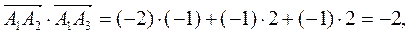
а косинус угла между ними — по формуле (5):
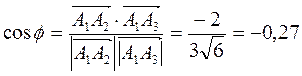
Отсюда следует, что 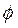 — тупой угол, равный
— тупой угол, равный 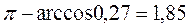 рад с точностью до 0,01. Это и есть искомый угол между ребрами А1Аг и А1А3.
рад с точностью до 0,01. Это и есть искомый угол между ребрами А1Аг и А1А3.
3) Площадь грани А1АгА3 равна половине площади параллелограмма, построенного на векторах 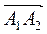 и
и 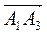 ,т. е. половине модуля векторного произведения этих векторов [см. формулу (2)]:
,т. е. половине модуля векторного произведения этих векторов [см. формулу (2)]:
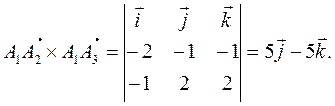
Здесь определитель вычисляется с помощью разложения по первой строке. Следовательно,
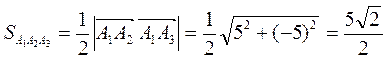
4) Объем V пирамиды равен 1/6 объема параллелепипеда, построенного на векторах 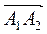 ,
, 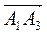 ,
, 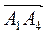 . Вектор
. Вектор 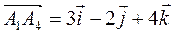 . Используя формулу (3), получаем
. Используя формулу (3), получаем
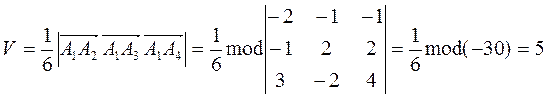
Пример 2. Найти угол между плоскостью Р1, проходящей через точки А1 (2; —4; 1), А2 (—1; 2; 0), А3(0; —2; 3), и плоскостью Р2 , заданной уравнением 5х+2у-3z=0.
Решение. Уравнение плоскости Р1 находим по формуле (4):
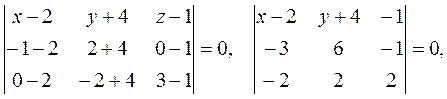
т. е.
7(х-2)+4(у+4)+3(z-1)=0, 7x+4y+3z=1
По уравнениям плоскостей определяем их нормальные векторы: 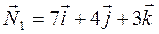 ,
, 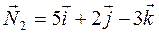 . Угол
. Угол 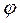 между плоскостями
между плоскостями 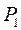 и
и 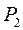 находим по формуле (5):
находим по формуле (5):
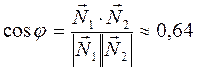
откуда 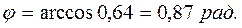
Пример 3. Составить уравнение прямой, проходящей через точки А1 (4; -3; 1) и А2 (5; -3; 0).
Решение. Используя формулу (6), получаем
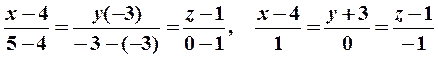
Равенство нулю знаменателя второй дроби означает, что прямая принадлежит плоскости y = -3.
Пример 4. С помощью формул Крамера найти решение системы линейных уравнений
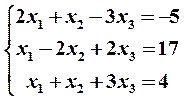 | (16) |
Решение. Вычислим определитель системы
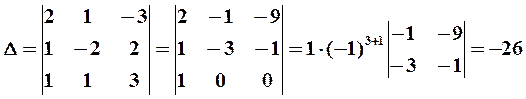
Так как 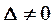 , то решение системы может быть найдено по формулам Крамера (11). Для этого найдем
, то решение системы может быть найдено по формулам Крамера (11). Для этого найдем 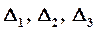 :
:

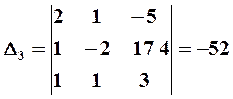
Подставляя найденные значения определителей в формулы (11), получаем искомое решение системы: 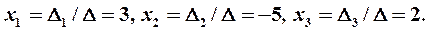
Пример 5. Найти решение системы примера 4 с помощью обратной матрицы.
Решение. Здесь
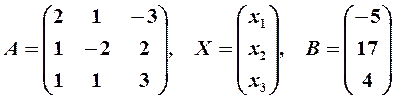
Так как определитель матрицы системы отличен от нуля (см. пример 4): 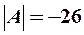 , то матрица А имеет обратную. Для нахождения обратной матрицы
, то матрица А имеет обратную. Для нахождения обратной матрицы 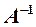 вычислим алгебраические дополнения элементов матрицы А:
вычислим алгебраические дополнения элементов матрицы А:
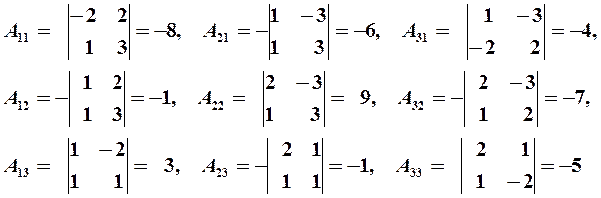
Согласно формуле (9), матрица 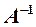 ,обратная к А,имеет вид
,обратная к А,имеет вид
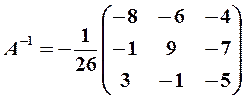
Проверим правильность вычисления 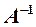 ,исходя из определения обратной матрицы (8) и используя формулу (7):
,исходя из определения обратной матрицы (8) и используя формулу (7):
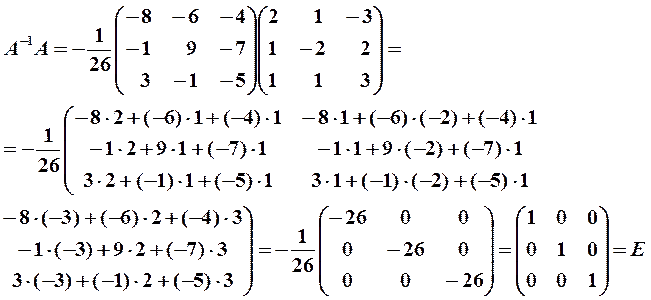
Матричное решение системы (16) в силу формулы (12) имеет вид
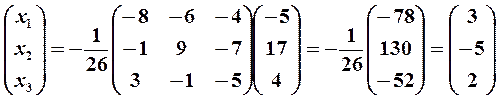
откуда следует (из условия равенства двух матриц), что х1 = 3, х2= - 5, х3 = 2.
Пример 6. Найти решение однородной системы линейных уравнений
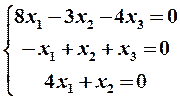 | (17) |
Решение. Однородная система имеет нетривиальное решение, если ранг матрицы системы
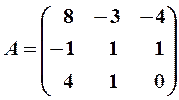
меньше числа неизвестных [см. формулу (13)]. Приведем матрицу А к каноническому виду 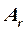 путем элементарных преобразований. Прибавляя к 1-му столбцу 3-й, а из 3-го вычитая 2-й, получаем
путем элементарных преобразований. Прибавляя к 1-му столбцу 3-й, а из 3-го вычитая 2-й, получаем
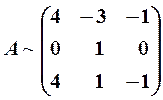
Умножим 1-й столбец на 1/4, а затем вычтем из 3-й строки 1-ю:
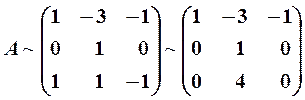
Из 3-й строки вычтем 2-ю, умноженную на 4, а затем ко 2-му и 3-му столбцам прибавим 1-й столбец, умноженный соответственно на 3 и 1:
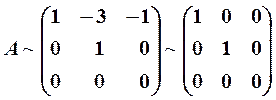
Таким образом, ранг матрицы Аравен 2 и система (17) имеет нетривиальное решение. Примем за главные неизвестные 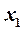 и
и 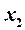 . Тогда система (17) сводится ксистеме двух уравнений
. Тогда система (17) сводится ксистеме двух уравнений
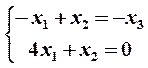
решение которой имеет вид 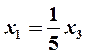 ,
, 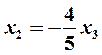 . Придавал свободному неизвестному
. Придавал свободному неизвестному 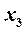 произвольные значения
произвольные значения 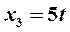 , получаем решение системы (17) ввиде
, получаем решение системы (17) ввиде 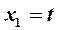 ,
, 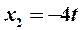 ,
, 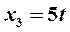 .
.
Пример 7. Определить собственные значения и собственные векторы матрицы
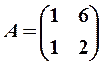
Решение. Характеристическое уравнение для данной матрицы имеет вид (14):
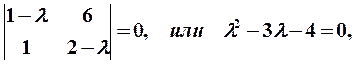
откуда следует, что матрица Аимеет два собственных значения 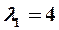 и
и 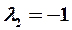 . Собственный вектор
. Собственный вектор 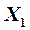 ,соответствующий
,соответствующий 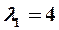 , определяется из системы уравнений вида (15)
, определяется из системы уравнений вида (15)
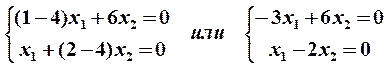
которая сводится к одному уравнению 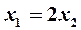 . Полагая
. Полагая 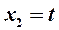 , получаем решение в виде
, получаем решение в виде 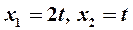 . Следовательно, первый собственный вектор есть
. Следовательно, первый собственный вектор есть 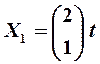 .
.
Второй собственный вектор 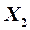 , соответствующий собственному значению
, соответствующий собственному значению 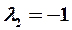 , определяется из системы уравнений вида (15):
, определяется из системы уравнений вида (15):
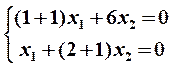
Эта система уравнений также сводится к одному уравнению 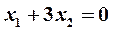 ; полагая
; полагая 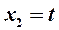 , запишем ее решение в виде
, запишем ее решение в виде 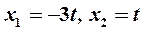 . Следовательно, второй собственный вектор есть
. Следовательно, второй собственный вектор есть 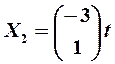 .
.
Таким образом, матрица Аимеет два собственных различных значение 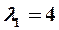 и
и 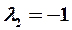 и два собственных вектора, равных (с точностью до постоянного множителя)
и два собственных вектора, равных (с точностью до постоянного множителя) 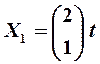 ,
, 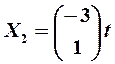 .
.
ВВЕДЕНИЕ В АНАЛИЗ.
Основные теоретические сведения
1. Прямоугольные координаты (х, у)точки Ми ее полярные координаты 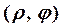 связаны соотношениями
связаны соотношениями
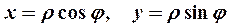 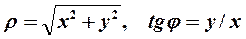 | (1) |
где 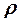 - полярный радиус, а
- полярный радиус, а 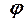 - полярный угол точки М(рис. 3).
- полярный угол точки М(рис. 3).
2. Определение конечного предела функции в точке: число А называется пределом функции 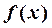 при
при 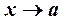 ,если для любого
,если для любого 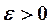 найдется
найдется 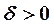 такое, что
такое, что 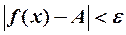 при
при 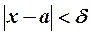 . Обозначение:
. Обозначение: 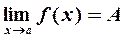 или
или 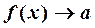 при
при 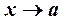 .
.
Функция 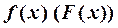 называется бесконечно малой (бесконечно большой) при
называется бесконечно малой (бесконечно большой) при 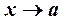 ,если
,если 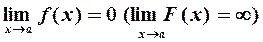 .
.
Две функции 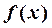 и
и 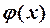 , одновременно стремящиеся к нулю или бесконечности при
, одновременно стремящиеся к нулю или бесконечности при 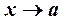 , называются эквивалентными, если
, называются эквивалентными, если 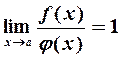 . Обозначение:
. Обозначение: 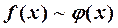 .
.
Предел отношения бесконечно малых (бесконечно больших) функций не изменится, если каждую из них заменить эквивалентной ей функцией, т. е.
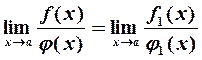 | (2) |
если 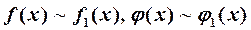 .
.
3. К основным элементарным функциям относятся: 1) степенная функция 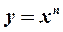 ; 2)показательна функция
; 2)показательна функция 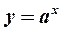 ;3) логарифмическая функция
;3) логарифмическая функция 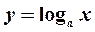 ; 4) тригонометрические функции:
; 4) тригонометрические функции: 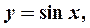
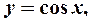
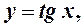
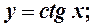 5) обратные тригонометрические функции:
5) обратные тригонометрические функции: 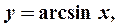
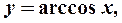
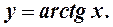
Предел элементарной функции в точке области ее определения равен частному значению функции в этой точке: 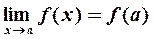 .
.
 |
Рис. 3
Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям вида 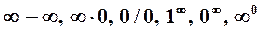 . Элементарными приемами раскрытия неопределенностей являются: 1) сокращение на множитель, создающий неопределенность; 2) деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при
. Элементарными приемами раскрытия неопределенностей являются: 1) сокращение на множитель, создающий неопределенность; 2) деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при 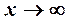 3) применение эквивалентных бесконечно малых и бесконечно больших; 4) использование двух замечательных пределов:
3) применение эквивалентных бесконечно малых и бесконечно больших; 4) использование двух замечательных пределов:
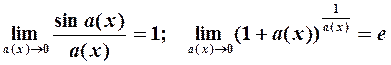 | (3) |
Отметим также, что
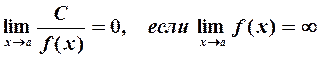
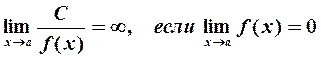
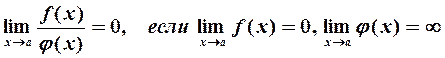
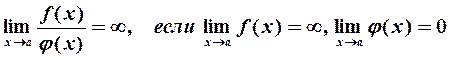
4. Функция/(х) называется непрерывной в точке 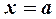 , если:
, если:
1) частное значение функции в точке 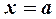 равно
равно 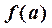 ;
;
2) существуют конечные односторонние пределы функции
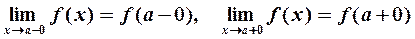 | (4) |
3) односторонние пределы равны:
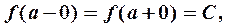 | (5) |
4) предельное значение функции в точке 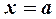 равно ее частному значению
равно ее частному значению 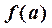
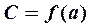 | (6) |
Обозначение: 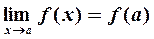
Точка 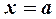 называется точкой устранимого разрыва, если
называется точкой устранимого разрыва, если 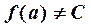 [нарушается условие (6)].
[нарушается условие (6)].
Точка 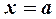 называется точкой разрыва первого рода, если оба односторонних предела конечны, но
называется точкой разрыва первого рода, если оба односторонних предела конечны, но 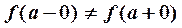 [нарушается условие (5)].
[нарушается условие (5)].
Точка 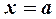 называется точкой разрыва второго рода, если хотя бы один из односторонних пределов равен бесконечности или не существует [нарушается условие (4)].
называется точкой разрыва второго рода, если хотя бы один из односторонних пределов равен бесконечности или не существует [нарушается условие (4)].
5. Выражение вида 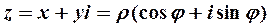 называется комплексным числом (валгебраической и тригонометрическойформе соответственно).Здесь
называется комплексным числом (валгебраической и тригонометрическойформе соответственно).Здесь 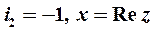 — действительная часть, а
— действительная часть, а 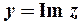 — мнимая часть комплексного числа
— мнимая часть комплексного числа 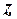 ;
; 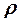 и
и 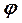 — модуль и аргумент числа
— модуль и аргумент числа 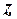 .
.
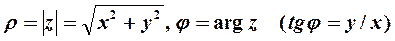 | (7) |
Комплексные числа изображаются точками на комплексной плоскости (рис. 4).
Извлечение корня n-й степени (n — натуральное число) из числа 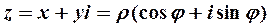 (
( 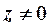 ) производится по формуле
) производится по формуле
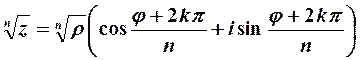 | (8) |
где 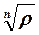 — арифметический корень из модуля
— арифметический корень из модуля 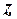 , a
, a 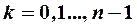 .
.
|
Рис. 4
Пример 1. Найти полярные координаты точки 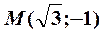 (рис. 5).
(рис. 5).
Решение. Используя формулы (1), находим полярный радиус и полярный
угол точки М:
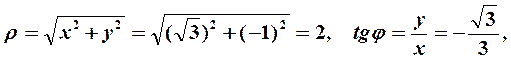
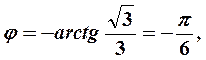
так как точка Млежит в IV четверти.
Пример 2. Построить по точкам график 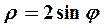 в полярной системе координат. Найти уравнение полученной кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полуось Ох — с полярной осью. Определить вид кривой.
в полярной системе координат. Найти уравнение полученной кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полуось Ох — с полярной осью. Определить вид кривой.
Решение. Так как полярный радиус не отрицателен, т. е. 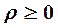 , то
, то 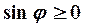 , откуда
, откуда 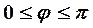 ; значит, вся кривая расположена в верхней полуплоскости. Составим вспомогательную таблицу:
; значит, вся кривая расположена в верхней полуплоскости. Составим вспомогательную таблицу:
| Номера точек | |||||||||
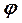 | p/8 | p/4 | 3p/8 | p/2 | 5p/8 | 3p/4 | 7p/8 | p | |
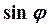 | 0,38 | 0,71 | 0,92 | 0,92 | 0,71 | 0,38 | |||
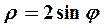 | 0,76 | 1,42 | 1,84 | 1,84 | 1,42 | 0,76 |
Для построения кривой на луче, проведенном из полюса под углом 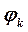 , откладываем соответствующее значение полярного радиуса
, откладываем соответствующее значение полярного радиуса 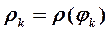 и соединяем полученные точки (рис. 6).
и соединяем полученные точки (рис. 6).
Найдем уравнение кривой 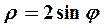 в прямоугольной системе координат. Для этого заменим
в прямоугольной системе координат. Для этого заменим 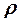 и
и 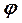 их выражениями через
их выражениями через 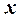 и
и 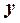 по формулам (1):
по формулам (1):
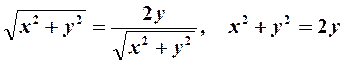
Окончательно имеем 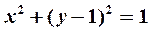 , т. е. рассматриваемое уравнение выражает окружность с центром в точке (0; 1) и единичным радиусом.
, т. е. рассматриваемое уравнение выражает окружность с центром в точке (0; 1) и единичным радиусом.
Пример 3. Найти 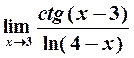
Решение. Подставляя вместо 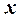 его предельное значение, равное 3, получаем в числителе бесконечно большую, а в знаменателе — бесконечно малую функцию:
его предельное значение, равное 3, получаем в числителе бесконечно большую, а в знаменателе — бесконечно малую функцию:
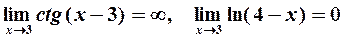
Поэтому 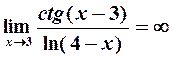
Пример 4. Найти 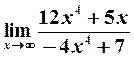
Решение. Подстановка предельного значения аргумента приводит к неопределенности вида 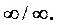 Так как под знаком предела стоит отношение двух многочленов, то разделим числитель и знаменатель на старшую степень аргумента, т. е. на
Так как под знаком предела стоит отношение двух многочленов, то разделим числитель и знаменатель на старшую степень аргумента, т. е. на 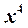 . В результате получим
. В результате получим
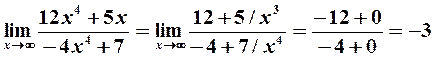
поскольку при 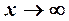 функции
функции 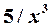 и
и 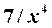 являются бесконечно малыми.
являются бесконечно малыми.
Пример 5. Найти 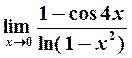
Решение. Для раскрытия получающейся здесь неопределенности вида 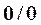 используем метод замены бесконечно малых эквивалентными. Так как при
используем метод замены бесконечно малых эквивалентными. Так как при 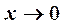
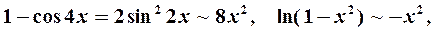 то на основании формулы (2) находим
то на основании формулы (2) находим
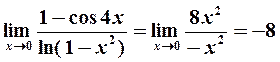
Пример 6. Найти 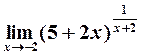 .
.
Решение. Подстановка 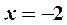 приводит к неопределенности
приводит к неопределенности 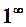 . Произведем замену переменных:
. Произведем замену переменных: 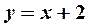 ,
, 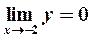 . Тогда
. Тогда
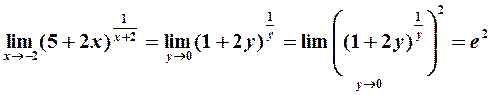
Здесь использован второй замечательный предел (3).
Пример 7. Указать слагаемое, эквивалентное всей сумме 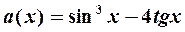 при
при 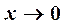
Решение. Очевидно, что при 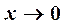 оба слагаемых являются бесконечно малыми. Найдем предел отношения суммы к каждому из слагаемых, используя замену бесконечно малых эквивалентными:
оба слагаемых являются бесконечно малыми. Найдем предел отношения суммы к каждому из слагаемых, используя замену бесконечно малых эквивалентными:
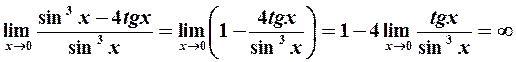
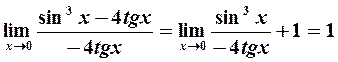
Следовательно, функция 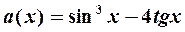 эквивалентна при
эквивалентна при 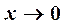 второму слагаемому.
второму слагаемому.
Пример 8. Исследовать функцию
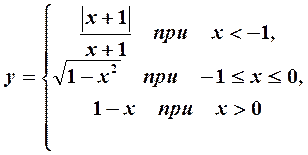
на непрерывность; найти точки разрыва функции и определить их тип. Построить схематический график функции.
Решение. Так как данная функция определена на всей числовой оси, то «подозрительными на разрыв» являются те точки, в которых изменяется аналитическое выражение функции, т. е. точки 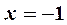 и
и 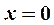 . Вычислим односторонние пределы в этих точках.
. Вычислим односторонние пределы в этих точках.
Для точки 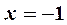 имеем:
имеем:
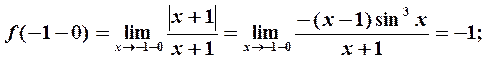
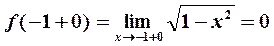
Односторонние пределы функции в точке 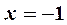 существуют, но не равны между собой. Следовательно, эта точка является точкой разрыва первого рода.
существуют, но не равны между собой. Следовательно, эта точка является точкой разрыва первого рода.
Для точки 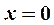 получаем
получаем
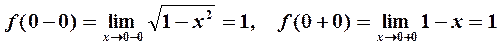
Односторонние пределы функции при 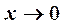 равны между собой и равны частному значению функции
равны между собой и равны частному значению функции 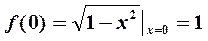 . Следовательно, исследуемая точка является точкой непрерывности.
. Следовательно, исследуемая точка является точкой непрерывности.
График данной функции приведен на рис. 7.
Пример 9. Изобразить на комплексной плоскости числа: 1) 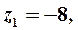 2)
2) 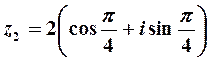 . Записать число
. Записать число 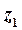 в тригонометрической, а число
в тригонометрической, а число 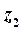 в алгебраической форме.
в алгебраической форме.
Решение. 1) Для числа 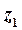 имеем
имеем 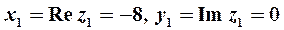 . Откладывая по оси
. Откладывая по оси 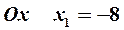 , а по оси
, а по оси 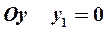 , получаем точку комплексной плоскости, соответствующую числу
, получаем точку комплексной плоскости, соответствующую числу 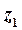 (рис. 8). Модуль этого числа находим по формуле (7):
(рис. 8). Модуль этого числа находим по формуле (7):

Рис. 7 Рис. 8
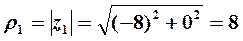 . Аргумент определяем из равенства
. Аргумент определяем из равенства 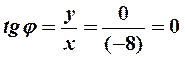 . Так как число
. Так как число 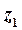 находится в левой полуплоскости, то его аргумент
находится в левой полуплоскости, то его аргумент 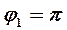 . Тригонометрическая форма числа
. Тригонометрическая форма числа 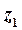 имеет вид
имеет вид 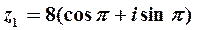 .
.
2) Модуль числа 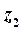 равен
равен 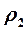 , а аргумент
, а аргумент 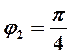 . Для его изображения на
. Для его изображения на
комплексной плоскости проводим из полюса луч под углом 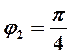 кполярной оси и откладываем на нем отрезок длиной
кполярной оси и откладываем на нем отрезок длиной 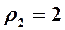 . Полученная точка соответствует числу
. Полученная точка соответствует числу 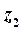 (рис. 8). Его действительная часть
(рис. 8). Его действительная часть 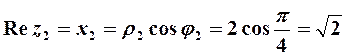 , а мнимая часть
, а мнимая часть 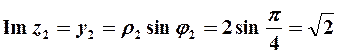 . Таким образом, алгебраическая форма числа
. Таким образом, алгебраическая форма числа 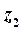 имеет вид
имеет вид 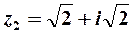 .
.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Основные теоретические сведения
1. Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций (неопределенность 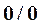 или
или 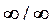 ) равен пределу отношения их производных:
) равен пределу отношения их производных:
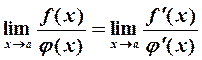 | (1) |
если предел справа существует.
2. Если в некоторой окрестности точки 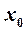 выполняется неравенство
выполняется неравенство 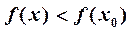 или
или 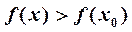 , то точка
, то точка 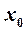 называется точкой экстремума функции
называется точкой экстремума функции 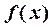 (соответственно точкой максимума или минимума). Необходимое условие экстремума: если
(соответственно точкой максимума или минимума). Необходимое условие экстремума: если 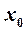 — экстремальная точка функции
— экстремальная точка функции 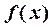 , то первая производная
, то первая производная 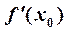 либо равна нулю или бесконечности, либо не существует. Достаточное условие экстремума:
либо равна нулю или бесконечности, либо не существует. Достаточное условие экстремума: 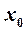 является экстремальной точкой функции
является экстремальной точкой функции 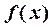 , если ее первая производная
, если ее первая производная 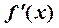 меняет знак при переходе через точку
меняет знак при переходе через точку 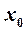 : с плюса на минус — при максимуме, с минуса на плюс — при минимуме.
: с плюса на минус — при максимуме, с минуса на плюс — при минимуме.
3. Точка 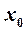 называется точкой перегиба кривой
называется точкой перегиба кривой 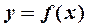 , если при переходе через точку
, если при переходе через точку 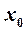 меняется направление выпуклости. Необходимое условие точки перегиба: если
меняется направление выпуклости. Необходимое условие точки перегиба: если 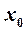 — точка перегиба кривой
— точка перегиба кривой 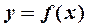 , то вторая производная
, то вторая производная 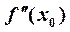 либо равна нулю или бесконечности, либо не существует. Достаточное условие точки перегиба:
либо равна нулю или бесконечности, либо не существует. Достаточное условие точки перегиба: 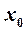 является точкой перегиба кривой
является точкой перегиба кривой 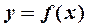 , если при переходе через точку
, если при переходе через точку 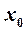 вторая производная
вторая производная 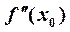 меняет знак,
меняет знак,
4. Прямая 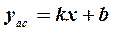 называется наклонной асимптотой кривой
называется наклонной асимптотой кривой 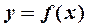 , если расстояние от точки
, если расстояние от точки 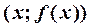 кривой до этой прямой стремится к нулю при
кривой до этой прямой стремится к нулю при 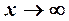 . При этом
. При этом
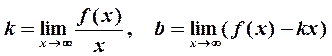 | (2) |
При 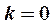 имеем горизонтальную асимптоту:
имеем горизонтальную асимптоту: 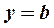 .
.
Если
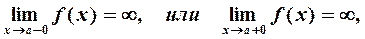 | (3) |
то прямая 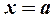 называется вертикальной асимптотой,
называется вертикальной асимптотой,
4. Общая схема исследования функции и построения ее графика.
I. Элементарное исследование:
1) найти область определения функция;
2) исследовать функцию на симметричность и периодичность;
3) вычислить предельные значения функции в ее граничных точках;
4) выяснить существование асимптот;
5) определить, если это не вызовет особых затруднения, точки пересечения
графика функция с координатными осями;
6) сделать эскиз графика функции, используя полученные результаты.
II. Исследование графика функции по первой производной:
1) найти решения уравнений 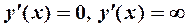 и
и 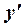 не существует;
не существует;
2) точки, «подозрительные» на экстремум, исследовать с помощью достаточного условия экстремума, определить вид экстремума;
3) вычислить значения функции в точках экстремума;
4) найти интервалы монотонности функции;
5) нанести на эскиз графика экстремальные точки;
6) уточнить вид графика функции согласно полученным результатам.
III. Исследование графика функции по второй производной:
1) найти решения уравнений 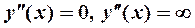 и
и 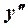 не существует;
не существует;
2) точки, «подозрительные» на перегиб, исследовать с помощью достаточного условия;
3) вычислить значения функции в точках перегиба;
4) найти интервалы выпуклости и вогнутости графика функции;
5) нанести на эскиз графика точки перегиба;
6) окончательно построить график функции.
Если исследование цроведено без ошибок, то результаты всех этапов должны согласовываться друг с другом. Если же согласование отсутствует, необходимо проверить правильность результатов отдельных этапов и исправить найденные ошибки.
6. Частной производной первого порядка функции нескольких переменных 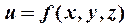 по аргументу
по аргументу 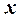 называется предел
называется предел
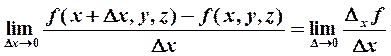 | (4) |
(приращение получает только один аргумент 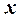 ). Обозначение:
). Обозначение: 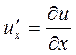 . Отыскание частной производной
. Отыскание частной производной 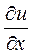 сводится к дифференцированию функции одной переменной
сводится к дифференцированию функции одной переменной 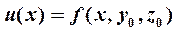 , полученной при фиксировании аргументов
, полученной при фиксировании аргументов 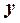 и
и 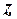 :
: 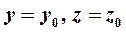 .
.
7. Скалярным полем 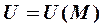 называется скалярная функция точки
называется скалярная функция точки 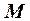 вместе с областью ее определения.
вместе с областью ее определения.
Уравнение
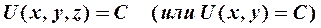 | (5) |
определяет семейство поверхностей (или линий) уровня, на которых скалярное поле принимает одно и то же значение 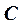 .
.
Скалярное поле 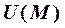 характеризуется градиентом
характеризуется градиентом
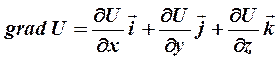 | (6) |
и производной по направлению 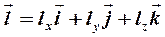 , равной скалярному произведению
, равной скалярному произведению 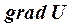 и единичного вектора
и единичного вектора 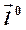 направления
направления 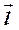 :
:
Пример 1. Составить уравнение касательной к нормали к кривой 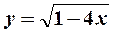 в точке, абсцисса которой
в точке, абсцисса которой  .
.
Решение. Найдем ординату точки касания: 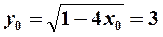 . Угловой коэффициент касательной равен значению производной в точке
. Угловой коэффициент касательной равен значению производной в точке 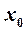 :
:
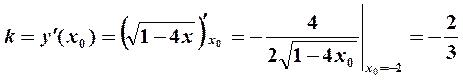 .
.
Подставляя значения 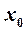 ,
, 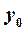 и
и 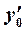 в уравнения касательной
в уравнения касательной 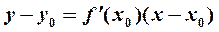 и нормали
и нормали 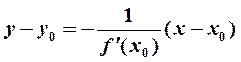 ,получаем:
,получаем:
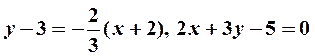 (касательная);
(касательная);
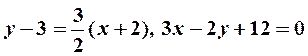 (нормаль).
(нормаль).
Пример 2. Используя правило Лопиталя, вычислить предел функции:
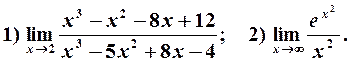
Решение. 1) Подстановка предельного значення аргумента 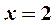 приводит к неопределенности вида
приводит к неопределенности вида 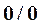 . Раскроем ее с помощью правила Лопиталя (1):
. Раскроем ее с помощью правила Лопиталя (1):
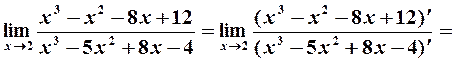
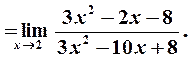
Однократное применение правила Лопиталя не приводит к раскрытию неопределенности (по-прежнему получаем 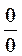 ), поэтому применим его еще раз:
), поэтому применим его еще раз:
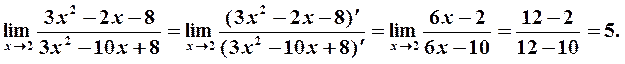
Таким образом, в результате двукратного применения правила Лопиталя находим, что искомый предел равен 5.
2) Убедившись, что имеет место неопределенность вида 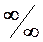 , применим правило Лопиталя:
, применим правило Лопиталя:
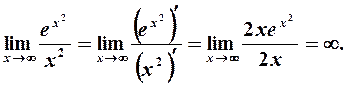
Пример 3. Исследовать на экстремум функцию 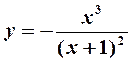 .
.
Решение. Находим первую производную: 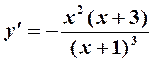 . Из уравнений
. Из уравнений 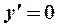 и
и 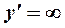 получаем точки, «подозрительные» на экстремум:
получаем точки, «подозрительные» на экстремум: 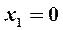 ,
, 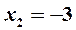 ,
, 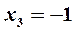 . Исследуем их, определяя знак первой производной слева и справа от каждой точки. Для наглядности результаты представим в виде таблицы изменения знака
. Исследуем их, определяя знак первой производной слева и справа от каждой точки. Для наглядности результаты представим в виде таблицы изменения знака 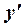 :
:
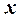 | 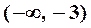 | 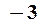 | 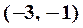 | 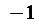 | 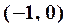 | 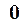 | 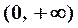 |
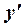 |  | 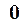 | 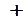 | 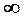 |  | 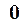 |  |
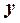 | убыв. | min | возр. | не опр. | убыв. | 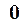 | убыв. |
В первой строке указаны интервалы, на которые область определения функции разбивается точками 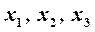 и сами эти точки. Во второй строке указаны знаки производной
и сами эти точки. Во второй строке указаны знаки производной 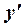 в интервалах монотонности. В третьей строке приведено заключение о поведении функции.
в интервалах монотонности. В третьей строке приведено заключение о поведении функции.
Исследуемая функция, как следует из таблицы, имеет минимум в точке 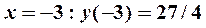 . Точки
. Точки 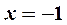 и
и 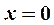 не являются точками экстремума, так как в первой точке функция не определена, а в окрестности второй точки первая производная сохраняет знак.
не являются точками экстремума, так как в первой точке функция не определена, а в окрестности второй точки первая производная сохраняет знак.
Пример 4. Найти асимптоты графика функции 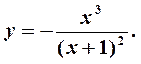
Решение. Точка 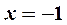 является точкой разрыва функции. Так как
является точкой разрыва функции. Так как 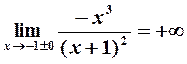 , то прямая
, то прямая 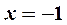 служит вертикальной ассимптотой графика функции [см. формулы (3)].
служит вертикальной ассимптотой графика функции [см. формулы (3)].
Ищем наклонные асимптоты 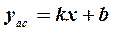 , используя формулы (2):
, используя формулы (2):
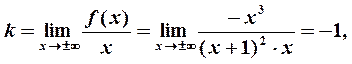
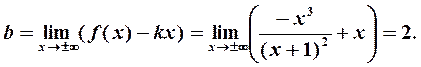
Таким образом, уравнение наклонной асимптоты имеет вид 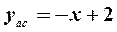 .
.
Пример 5. Построить график функции 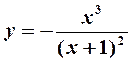 , используя общуюсхему исследования функции.
, используя общуюсхему исследования функции.
Решение. I. Область определения: 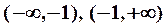 . Функция не является симметричной и периодической. Находим предельные значения функции:
. Функция не является симметричной и периодической. Находим предельные значения функции:
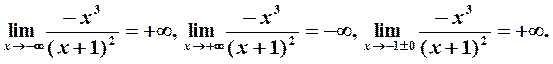
График функции имеет одну вертикальную асимптоту 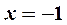 и одну наклонную асимптоту
и одну наклонную асимптоту 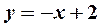 (см. пример 4). Он пересекает координатные оси в точке (0; 0).
(см. пример 4). Он пересекает координатные оси в точке (0; 0).
II. Функция имеет один минимум при 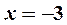 (см. пример 3).
(см. пример 3).
III. Вторая производная 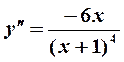 обращается в бесконечность при
обращается в бесконечность при 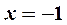 и равна нулю в точке
и равна нулю в точке 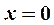 , которая является единственной точкой перегиба (см. таблицу):
, которая является единственной точкой перегиба (см. таблицу):
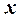 | 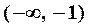 | 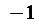 | 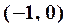 | 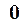 | 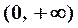 |
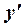 | 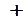 | 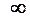 |  |  |  |
 | 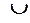 | не опр. | 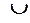 | точка перегиба | 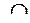 |
Учитывая полученные результаты, строим график функции 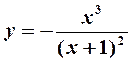 (рис. 9).
(рис. 9).
Пример 6. Найти первую производную функции 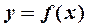 , заданной параметрически:
, заданной параметрически:
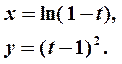
Решение. Дифференцируем 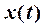 и
и 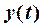 no параметру
no параметру 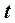 :
: 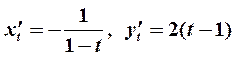 . Искомая производная от
. Искомая производная от 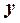 по
по 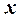 равна отношению производных от
равна отношению производных от 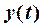 и от
и от 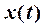 по
по 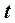 :
:
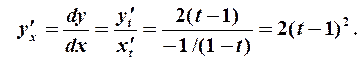
Пример 7. Найти частные производные 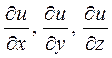 функции
функции 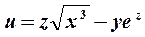 .
.
 Решение. Считая функцию
Решение. Считая функцию 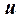 функцией только одной переменной
функцией только одной переменной 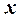 , а переменные
, а переменные 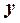 и
и 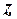 рассматривая как постоянные [см. формулу (4)], находим
рассматривая как постоянные [см. формулу (4)], находим 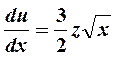 . Аналогично, считая
. Аналогично, считая 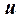 функцией только
функцией только 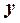 , а затем только
, а затем только 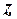 , получаем
, получаем 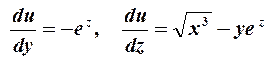 .
.
|
V ПЕРЕЧЕНЬ ЗАДАНИЙ ПО ВАРИАНТАМ
1. По координатам вершин пирамиды А1А2А3А4 найти: 1) длины ребер А1А2 и А1А3;2) угол между ребрами А1А2 и А1А3;3) площадь грани А1А2А3;4) объем пирамиды; 5) уравнения прямых А1А2 и А1А3;6) уравнения плоскостей А1А2А3 и А1А2А4;7) угол между плоскостями А1А2А3 и А1А2А4.
1. А1(-1; 2; 1), А2(-2; 2; 5), А3(-3; 3; 1), А4(-1; 4; 3).
2. А1(-2; I; -1), А2(-3; 1; 3), А3(-4; 2; -1), А4(-2; 3; 1).
3. А1(1; 1; 2), А2(0; 1; 6), А3(-l; 2; 2), A4(l; 3; 4).
4. А1(-1; -2; 1), А2(-2; -2; 5), А3(-3, -1; 1), A4(-1; 0; 3).
5. А1(2; -1; 1), А2(1; -1; 5), (0; 0; 1), (2; 1; 3).
6. А1(-l; 1; -2), А2(-2; 1; +2), А3(-3; 2; -2), А4(-1; 3;0).
7. А1 (1; 2; 1), А2(0; 2; 5), А3(-1;3; 1), А4(1; 4; 3).
8. А1(-2; -1; 1), А2(-3; -1; 5), А3(-4; 0; 1), А4(-2;1; 3).
9. А1 (1; -1; 2), А2(0; -1; 6), А3(-1; 0; 2), А4(1; 1; 4).
10. А1(1; -2; 1), А2(0; -2; 5), А3(-1; -1; 1), А4(0; 0; 3).
11. А1 (0; 3; 2), А2(-1; 3; 6), А3(-2; 4; 2), А4(0; 5; 4).


