Кусочно-кубические сплайны
Определение:Функция S(x) называется кубическим сплайном, если существует N кубических полиномов Sk(x) с коэффициентами sk,0, sk,1, sk,2, sk,3, которые удовлетворяют следующим условиям:
1. 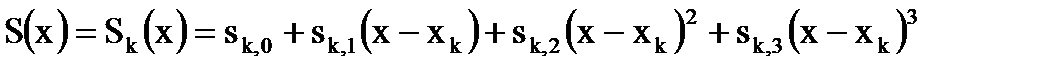 , для
, для 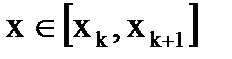
и 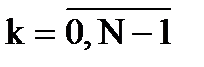 , т.е. кубический сплайн состоит из кубических полиномов.
, т.е. кубический сплайн состоит из кубических полиномов.
2. Кусочно-кубическое интерполирование задается совокупностью точек, т.е. 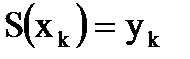 для
для 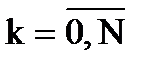 .
.
3. Кусочно-кубическое представление состояло из кривых, которые являются гладкими непрерывными функциями. Вторая и первая производные должны быть непрерывны: 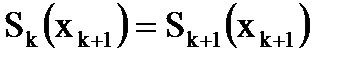 ,
, 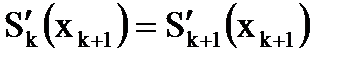 ,
, 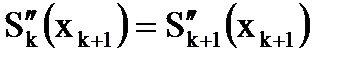 .
.
Наиболее часто на практике используется кубический сплайн следующего вида: 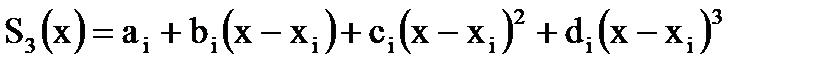 .
.
Для задания сплайна коэффициенты 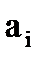 ,
, 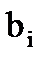 ,
, 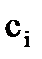 ,
, 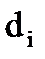 - подбираются так, чтобы
- подбираются так, чтобы 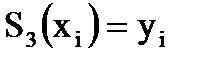 , а первая и вторая производные были непрерывными.
, а первая и вторая производные были непрерывными.
Леммы о сплайнах:
- Смыкающий (чертежный) сплайн.Существует единственный кубический сплайн, который имеет первую производную с граничными условиями
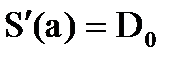 ,
, 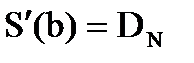 , т.е. смыкающий сплайн имеет определенный наклон в крайних точках.
, т.е. смыкающий сплайн имеет определенный наклон в крайних точках. - Естественный сплайн.Существует единственный кубический сплайн со свободными граничными условиями
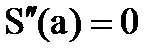 ,
, 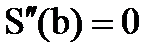 , т.е. сплайн допускает свободный наклон на краях для обеспечения положения, которое минимизирует осцилляцию кривой.
, т.е. сплайн допускает свободный наклон на краях для обеспечения положения, которое минимизирует осцилляцию кривой. - Экстраполяционный сплайн. Существует единственный кубический сплайн, который используется для экстраполирования по внутренним узлам, чтобы определить
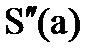 по узлам х1, х2 и
по узлам х1, х2 и 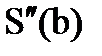 по узлам хN-1, хN-2.
по узлам хN-1, хN-2. - Сплайн, заканчивающийся параболой. Существует единственный кубический сплайн такой, что
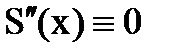 на интервале [x0, x1] и
на интервале [x0, x1] и 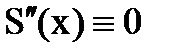 на интервале [xN-1, xN].
на интервале [xN-1, xN]. - Сплайн с заданной кривизной в крайних точках.Существует единственный кубический сплайн с заданными значениями второй производной в крайних точках.
Список литературы
1. Фадеев Д.К., Фадеева В.Н. Вычислительные методы линейной алгебры. - М.: ГИФМЛ, 1960, - 656 с.
2. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 2006, - 664 с.
3. Марчук Г.И. Методы вычислительной математики. - М.: Наука, 1980, - 536 с.
4. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. - М.: Наука, 1987, - 600 с.
5. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. - М.: Наука, 1989, - 656 с.
6. Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989, - 432 с.
7. Вержбицкий В.М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения): Учебное пособие для вузов. – М.: Высшая школа, 2001, - 382с.
[1] Например, F(a)<0 и F(b)>0.
[2] На анализируемом отрезке [a,b].
[3] Т.е. корни уравнений совпадают.
[4] Однократное выполнение процесса вычисления очередного приближения 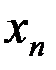 называется итерацией.
называется итерацией.
[5] Буквально - формулами вычисления площадей.
[6] Говорят, что формулы прямоугольников и трапеций имеют второй класс точности.
[7] Иначе говоря, параболой.
[8] Выведите данную формулу самостоятельно. Подсказка - примените формулу погрешности метода Симпсона.
[9] Для первой и последней точки разбиения значение функции умножать на коэффициент не надо.
[10] Если в программе вычисляется только один интеграл, то это не имеет значения. Но в некоторых профессиональных программах требуется вычислить интегралы для тысяч функций. В этом случае скорость метода имеет существенное значение.
[11] Интегралы от степенной функции легко подсчитать по формуле Ньютона - Лейбница.
