Интегралы от основных элементарных функций
Ранее мы получили основные производные элементарных функций. Приводимые ниже неопределенные интегралы представляют собой вычислительный аппарат интегрального исчисления. Часть формул непосредственно следует из определения интегрирования как операции, обратной дифференцированию. Справедливость всех формул легко проверить дифференцированием.
1) 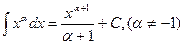 2) 2) 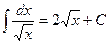 3) 3)  4) 4) 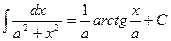 5) 5)  6) 6)  7) 7)  8) 8) 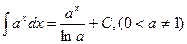 9) 9)  10) 10) 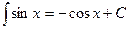 11) 11) 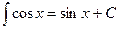 12) 12)  13) 13) 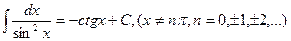 14) 14) 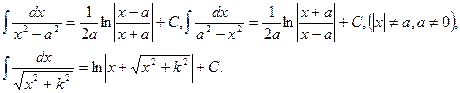 | (7.3.1) |
Приведенные выше интегралы принято называть табличными. Как было установлено ранее, операция дифференцирования не выводит функцию из класса элементарных. С операцией интегрирования дело обстоит иначе: интегралы от некоторых элементарных функций уже не являются элементарными функциями. Например:
 – интеграл Пуассона.
– интеграл Пуассона.
 или
или  – интеграл Френеля.
– интеграл Френеля.
 – интегральный синус.
– интегральный синус.
 – интегральный косинус.
– интегральный косинус.
Каждый из этих интегралов есть функция, которая не является элементарной. Они играют большую роль в прикладных науках. Например, интеграл Пуассона является одним из основных в теории вероятностей и статистике.
Отметим несколько полезных правил для вычисления интегралов.
Если известна первообразная функции 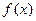 , т.е.
, т.е. 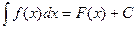 , а числа a и b константы, то:
, а числа a и b константы, то:
1. 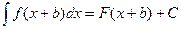 . 2. . 2.  . 3. . 3. 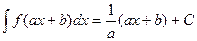 . . | (7.3.2) |
Пример
Вычислим интегралы.
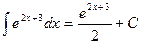 ,
,
 ,
,
 ,
,
 .
.
Методы интегрирования. Метод замены переменной
Замена переменной интегрирования является одним из самых эффективных приемов сведения неопределенных интегралов к табличным. Такой прием называется методом подстановки, или методом замены переменной. Он основан на следующей теореме.
Теорема
Пусть функция  определена на множестве Х, а функция
определена на множестве Х, а функция 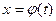 определена и дифференцируема на некотором промежутке Т. Таким образом, множество Х – множество значений функции
определена и дифференцируема на некотором промежутке Т. Таким образом, множество Х – множество значений функции 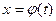 . Тогда, если функция
. Тогда, если функция  имеет первообразную на множестве Х, то на множестве Т справедлива формула
имеет первообразную на множестве Х, то на множестве Т справедлива формула
 | (7.4.1) |
Выражение (7.4.1) называется формулой замены переменной в неопределенном интеграле.
Рассмотрим применение этого приема на примерах.
1. . 
2. 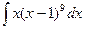 . Введем новую переменную
. Введем новую переменную  , тогда
, тогда 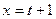 ,
, 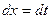 . Исходный интеграл преобразуется следующим образом:
. Исходный интеграл преобразуется следующим образом:
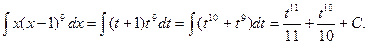
Возвращаясь к старой переменной, получим:
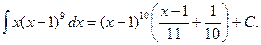
3.  .
.
4. 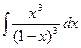 . Положим
. Положим  . Тогда
. Тогда  ,
,  . Отсюда по формуле (7.4.1) получаем
. Отсюда по формуле (7.4.1) получаем

 .
.
5.  .
.
6. 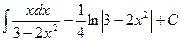 .
.
7. 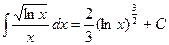 .
.
8. 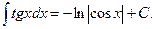
9.  . Здесь необходима следующая замена:
. Здесь необходима следующая замена:  . Тогда
. Тогда 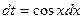 .
.
 .
.
Удачная замена переменной позволяет упростить исходный интеграл, а в простейших случаях свести его к табличному. Отметим, что новую переменную можно не выписывать явно (в таких случаях говорят о преобразовании функции под знаком дифференциала или о введении постоянных или переменных под знак дифференциала).
