Теорема Кронекера-Капелли

I Понятие ранга матрицы.

Рассмотрим произвольную матрицу А=(а_ij), i=1,2,…,m; j=1,2,…,n.

Минором k-го порядка матрицы А называют определитель k-го порядка с элементами, лежащими на пересечении любых k строк и любых k столбцов матрицы А (конечно, k≤min(m,n)).

Предположим, что хотя бы один из элементов a_ij матрицы А отличен от нуля. Тогда найдется такое натуральное число r, что будут выполнены два условия: 1) у матрицы А имеется минор r-го порядка, отличной от нуля; 2) всякий минор (r+1)-го порядка и более высокого (если таковые существуют), равен нулю.

Число r, удовлетворяющее требованиям 1) и 2), называют рангом матрицы А. Тот минор r-го порядка, который отличен от 0, называют базисным минором (конечно, у матрицы может быть несколько миноров r-го порядка, отличных от нуля). Строки и столбцы, на пересечении которых стоит базисный минор, называют базисными строками и базисными столбцами.

Смысл понятия ранга матрицы проясняет следующее утверждение, которое называют теоремой о базисном миноре:

базисные строки (базисные столбцы) линейно независимы; любая другая строка (столбец) является линейной комбинацией базисных строк (столбцов).

В связи с этой теоремой рангом матрицы называют также максимальное число линейно независимых столбцов (строк) матрицы.

II Критерий совместности системы линейных уравнений

Рассмотрим систему линейных уравнений

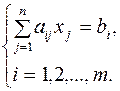(1)

Наряду с основной матрицей системы А=(а_ij) рассмотрим еще и так называемую расширенную матрицу А₁, полученную присоединением к А столбца свободных членов:

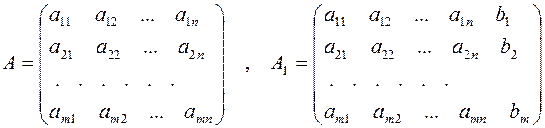
Вопрос о совместности системы полностью решается следующей теоремой.

Теорема Кронекера-Капелли. Система линейных уравнений (1) совместна тогда и только тогда, когда ранг расширенной матрицы этой системы равен рангу её основной матрицы.

Эта теорема только утверждает существование, но не дает, однако, никакого способа для практического разыскания всех решений системы.