Свойства преобразования Лапласа
ГЛАВА 4
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Определение интеграла от функции комплексного
Переменного и его свойства
Определение интеграла
Пусть задана некоторая ориентированная непрерывная кривая 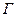 и на ней однозначная функция комплексного переменного
и на ней однозначная функция комплексного переменного 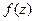 . Разобьем кривую
. Разобьем кривую 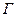 произвольно на
произвольно на 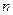 элементарных дуг точками
элементарных дуг точками 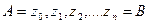 , записанными в порядке их следования на кривой (точки
, записанными в порядке их следования на кривой (точки 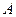 и
и 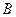 - начало и конец кривой
- начало и конец кривой 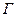 соответственно), и на каждой из дуг
соответственно), и на каждой из дуг 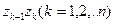 также произвольно возьмем по точке
также произвольно возьмем по точке 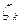 . (См. рис. (4.1)). Обозначим
. (См. рис. (4.1)). Обозначим 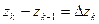 .
.
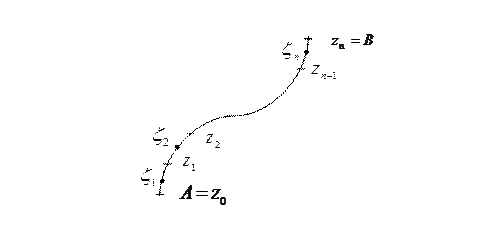
Рис. 4.1
Назовем интегралом  вдоль
вдоль  предел
предел
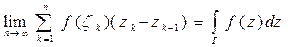 , (4.1)
, (4.1)
если он существует и не зависит ни от способа разбиения кривой  , ни от выбора точек
, ни от выбора точек 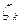 .
.
Вопрос о существовании комплексного интеграла (4.1) сводится к вопросу о существовании криволинейного действительного интеграла.
Действительно, положив 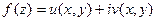 ,
,
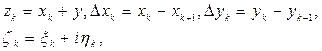
получим 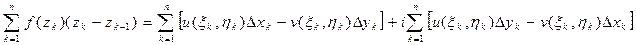 . Замечаем, что суммы в правой части полученного равенства представляют собой интегральные суммы криволинейных интегралов
. Замечаем, что суммы в правой части полученного равенства представляют собой интегральные суммы криволинейных интегралов 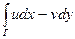 и
и 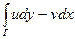 соответственно. А поэтому, как следует из теоремы о существовании криволинейного интеграла, для существования интеграла (4.1) достаточно, чтобы кривая
соответственно. А поэтому, как следует из теоремы о существовании криволинейного интеграла, для существования интеграла (4.1) достаточно, чтобы кривая 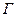 была кусочно-гладкой, а функции
была кусочно-гладкой, а функции  и
и 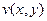 кусочно-непрерывными функциями действительных переменных, или что-то же самое, чтобы функция
кусочно-непрерывными функциями действительных переменных, или что-то же самое, чтобы функция 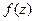 была непрерывной на
была непрерывной на  . Итак, интеграл (4.1) можно связать с криволинейными интегралами формулой
. Итак, интеграл (4.1) можно связать с криволинейными интегралами формулой
 . (4.2)
. (4.2)
Примеры:
1. Пусть  . Тогда интегральная сумма
. Тогда интегральная сумма
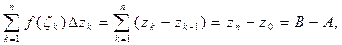
следовательно,
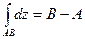 .
.
В частности, если 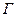 - замкнутая кривая
- замкнутая кривая 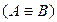 , то
, то
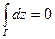 .
.
2. Пусть 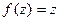 ,тогда, полагая
,тогда, полагая  , получим интегральные суммы
, получим интегральные суммы 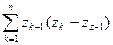 , если же положить
, если же положить 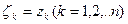 , то интегральные суммы примут вид
, то интегральные суммы примут вид 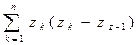 .
.
Так как эти суммы имеют один и тот же предел, то их среднее арифметическое имеет тот же предел 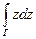 , следовательно
, следовательно

Свойства интеграла функции комплексного переменного
1.  . (4.3)
. (4.3)
2. 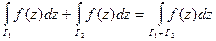 , (4.4)
, (4.4)
где  обозначает кривую, составленную из дуг
обозначает кривую, составленную из дуг  и
и 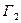 ,так что конец
,так что конец  совпадает с началом
совпадает с началом 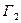 .
.
3. 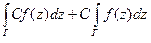 , (4.5)
, (4.5)
где 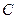 - комплексная постоянная.
- комплексная постоянная.
4. 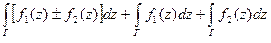 . (4.6)
. (4.6)
Свойства 1-4 могут быть получены из определения интеграла или из формулы (4.2)
5. 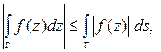 (4.7)
(4.7)
где 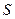 - длина кривой
- длина кривой 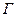 , отсчитываемая от начала до произвольной ее точки.
, отсчитываемая от начала до произвольной ее точки.
Интеграл  часто записывают также как
часто записывают также как 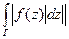 . Действительно, в силу неравенства
. Действительно, в силу неравенства
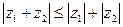
для модуля интегральной суммы можно записать:
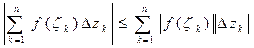 ,
,
но  длины
длины  , следовательно,
, следовательно,
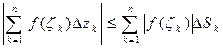 .
.
Переходя к пределу в последнем неравенстве при условии  , получаем формулу (4.7). В частности, если
, получаем формулу (4.7). В частности, если 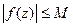 для
для  , из формулы (4.7) следует
, из формулы (4.7) следует 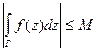 для
для  .
.
6. Пусть  - действительный параметр) – уравнение гладкой кривой
- действительный параметр) – уравнение гладкой кривой 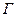 , тогда
, тогда
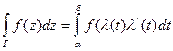 . (4.8)
. (4.8)
Действительно, на основании формулы (4.4) способ вычисления криволинейного интеграла дает

Пример.
Вычислить интеграл 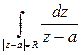 , причем окружность проходится против часовой стрелки. Уравнение окружности
, причем окружность проходится против часовой стрелки. Уравнение окружности 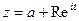 , где
, где 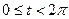 . Применяя формулу (4.4) имеем
. Применяя формулу (4.4) имеем
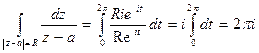 .
.
Замечание. Пусть 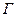 - замкнутая кусочно-гладкая кривая Жордана. Условимся под записью
- замкнутая кусочно-гладкая кривая Жордана. Условимся под записью 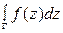 понимать интеграл вдоль контура Г в положительном направлении (т.е. когда область ограниченная кривой Г , остается слева при движении по Г). Когда интегрирование по контуру Г производится в отрицательном направлении, будем писать
понимать интеграл вдоль контура Г в положительном направлении (т.е. когда область ограниченная кривой Г , остается слева при движении по Г). Когда интегрирование по контуру Г производится в отрицательном направлении, будем писать 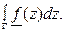
Теорема Коши
Теорема Коши.
Если функция f(z) аналитична в односвязной области D и Г - произвольная замкнутая кусочно-гладкая кривая Жордана в D, то
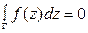 . (4.9)
. (4.9)
Мы докажем эту теорему при дополнительном предположении, что производная 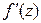 функции
функции  непрерывна в D.
непрерывна в D.
Пусть  тогда
тогда
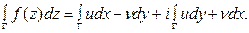
В силу предположения, функции u (х, у) и v(х, у) непрерывны в области D вместе со своими частными производными, а потому для них справедлива формула Грина:

где DГ – область, ограниченная контуром Г. Равенство нулю двойных интегралов следует из условий Коши-Римана, выполняющихся для аналитической в D функции f(z). А из полученных равенств получаем: 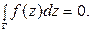 Теорема доказана.
Теорема доказана.
Теорема Коши доказана нами для односвязной области, но ее можно обобщить и на случай многосвязной области.
Теорема Коши (для многосвязной области)
Пусть f(z) - аналитическая в области D функция. И пусть 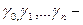 замкнутые кусочно-гладкие кривые Жордана, лежащие внутри области D, причем
замкнутые кусочно-гладкие кривые Жордана, лежащие внутри области D, причем 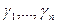 лежат внутри
лежат внутри 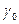 и во внешности друг друга, и многосвязная (n + 1 – связная) область G, ограниченная кривыми
и во внешности друг друга, и многосвязная (n + 1 – связная) область G, ограниченная кривыми 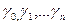 ,
, 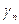 , лежит внутри области D.
, лежит внутри области D.
Обозначим через Г сложный контур, состоящий из контура 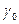 (проходимого в положительно направлении) и контуров
(проходимого в положительно направлении) и контуров 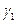 ,
,  ,
, 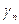 (проходимых в отрицательном направлении). (См. рис. 4.2)
(проходимых в отрицательном направлении). (См. рис. 4.2)
Рис. 4.2
Тогда справедлива формула: 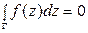 , где
, где

Это равенство можно переписать в такой форме:
Доказательство. Соединим последовательно контуры 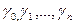 с помощью криволинейных отрезков, лежащих внутри D. Тогда вместо (n + 1)-го замкнутого контура, будем иметь два контура Г1 и Г2, ограничивающих соответственно две области D1 и D2. При этом
с помощью криволинейных отрезков, лежащих внутри D. Тогда вместо (n + 1)-го замкнутого контура, будем иметь два контура Г1 и Г2, ограничивающих соответственно две области D1 и D2. При этом 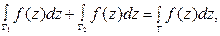 так как каждый вспомогательный отрезок, соединяющий
так как каждый вспомогательный отрезок, соединяющий 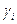 и
и  (i = 0, 1, …, n - 1), проходится дважды в разных направлениях. Каждая из областей D1 и D2, является односвязной и принадлежит вместе со своей границей области D.
(i = 0, 1, …, n - 1), проходится дважды в разных направлениях. Каждая из областей D1 и D2, является односвязной и принадлежит вместе со своей границей области D.
Поэтому для каждой из них справедлива теорема Коши для односвязной области:
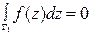 ;
; 
следовательно,
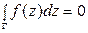 ,
,
что и требовалось доказать.
Пример.
Вычислить интеграл 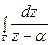 по замкнутому контуру Г.
по замкнутому контуру Г.
1. Пусть точка z = а не принадлежит области, ограниченной Г, тогда по
теореме Коши 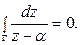
2. Предположим, что точка z = а принадлежит области ограниченной
контуром Г. (См. рис. 4.3).
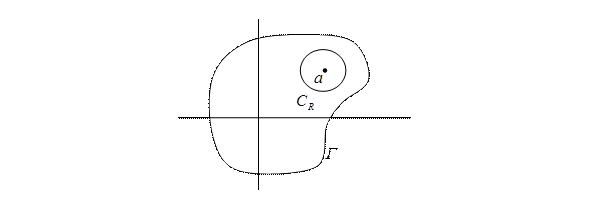
Рис. 4.3
В этом случае теорема Коши не применима. Возьмем в качестве нового контура окружность CR достаточно малого радиуса R с центром в точке a такую, чтобы она лежала внутри контура Г.
Так как в двухсвязной области, ограниченной CR и Г, применима теорема Коши, то

или
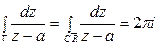
(последний интеграл вычислен в примере §1).
Замечание.Из теоремы Коши следует, что интеграл от функции f(z), аналитической в односвязной области D, не зависит от пути интегрирования, а зависит лишь от его начала и конца, т.е.  , где А и В – соответственно начало и конец кривой, принадлежащей области D аналитичности функции f (z).
, где А и В – соответственно начало и конец кривой, принадлежащей области D аналитичности функции f (z).
Неопределенный интеграл
В интеграле 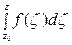 зафиксируем нижний придел z0 интегрирования и будем рассматривать интеграл как функцию верхнего предела
зафиксируем нижний придел z0 интегрирования и будем рассматривать интеграл как функцию верхнего предела 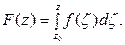 Тогда для функции f (z) можно доказать теорему.
Тогда для функции f (z) можно доказать теорему.
Теорема.
Если функция f (z) непрерывна в односвязной области D и интеграл
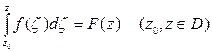 (4.10)
(4.10)
не зависит от пути интегрирования, то однозначная в области D функция f (z) аналитична в D, причем 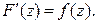
Доказательство. По определению производной и на основании свойств интеграла можем записать

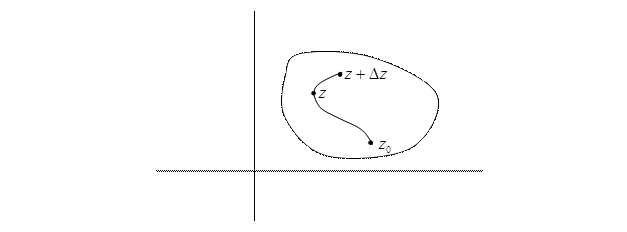
Рис. 4.4
где z – произвольная точка D, 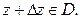 (рис. 4.4). В силу непрерывности функции f(z)
(рис. 4.4). В силу непрерывности функции f(z)
в точке z имеем
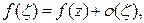
где 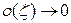 при
при 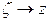 .
.
Учитывая это, получим:
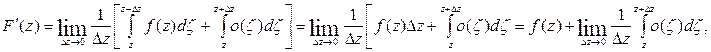
но
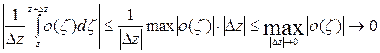 при
при  .
.
(путь интегрирования от точки z до точки 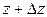 считаем прямолинейным).
считаем прямолинейным).
Отсюда  и, следовательно,
и, следовательно,
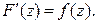
Функция Ф(z) называется первообразной для функции f(z) в некоторой области D, если (Ф(z))′=  для
для 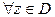 .
.
Из доказанной теоремы следует, что  является первообразной для функции f(z). Можно легко доказать следующую теорему.
является первообразной для функции f(z). Можно легко доказать следующую теорему.
Теорема.
Любые две первообразные одной и той же функции отличаются друг от друга не более, чем на постоянное слагаемое.
Доказательство предоставляется провести самостоятельно.
На основании этой теоремы можно записать:
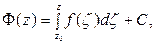 где Ф(z) – любая первообразная функция
где Ф(z) – любая первообразная функция 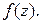
При  следовательно,
следовательно,
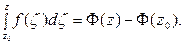 (4.11)
(4.11)
Мы получили формулу, аналогичную формуле Ньютона-Лейбница для вычисления определенного интеграла функции действительного переменного.
Пример.
Рассмотрим  . Подынтегральная функция аналитична в любой односвязной области D комплексной плоскости, не содержащей току z = 0, например, в области
. Подынтегральная функция аналитична в любой односвязной области D комплексной плоскости, не содержащей току z = 0, например, в области  . В этой области
. В этой области  является первообразной для функции
является первообразной для функции 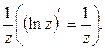 Поэтому
Поэтому 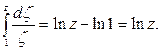 Предположим теперь, что линия, соединяющая точку z = 1 с точкой z, пересекает отрицательную
Предположим теперь, что линия, соединяющая точку z = 1 с точкой z, пересекает отрицательную

Рис.4.5 Рис.4.6
действительную ось (рис. 4.5). В этом случае, учитывая пример 1 § 1, будем иметь
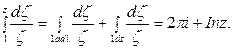
Если путь интегрирования совершает k оборотов вокруг точки z = 0, то 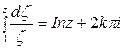 (знак определяется направлением движения по кривой). Таким образом, мы получаем ту или иную ветвь многозначной функции Lnz . Можно написать
(знак определяется направлением движения по кривой). Таким образом, мы получаем ту или иную ветвь многозначной функции Lnz . Можно написать  .
.
§ 4. Интегральная формула Коши и ее приложения.
Интегральная формула Коши.
Пусть Г кусочно-гладкая граница односвязной области D и f(z) – функция, аналитическая в области D и непрерывная в замкнутой области 
Рассмотрим произвольную точку 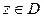 :
:
Функция переменной  аналитична всюду в области D за исключением точки
аналитична всюду в области D за исключением точки 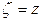 .
.
Опишем окружность 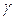 радиуса р с центром в точке z, принадлежащую области D (рис. 4.6).
радиуса р с центром в точке z, принадлежащую области D (рис. 4.6).
Так как функция f(z) аналитична в двухсвязной области ограниченной Г и 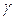 , и непрерывна на ее границе
, и непрерывна на ее границе 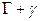 , то по теореме Коши
, то по теореме Коши  , т.е. интеграл
, т.е. интеграл 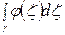 не зависит от радиуса р окружности. Так как существует
не зависит от радиуса р окружности. Так как существует 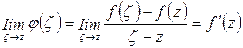 , то доопределив функцию
, то доопределив функцию 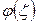 в точке
в точке 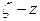 , положив
, положив 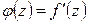 , будем иметь функцию
, будем иметь функцию 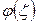 , непрерывную в области D, а значит и ограниченную в ней:
, непрерывную в области D, а значит и ограниченную в ней:  .
.
Учитывая это, получим:
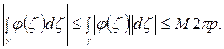
В силу произвольности р и постоянства M
 т.е.
т.е. 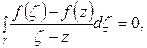 или
или

отсюда получаем интегральную формулу Коши:

т.е. значение функции f(z), аналитической в области D непрерывна в 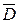 , можно выразить чрез ее значения на границе области Г.
, можно выразить чрез ее значения на границе области Г.
Пример 1.Вычислить интеграл 
Т. к. 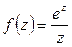 аналитична в замкнутой области, ограниченной окружностью
аналитична в замкнутой области, ограниченной окружностью 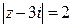 , то по интегральной формуле Коши имеем:
, то по интегральной формуле Коши имеем:

Если рассмотреть этот же интеграл, но в качестве контура взять
окружность 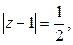 то
то 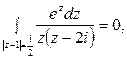
т. к. подынтегральная функция аналитична всюду в замкнутой области, ограниченной окружностью 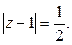
Правую часть интегральной формулы Коши 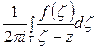 называют интегралом Коши.
называют интегралом Коши.
Следствие 1. В частном случае, если кривая Г является окружностью с центром в точке z радиуса R, т. е. 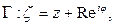 мы имеем
мы имеем  и тогда
и тогда

т. е. f (z) есть среднее арифметическое значение f ( 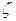 ) на окружности центром z.
) на окружности центром z.
Интегральная формула Коши справедлива и для многосвязной области. Действительно, пусть D многосвязная область, ограниченная контуром 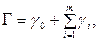 и функция f (z) аналитична в D и непрерывна
и функция f (z) аналитична в D и непрерывна 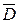 .
.

Рис. 4.7.
Рассмотрим произвольную точку 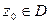 . Окружим точку z окружностью CR, так, чтобы область, ограниченная окружностью CR , вместе с самой окружностью полностью принадлежала D (рис. 4.7). Тогда функция
. Окружим точку z окружностью CR, так, чтобы область, ограниченная окружностью CR , вместе с самой окружностью полностью принадлежала D (рис. 4.7). Тогда функция 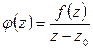 удовлетворяет условиям теоремы Коши в (m + 2)-связной области ограниченной контуром
удовлетворяет условиям теоремы Коши в (m + 2)-связной области ограниченной контуром 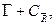 и следовательно,
и следовательно,
 или
или 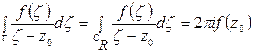
на основании доказанной выше теоремы.
Отсюда 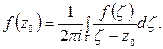
Неограниченная дифференцируемость аналитической
функции
Используя представление функции интегралом Коши (6.6), можно показать, что аналитическая в области в функция дифференцируема в точках области D сколько угодно раз.
Теорема. Если функция f (z) аналитична в области D и непрерывна в области 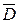 , то она обладает в области D производными всех порядков, причем n-ая производная представляется формулой
, то она обладает в области D производными всех порядков, причем n-ая производная представляется формулой
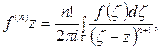 (6.7)
(6.7)
где Г - граница области D.
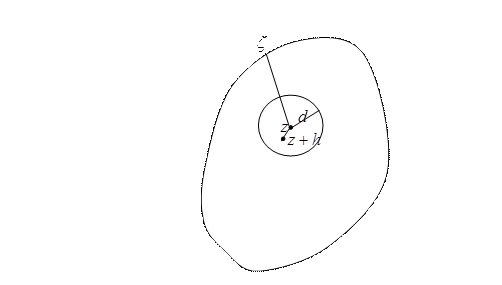
Рис. 4.8
Доказательство. Пусть z – произвольная точка области D (Pис.4.8). На основании интегральной формулы Коши имеем 

Оценим разность
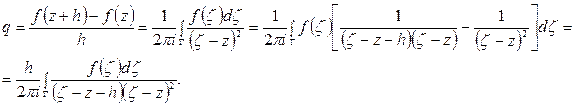
Из непрерывности f (z) на замкнутом множестве Г следует ограниченность f (z) на Г, т.е. существует М >0 такое, что 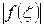 < М для
< М для  С другой стороны
С другой стороны  поэтому существует
поэтому существует  такое, что
такое, что 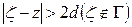 . Тогда для
. Тогда для  имеем
имеем 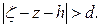
Отсюда
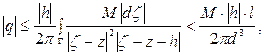
Где l - длина Г. Т. к. M, l, d не зависят от L, то при 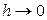
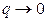 . Следовательно,
. Следовательно,
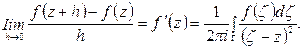
Мы доказали формулу (6.7) для n = 1.
Для любого n > 1 формула доказывается индукцией по n.
Пример 2. Вычислить 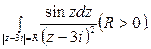 К этому интегралу можно применить формулу (6.7), тогда
К этому интегралу можно применить формулу (6.7), тогда

Замечание: неравенства Коши.
Обозначим через М максимум 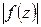 в области D, через R расстояние от точки z до границы и через l длину границы Г, тогда из интегральной формулы для n-ой производной имеем:
в области D, через R расстояние от точки z до границы и через l длину границы Г, тогда из интегральной формулы для n-ой производной имеем:
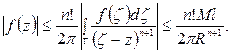
В частности, если (z) аналитична в круге 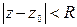 , то принимая в качестве D этот круг, будем иметь:
, то принимая в качестве D этот круг, будем иметь:
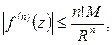 (n = 0, 1, 2…). (6.8)
(n = 0, 1, 2…). (6.8)
Эти неравенства называют неравенствами Коши.
Теорема Лиувилля
Если f (z) аналитична во всей плоскости и ограничена, то она постоянна.
Доказательство. Пусть 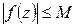 , тогда на основании неравенства Коши (6.3) для
, тогда на основании неравенства Коши (6.3) для 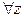 и
и 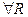 при п = 1 имеем
при п = 1 имеем 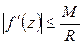 , но так как левая часть неравенства не зависит от R, а правая
, но так как левая часть неравенства не зависит от R, а правая 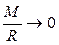 при
при  , то
, то 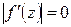 . Таким образом f (z) = 0 во всей плоскости.
. Таким образом f (z) = 0 во всей плоскости.
Используя формулу Лейбница (6.5), имеем
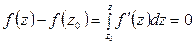 т. е.
т. е. 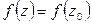 для
для 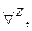
функция 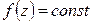 во всей комплексной плоскости.
во всей комплексной плоскости.
Отметим без доказательства еще две теоремы.
Обращение теоремы Коши (теорема Морера).
Если функция f (z), непрерывная в односвязной области D, для всякого кусочно-гладкого замкнутого контура Жордана Г, лежащего в области D, удовлетворяет равенству  , то f (z) аналитична в области.
, то f (z) аналитична в области.
Теорема (принцип максимума модуля).
Если функция f (z), не равная тождественно постоянной, аналитична в области D и непрерывная в 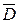 , то ее модуль не может достигать наибольшего значения во внутренней точке области D. (Аналогичное утверждение справедливо для минимума
, то ее модуль не может достигать наибольшего значения во внутренней точке области D. (Аналогичное утверждение справедливо для минимума 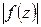 при дополнительном условии
при дополнительном условии 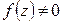 для
для 
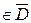 ).
).
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Современные расчеты разнообразных механических, электрических, гидравлических систем не могут выполняться без изучения переходных процессов в этих системах. Операционное исчисление является удобным аппаратом аналитического исследования различных неустановившихся процессов и находит широкое применение при решении многих задач нефтепромысловой механики.
Идея применения операционных методов заключается в том, что при решении задач искомая функция заменяется некоторым преобразованным выражением (изображением) действия над которым проще, чем над самой функцией (оригиналом). Решение задачи получается после нахождения изображения путем обратного перехода к оригиналу. Аналогией может служить идея применения логарифмов в элементарной математике, когда действию например, умножения чисел соответствует более простое действие сложения логарифмов этих чисел. Кроме того, применением операционного метода, как правило, исключается одно из переменных, что намного облегчает решение задачи.
Возможны случаи, когда применением операционного метода обыкновенное дифференциальное уравнение можно свести к алгебраическому.
Оригинал и изображение
В основе операционного исчисления лежит преобразование Лапласа.
Пусть имеется функция действительного переменного f (t), кусочно-непрерывная при 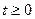 , равная нулю при
, равная нулю при 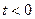 . Кроме того, будем считать, что существуют такие числа М >
. Кроме того, будем считать, что существуют такие числа М > 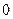 и
и 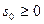 , что для всех t имеет место неравенство
, что для всех t имеет место неравенство
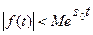
( s0 – показатель роста  ) т. е.
) т. е.  может возрастать с ростом t не быстрее чем
может возрастать с ростом t не быстрее чем  . Такую функцию
. Такую функцию  будем называть оригиналом. Перечисленным условиям удовлетворяют почти все функции с которыми приходится сталкиваться при изучении различных физических процессов. Функцию
будем называть оригиналом. Перечисленным условиям удовлетворяют почти все функции с которыми приходится сталкиваться при изучении различных физических процессов. Функцию 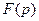 , определяемую равенством
, определяемую равенством
 (10.1)
(10.1)
где  - комплексная переменная, назовем изображением функции
- комплексная переменная, назовем изображением функции  .
.
Преобразование, сопоставляющее функции  изображение
изображение 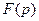 , называется преобразованием Лапласа. Тот факт, что
, называется преобразованием Лапласа. Тот факт, что 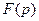 является изображением оригинала
является изображением оригинала 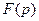 записывают так:
записывают так:
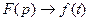 , или
, или  , или
, или 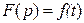 .
.
Пример. Найдем изображение функции
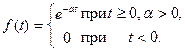
По определению преобразования Лапласа имеем

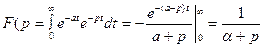 .
.
Следовательно, 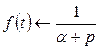 .
.
Пример. Если в предыдущем примере положить а=0, то получим изображение для функции, которая называется единичной функцией (функцией Хевисайда)
ơ (t) = ׃ 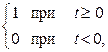

а именно ơ (t) 
Из определения изображения (10.1) видно, что для того, чтобы преобразование Лапласа было возможно, необходимо чтобы несобственный интеграл (10.1) существовал для некорой области значений р. Ответ на вопрос о существовании изображения дает теорема:
Для всякого оригинала  изображение F (р) определено в полуплоскости
изображение F (р) определено в полуплоскости 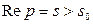 причем функция F (р) аналитична в этой полуплоскости.
причем функция F (р) аналитична в этой полуплоскости.
Доказательство. Пусть 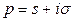 — любая точка полуплоскости
— любая точка полуплоскости  , тогда, пользуясь определением оригинала, имеем
, тогда, пользуясь определением оригинала, имеем
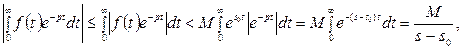 т. к.
т. к. 
(10.3)
Отсюда вытекает сходимость интеграла, т. е, факт существования изображения F(р) в полуплоскости  доказан. Доказательство аналитичности F(р) в полуплоскости
доказан. Доказательство аналитичности F(р) в полуплоскости  , т. е. существования производной
, т. е. существования производной 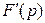 в любой точке этой полуплоскости, интересующийся читатель может найти в литературе [1].
в любой точке этой полуплоскости, интересующийся читатель может найти в литературе [1].
Отметим поведение изображения в бесконечно удаленной точке. Из неравенства (10.3) следует, что если 
 так, что при этом
так, что при этом  , то
, то 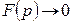 . Если, в частности, F(р) – аналитическая функция в бесконечно удаленной точке, то
. Если, в частности, F(р) – аналитическая функция в бесконечно удаленной точке, то 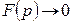 при
при  по любому закону, так как
по любому закону, так как 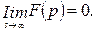 .
.
Итак,
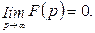
Сформулируем еще теорему единственности оригинала:
Если F(р) служит изображением двух оригиналов 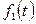 и
и 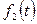 , то эти оригиналы совпадают друг с другом во всех точках, в которых они непрерывны.
, то эти оригиналы совпадают друг с другом во всех точках, в которых они непрерывны.
Свойства преобразования Лапласа
Теорема линейности.
Любой линейной комбинации оригиналов 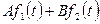 соответствует такая же линейная комбинация изображений. Доказательство. Исходя из определения изображения (10.1), имеем
соответствует такая же линейная комбинация изображений. Доказательство. Исходя из определения изображения (10.1), имеем
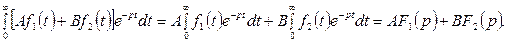
Пример 
Пример.Найдем изображения тригонометрических и гиперболических функций, применяя теорему линейности

Теорема подобия
Если  и число
и число 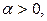 то
то

Доказательство. По определению (10.1)

В последнем интеграле сделаем замену переменной u = at, тогда
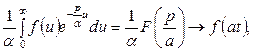
Пример. Так как 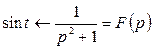 , то следовательно,
, то следовательно,
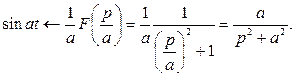
Теорема запаздывания
Если F (p) является изображением для оригинала f (t) и число t0>0, то функция
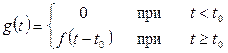

имеет изображение 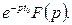
Функцию g (t) можно записать, пользуясь определением единичной функции, так
ơ (t)= ơ (t - t0) f (t - t0).
Графиком функции g (t) является график функции f (t), сдвинутый вправо на t0 вдоль оси t.
Доказательство.Опираясь на равенство (10.1), имеем
ơ (t - t0) f (t - t0) 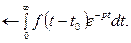
Обозначая t – t0 =  , получим
, получим
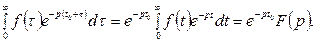
Пример. Найдем изображение функции
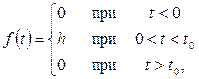
график который изображен на рисунке (10.1)
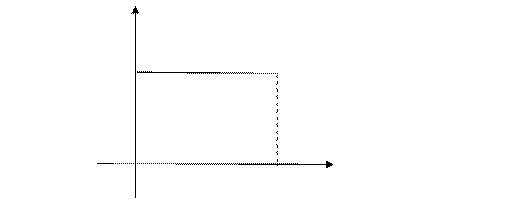
Рис. 10.1
С помощью единичной функции можно данную функцию записать в виде
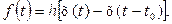
Тогда по теореме запаздывания и зная, что 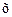 (t)
(t) 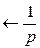 , будем иметь
, будем иметь
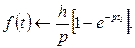
Теорема смещения
Если  и
и  - любое комплексное число, то
- любое комплексное число, то 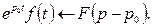
Доказательство. По определению преобразования Лапласа имеем
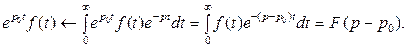
Причем изображение F (p - p0) определено при Re (p – p0)> s0 т. е. в полуплоскости
Re p > s0 +Re p0. Теорему смещения можно использовать для отыскания оригинала смещенного изображения F (p – p0), зная оригинал F (p).
Например, зная изображение для функции 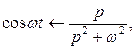 находим изображение для затухшей функции
находим изображение для затухшей функции

Аналогично, если
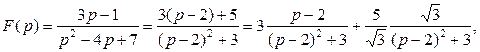
то 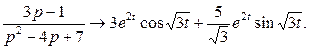
Теорема свертывания
Пусть f1 (t) 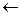 F (p) и f2 (t)
F (p) и f2 (t) 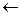 F2 (p). Функция
F2 (p). Функция 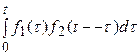 называется свертываемой функцией f1 (t) и f2 (t) и обозначается обычно так f1* f2. При этом имеет место следующая теорема:
называется свертываемой функцией f1 (t) и f2 (t) и обозначается обычно так f1* f2. При этом имеет место следующая теорема:
Оригинал, соответствующий произведению двух изображений. Равен свертке оригиналов сомножителей, т. е.
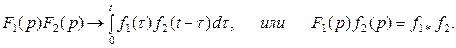
Доказательство. По определению преобразования Лапласа (10.1) имеем

В этом интеграле переменим порядок интегрирования (см. рис. 10.2).
Получим
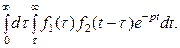
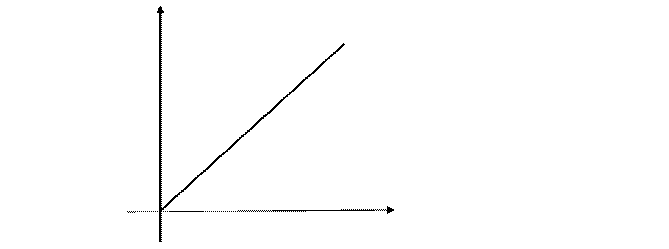
Рис. 10.2
Во внутреннем интеграле произведем подстановку 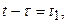 тогда получим
тогда получим
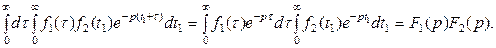
Пример.Найти оригинал по его изображению 
Так как  то на основании теоремы свертывания
то на основании теоремы свертывания
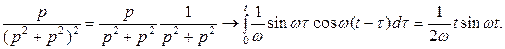
Теорема дифференцирования оригинала.
Если 
Доказательство. Преобразованием Лапласа для 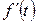 является интеграл
является интеграл

Интегрируя по частям, получим
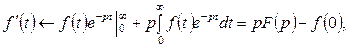 так как
так как 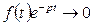 при
при 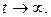
Последнее верно, потому что f (t) является оригиналом и, следовательно,

Последовательным применением этой теоремы можно получить изображения для производных высшего порядка:

Пример.Найти решение дифференциального уравнения
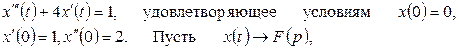
тогда 

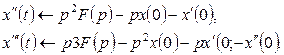
Уравнение в изображениях будет иметь вид

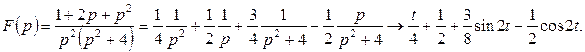
Итак, 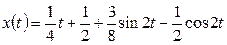 есть решение данного дифференциального уравнения.
есть решение данного дифференциального уравнения.
Следствия. Асимптотическое поведение изображения
1. Если f (t) оригинал, а F (p) аналитическая в бесконечности функция, то
 (10.6)
(10.6)
В самом деле, любое изображение, аналитическое в бесконечности, стремиться к нулю при  Поэтому изображение функции
Поэтому изображение функции 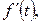 равное
равное 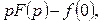 стремится к нулю при
стремится к нулю при 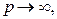 т. е.
т. е.  Откуда следует равенство (10.6).
Откуда следует равенство (10.6).
Пользуясь этим предельным соотношением, можно найти начальное значение оригинала 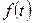 по его изображению
по его изображению  не вычисляя самого оригинала.
не вычисляя самого оригинала.
2. Если 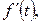 оригинал и существует предел
оригинал и существует предел 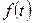 при
при 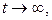 то
то
 (10.7)
(10.7)
Воспользуемся теоремой о дифференцировании оригинала

Перейдем к пределу при 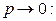
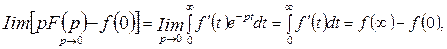
отсюда имеем
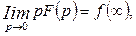
так как 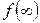 по предположению существует. (Возможность перехода к пределу под знаком интеграла можно обосновать.)
по предположению существует. (Возможность перехода к пределу под знаком интеграла можно обосновать.)
Теорема интегрирования оригинала.
Если 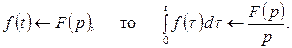
Доказательство. Пусть изображением  является функция Ф (p). Тогда по теореме дифференцирования оригинала будем иметь
является функция Ф (p). Тогда по теореме дифференцирования оригинала будем иметь
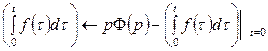 ,
,
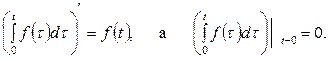
Следовательно, 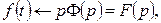 то есть
то есть

Итак,
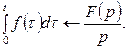
Пример.Найти оригинал по его изображению 
Так как  то
то

Теорема дифференцирования изображения
Если 
Доказательство. Пользуясь равенством (10.1) напишем

Продифференцируем по параметру p это выражение
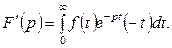
А это и означает, что 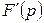 является изображением для
является изображением для 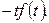
Пример.Зная, что 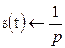 и применяя теорему дифференцирования изображения, получим
и применяя теорему дифференцирования изображения, получим
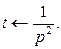
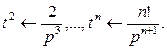
Теорема интегрирования изображения
Если  и
и 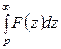 сходится, то
сходится, то 
Доказательство. Пусть изображением для  является функцией
является функцией 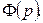 Тогда по теореме дифференцирования изображения
Тогда по теореме дифференцирования изображения 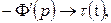 т. е.
т. е. 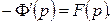
Интегрируя последнее равенство от p до q и переходя к пределу при 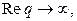 получим
получим
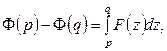
или же

Здесь мы воспользовались тем, что 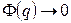 при
при 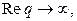 что следует из (10.3).
что следует из (10.3).
Пример.Найти изображение функции 
Так как  то
то

