Приближенное решение обыкновенных дифференциальных уравнений. Метод Эйлера

Практическое занятие №25

«Численное интегрирование с помощью формул прямоугольников, трапеций, Симпсона.

Приближенное решение дифференциальных уравнений с помощью формул Эйлера»

1. Цель: Выработать навыки и умения по применению методов приближённого

интегрирования – формул прямоугольников, трапеций и Симпсона, в решении

приближенными методами дифференциальных уравнений

Пояснения к работе

2.1 Краткие теоретические сведения:

Формула прямоугольников

Известно, что не для всякой непрерывной функции ее первообразная выражается через элементарные функции. Кроме того, на практике сталкиваются с необходимостью вычислять интегралы от функций, заданных табличным или графическим способами, а так же интегралы от функций, первообразные которых выражаются через элементарные очень сложно, что требует большой вычислительной работы и с практической точки зрения нерационально. В этих случаях вычисление определенного интеграла по формуле Ньютона – Лейбница затруднительно, поэтому прибегают к различным методам приближенного интегрирования. Наиболее простым методом приближенного вычисления определенного интеграла является метод прямоугольников, основанный на непосредственном определении интеграла:

,

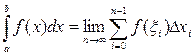где 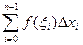есть интегральная сумма, соответствующая некоторому разбиению отрезка 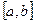и некоторому набору точек 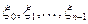отрезка разбиения.

Вычисление определенного интеграла 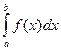геометрически сводится к вычислению площади криволинейной трапеции, ограниченной неотрицательной функцией f(x), осью абсцисс и прямыми 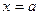и .

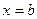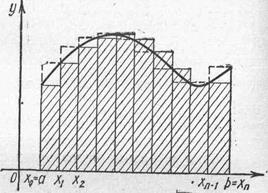
рис. 1.

Для точности численного интегрирования нужно отрезок 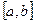разбить на несколько частей и для каждой из них вычислить приближенное значение площади криволинейной трапеции, основанием которой является отрезок 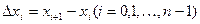, а высотой - число 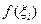, т.е. значение функции в точке

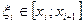, выбранное из условия минимума ошибки интегрирования. Тогда за приближенное значение

интеграла на отрезке 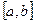принимают интегральную сумму:

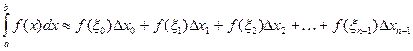
Практически удобно делить отрезок 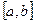на равные части 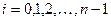, а точки 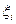совмещать с

левыми 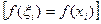или правыми 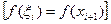концами отрезков разбиения. Если точку 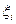совместить с левым концом отрезка 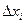, то приближенное значение интеграла геометрически равно площади заштрихованной нижней ступенчатой фигуры и может быть представлено формулой левых прямоугольников:

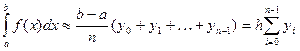(1)

где 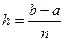- шаг разбиения. Если же в качестве точки 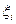. выбрать правый конец отрезка 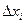, приближенное значение интеграла графически равно площади верхней ступенчатой фигуры, и вычисляется по формуле правых прямоугольников:

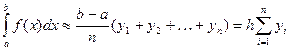(2)

Погрешность вычисления:

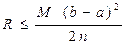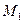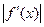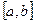, где - максимум на (3)

Пример 1. Используя формулу прямоугольников при 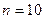, вычислить с тремя десятичными знаками 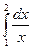. Оценить допущенную погрешность.

Решение: разделим отрезок 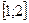на 10 равных частей точками 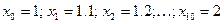и найдём значения функции 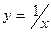в этих точках:

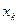	1	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2
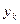	1.000	0.909	0.833	0.769	0.714	0.667	0.625	0.588	0.556	0.526	0.5

Тогда получим 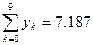и по формуле (1) находим

.

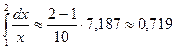Оценим погрешность. Имеем 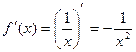; функция 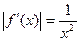монотонно убывает на отрезке 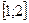, поэтому 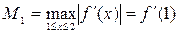и .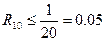

Так как допущенная погрешность влияет уже на второй знак после запятой, то третий знак следует округлить. Значит, 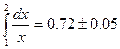. Если вычислить этот интеграл по формуле Ньютона –

Лейбница, то получим 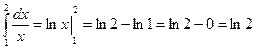. Таким образом, ответ 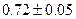является приближённым значением 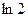. Но 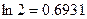; следовательно, при вычислении допущена погрешность, меньшая .

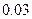Формула трапеций

Приближенное значение определенного интеграла можно вычислить и иным способом.

Заменим на отрезке 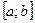дугу АВ графика подынтегральной функции у = f(x) стягивающей ее хордой (рис.2) и вычислим площадь трапеции АВbа. Примем значение определенного

интеграла численно равным площади этой трапеции.

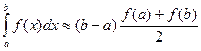(4)

Это и есть формула трапеций для приближенного вычисления интеграла. Погрешность вычисления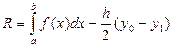

для формулы трапеций оценивается так:

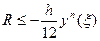, (5)

где точка 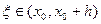. В случае, если 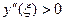, вычисление по формуле (4) даёт значение интеграла с избытком; если 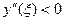, то интеграл вычисляется с недостатком. Точность вычислений возрастает, если отрезок 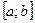разделить на несколько частей и применить формулу трапеций к каждому отрезку 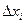(рис. 3). Тогда

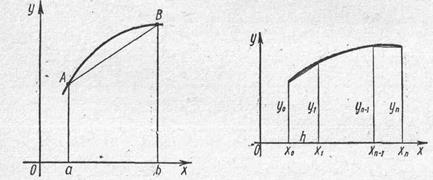
Рис.2 Рис. 3

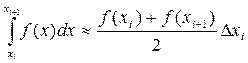
Для простоты вычислений удобно делить отрезок 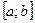на равные части, в этом случае длина каждого из отрезков разбиения есть 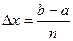. Тогда, численное значение интеграла на всем отрезке 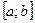равно

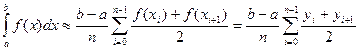
Эта формула называется общей формулой трапеций. Общую формулу трапеций можно переписать в более удобном виде:

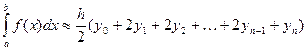, где шаг 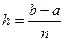(6)

Пример 2.Вычислить интеграл 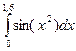с помощью формулы трапеций при .

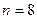Решение: составим таблицу значений подынтегральной функции пр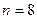и и :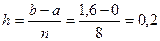

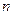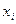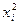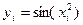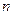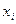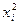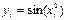	0,2 0,4 0,6	0,02 0,16 0,36	0,0000 0,0400 0,1593 0,3523		0, 1,0 1,2 1,4 1,6	0,64 1,0 1,44 1,96 2,56	0,5972 0,8415 0,9915 0,9249 0,5487

Используя формулу ,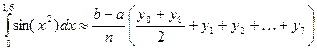

Находим: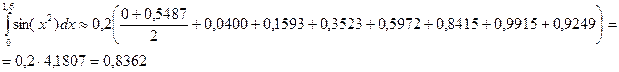

Примечание. Если данный интеграл вычислить при 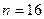, то получим 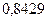. Следовательно, точность вычислений увеличивается с возрастанием .

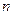Формула Симпсона

Точность приближенного интегрирования заметно возрастает, если подынтегральную функцию 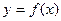на отрезке 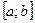заменить квадратичной функцией (рис.5), принимающей в узлах х₀ = а, х₁, х₂ = b значения 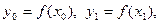и 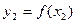. В качестве интерполяционного многочлена используется многочлен Ньютона 2 степени. Тогда

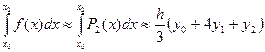(7)

Соотношение (7) называется формулой Симпсона. Формула Симпсона обладает повышенной точностью и является точной не только для многочленов второй степени, но и третьей. Погрешность формулы Симпсона оценивается следующим образом:

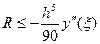,где точка 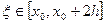(8)

Для увеличения точности вычислений отрезок 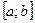разбивают на п пар участков 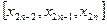(рис. 4) и к каждому из них применяют формулу (7). Тогда численное значение определенного интеграла на всем отрезке 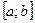будет равно

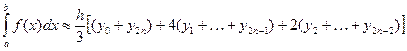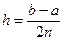, где (9)

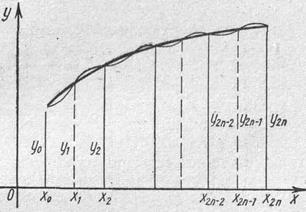
Соотношение (9) называется общей формулой Симпсона.
Пример 3. Вычислить по формуле Симпсона 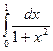при .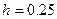

По формуле (9) имеем 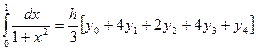. Подставляя в подынтегральную функцию 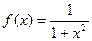значения 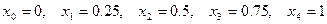, получим

.

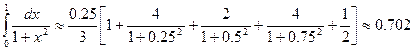Приближенное решение обыкновенных дифференциальных уравнений. Метод Эйлера

Простейшим обыкновенным дифференциальным уравнением является уравнение первого порядка, разрешенное относительно производной:

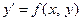(10)

Основная задача, связанная с этим уравнением, известна как задана Коши:найти решение уравнения (10) в виде функции у(х), удовлетворяющей начальному условию

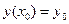(11)

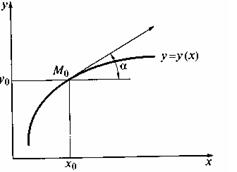
Рис.6

Геометрически это означает, что требуется найти ин­тегральную кривую у = у(х), проходящую через

заданную точку M₀(x₀, .y₀), при выполнении равенства (11) (см. рис.6). С численной точки зрения задача Коши выглядит следующим образом: требуется построить таблицу значений функции у=у(х), удовлетворяющей уравнению (10) и начальному условию (11) на отрезке [a;b]с некоторым шагом h. Обычно считается, что х₀ = а, т.е. начальное условие задано в левом конце отрезка.

Простейшим из численных методов решения дифференциальных уравнений является метод Эйлера.В основе метода Эйлера лежит идея графического постро­ения решения дифференциально­го уравнения, однако этот метод дает одновременно и способ на­хождения искомой функции в численной (табличной) форме.

Пусть дано уравнение (10) с начальным условием (11) (т.е. поставлена задача Коши). Решим вначале следующую задачу: най­ти простейшим способом прибли­женное значение решения в не­которой точке x₁ = х₀ + h, где h - достаточно малый шаг.

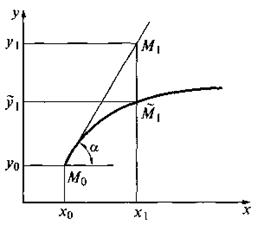
Рис. 7

Заметим, что уравнение (10) совместно с началь­ным условием (11) задают направ­ление касательной к искомой ин­тегральной кривой в точке М₀(х₀, у₀). Уравнение касательной имеет вид

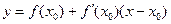(12)

Двигаясь вдоль этой касательной (рис. 7), учитывая соотношения (10) и (12), получим приближенное значение решения в точке х₁:

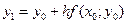(13)

Располагая приближенным ре­шением в точке М₁ (х₁,y₁), можно повторить описанную ранее процедуру: построить прямую, про­ходящую через эту точку с угловым коэффициентом f (х₁, y₁) и по ней найти приближенное значение решения в точке х₂ = х₁ + h. Заметим, что в отличие от ситуации, изображенной на рис. 7, эта прямая не есть касательная к реальной интегральной кривой, поскольку точка M₁, нам недоступна. Однако представляется инту­итивно ясным, что если h достаточно мало, то получаемые при­ближения будут близки к точным значениям решения.

Продолжая эту идею, построим систему равноотстоящих точек

х_i = x₀ + ih ( i = 0, 1, 2, ..., n) (14)

Получение таблицы значений искомой функции у(х) по методу Эйлера заключается в циклическом

применении формулы

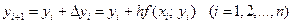, (15)

Геометрическая иллюстрация метода Эйлера приведена на рис. 8. Вместо интегральной кривой в реальности получается сово­купность прямых (так называемая ломаная Эйлера).

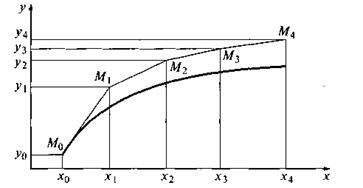
Рис.8 Ломаная Эйлера

Методы численного интегрирования дифференциальных урав­нений, в которых решение получается от одного узла к другому, называются пошаговыми. Метод Эйлера — простейший представи­тель семейства пошаговых методов.

Отметим, что оценка погрешности метода при таком эле­ментарном рассмотрении невозможна даже на первом шаге. Кроме того, особенностью любого пошагового метода является то, что, начиная со второго шага исходное значение у, в формуле (13) само является приближенным, т.е. погрешность на каж­дом следующем шаге систематически возрастает.

Наиболее используемым эмпирическим методом оценки то­чности как метода Эйлера, так и других пошаговых методов при­ближенного численного интегрирования обыкновенных диффе­ренциальных уравнений является способ двойного прохождения заданного отрезка — с шагом h и с шагом h/2. Совпадение соот­ветствующих десятичных знаков в полученных двумя способами результатах дает эмпирические основание считать их верными (хотя полной уверенности в этом быть не может).

Одна из принципиальных трудностей всех пошаговых методов численного решения дифференциальных уравнений состоит в воз­можности столкнуться с неустойчивостью метода. Оценка погреш­ности неявно предполагает, что ломаная приближенного реше­ния (см. рис. 8) хотя и не совпадает с интегральной кривой, но качественно на нее похожа. Чаще всего это именно так, но иногда (например, при неудачном выборе шага h) приближенное реше­ние может быть качественно непохожим на точное (например, точное монотонно убывает, а приближенное монотонно возрас­тает).

Для эмпирического контроля того, не имеет ли места неустой­чивость, следует численно интегрировать уравнение с нескольки­ми, значительно отличающимися, значениями шага h, сравнивая качественно поведение решений.

Пример 4.Применяя метод Эйлера, составить таблицу значений решения дифференциального уравнения 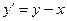, с начальным условием 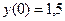на отрезке 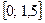, приняв h=0,25. Вычисления проводить с 4-мя знаками после запятой.

Решение:

Для удобства вычислений составим таблицу.

1-й шаг: по начальным условиям заполним первую строку во 2-м и 3-м столбцах ;

2-й шаг: из уравнения 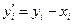вычисляем 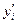( i = 0, 1, 2, 3, 4, 5) в столбце (4);

3-й шаг: содержимое столбца (4) умножаем на h (вычисляем 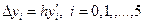) и

записываем результат в столбец (5) этой же строки;

4-й шаг: к содержимом столбца (3) прибавляем содержимое столбца (5) этой же строки

(вычисляем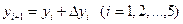и результат записывает столбец (3)следующей

строки. Определяем х_i+1 = x_i + h и затем шаги 2-4 повторяем до тех пор, пока не будет пройден

весь отрезок .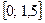

i	xi	yi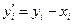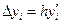
(1)	(2)	(3)	(4)	(5)
		1,5000	1,5000	0,3750
	0,25	1,8750	1,6250	0,4062
	0,50	2,2812	1,7812	0,4453
	0,75	2,7265	1,9765	0,4951
	1,00	3,2206	2,2206	0,5552
	1,25	3,7758	2,5258	0,6314
	1,50	4,4072

Пример 5. Решить методом Эйлера дифференциальное урав­нение 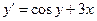с начальным значением у(0) = 1,3 на отрез­ке [0; 1], приняв шаг h = 0,2.

Решение: результаты вычислений с двумя знаками после запятой приве­дены в таблице:

i	xi	yi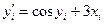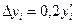
(1)	(2)	(3)	(4)	(5)
	0,0	1,3	0,27	0,05
	0,2	1,35	0,82	0,16
	0,4	1,51	1,25	0,25
	0,6	1,76	1,61	0,32
	0,8	2,08	1,91	0,38
	1,0	2,46

Задание

Вариант 1

1.По формуле левых прямоугольников для n=12 вычислить значение интеграла: .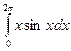

2. По формуле трапеций n=10 вычислить значение интеграла с тремя десятичными

знаками: .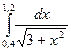

3. По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными

знаками: .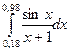

4. Применяя методом Эйлера, составить таблицу значений решения дифференциального урав­нения

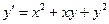с начальным условием у(2) = 1, 2 на отрез­ке [2; 3], приняв шаг h = 0,1.

Сделайте ручную прикидку графика интегральной кривой на бумаге.

Вариант 2

1.По формуле левых прямоугольников для n=12 вычислить значение интеграла: .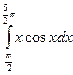

2.По формуле трапеций n=8 вычислить значение интеграла с тремя десятичными

знаками: .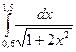

3.По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными

знаками: .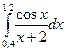

4. Применяя методом Эйлера, составить таблицу значений решения дифференциального урав­нения

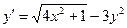с начальным условием у(2,6) = 1, 8 на отрез­ке [2,6; 4,6], приняв шаг h = 0,2.

Сделайте ручную прикидку графика интегральной кривой на бумаге.

Вариант 3

1.По формуле правых прямоугольников для n=12 вычислить значение интеграла:

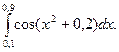
2.По формуле трапеций для n=10 вычислить значение интеграла с тремя десятичными

знаками: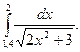

3. По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными

знаками: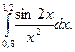

4. Применяя методом Эйлера, составить таблицу значений решения дифференциального урав­нения

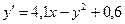с начальным условием у(0,6) = 3,4 на отрез­ке [0,6; 2,6], приняв шаг h = 0,2.

Сделайте ручную прикидку графика интегральной кривой на бумаге.

Вариант 4

1.По формуле правых прямоугольников для n=12 вычислить значение интеграла:

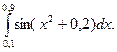
2. По формуле трапеций для n=10 вычислить значение интеграла с тремя десятичными знаками: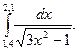

3. По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными

знаками: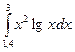

4. Применяя методом Эйлера, составить таблицу значений решения дифференциального урав­нения

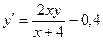с начальным условием у(3) = 1,7 на отрез­ке [3; 5], приняв шаг h = 0,2.

Сделайте ручную прикидку графика интегральной кривой на бумаге.

4. Контрольные вопросы:

1. Какие методы приближенного вычисления определенных интегралов вы знаете? Назовите

формулы для вычислений. Какой из них дает наиболее точный результат?

2. На чем основан метод Эйлера приближенно решения дифференциальных уравнений?

5. Содержание отчёта:

5.1 Наименование работы

5.2 Цель работы

5.3 Задание

5.4 Формулы для расчета

5.5 Необходимые расчеты. Анализ результатов расчетов

5.6 Выводы по работе

5.7 Ответы на контрольные вопросы

Литература:

1. Колягин Ю.М. , Луканкин Г.Л., Яковлев Г.Н. Математика в 2-х томах Учебное пособие - М.

Новая волна, 2005, ч.1, с.565-571;

2. Богомолов Н.В. «Практические занятия по математике» - Учебное пособие – М.:Высш. школа,

2003, с. 211-212;

3. Лапчик М.П., Рагулина М.И., Хеннер Е.К. Элементы численных методов: учебник для студ. сред.

проф. образования -М.: Издательский центр «Академия», 2007, с.152-184