Классическая статистическая физика

Вопросы коллоквиума

1. Фазовое пространство для идеального газа. Микросостояние и макросостояние. Фазовый ансамбль. Число степеней свободы. Число микросостояний. Плотность микросостояний фазового ансамбля. Теорема Лиувилля.

2. Каноническое распределение. Условие применимости. Статистический интеграл. Свободная энергия. Применение к идеальному газу. Статистический интеграл поступательного движения частицы.

3. Распределение энергии частицы по степеням свободы для гамильтониана со степенными зависимостями. Неустранимая погрешность измерительного прибора с упругой силой.

4. Распределение Максвелла по модулю скорости и по энергии для концентрации частиц. Наиболее вероятные и средние значения.

5. Распределение Больцмана по координатам для концентрации частиц. Формула Больцмана для однородного поля тяжести.

6. Термодинамические потенциалы. Внутренняя энергия. Химический и электрохимический потенциал. Условие равновесия системы. Химический потенциал и статистический интеграл. Зависимости химического потенциала.

КЛАССИЧЕСКАЯ СТАТИСТИЧЕСКАЯ ФИЗИКА

Основные положения

Изучаемая система – идеальный газ частиц, подчиняющихся классической механике.

Микросостояние системы – совокупность координат и импульсов всех частиц, зафиксированных в один момент времени. Отображается точкой X фазового пространства. Возможность тех или иных микросостояний определяет функция распределения 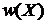в фазовом пространстве и статистический интеграл Z– нормировочная постоянная распределения.

Макросостояние системы – состояние газа как единого целого. Описывается термодинамическими величинами – температурой Т, давлением Р, внутренней энергией U, свободной энергией F и др. Термодинамические характеристики являются средними по распределению и получаются на основе Z.

Фазовое пространство системы частиц

Микросостояние системыотображается точкой фазового пространства

,

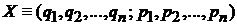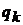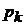где и – обобщенные координаты и импульсы частиц системы. С течением времени точка X движется согласно уравнениям Гамильтона

,

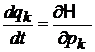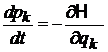. (2.1)

Гамильтониан 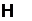– полная энергия системы, выраженная через координаты и импульсы частиц

.

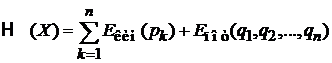Для нерелятивистской классической частицы массой m, движущейся вдоль оси k с импульсом 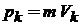, кинетическая энергия

.

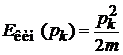Для консервативной системы полная энергия сохраняется

,

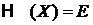и все микросостояния находятся на гиперповерхности в фазовом пространстве.

Найдем число измерений фазового пространства.

Число степеней свободы системы

Если число степеней свободы частицы f, то для N независимых частиц число степеней свободы:

,

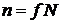и размерность фазового пространства системы .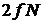

Число микросостояний

Элемент объема фазового пространства для системы с числом частиц N

.

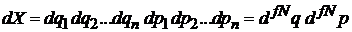При 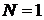, , 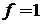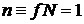единица измерения

,

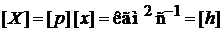где h – постоянная Планка.

При 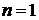соотношение неопределенностей Гейзенберга

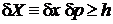
ограничивает снизу фазовый объем микросостояния величиной h. В 2n-мерном фазовом пространстве объем одного микросостояния 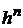. В результате число микросостояний равно безразмерному фазовому объему системы

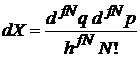. (2.2)

Множитель N! учитывает тождественность микрочастиц – их взаимная перестановка дает N! точек фазового пространства, отвечающих одному и тому же состоянию, которое должно учитываться однократно.

Вычисление объема

Идеальный свободный классический газ имеет 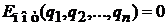и полную энергию

,

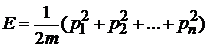тогда

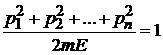
является уравнением сферы. Микросостояния с энергией Е находятся в импульсном пространстве на сфере радиусом .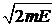

Объем и площадь n-мерной сферы

На основании размерности для объема n-мерной сферы получаем

,

.

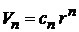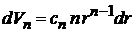Находим 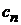, вычисляя по всему пространству интеграл:

.

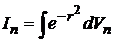В декартовых координатах

, ,

,

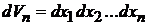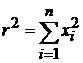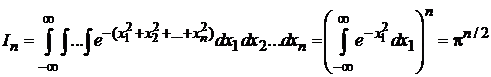где использован интеграл Пуассона

.

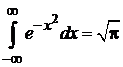В сферических координатах

,

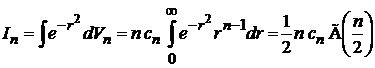где использовано

,

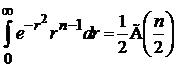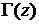– гамма-функция.

Сравнение выражений для 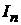дает

.

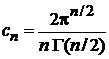Объем шара и шарового слоя

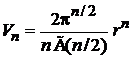, (П.2.1)

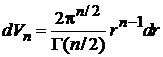. (П.2.2)

Площадь сферы

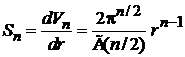, (П.2.3)

где

Г(n + 1) = n!,

Г(z + 1) = z Г(z),

,

, , ,

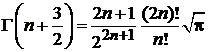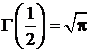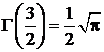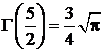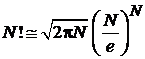, где .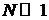

Для эллипсоида с полуосями 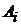уравнение

,

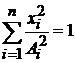объем

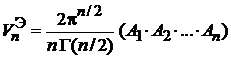. (П.2.1а)

Фазовая траектория

С течением времени система изменяет свое микросостояние за счет движения частиц, и точка X перемещается по фазовой траектории согласно уравнениям Гамильтона (2.1)

,

.

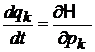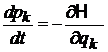Условие нормировки

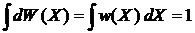. (2.4)

Теорема Лиувилля

Идеальный газ описывается гамильтонианом .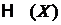

Фиксируем макросостояние, т. е. термодинамические параметры. Макросостояние реализуется ансамблем микросостояний. В фазовом пространстве они отображаются множеством точек, которые передвигаются с течением времени.

Теорема Лиувилля утверждает – движение точек фазового ансамбля подобно течению несжимаемой жидкости, сохраняющей свой объем и плотность. Плотность микросостояний зависит от гамильтониана и не изменяется с течением времени.

Следствия теоремы

А. Согласно теореме число микросостояний ансамбля и плотность микросостояний сохраняются, тогда фазовый объем элемента ансамбля не изменяется с течением времени

,

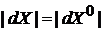изменяется лишь форма объема. Учитываем

,

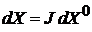где J – якобиан преобразования между начальными и текущими координатами. Тогда

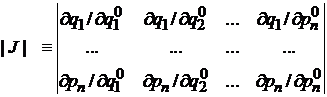= 1.

Модуль якобиана, связывающего начальные и текущие фазовые координаты, равен единице.

Б. Проекция фазового объема на любую координатную плоскость независима от других. Фазовый объем не изменяется, тогда площадь каждой проекции постоянна. Для одной частицы в проекции на плоскость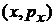

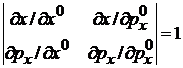. (2.5)

В. Для стационарной системы функция распределения не изменяется с течением времени и может зависеть только от интегралов движения. Если система как целое неподвижна и не вращается, то функция распределения зависит от полной энергии, т. е. от гамильтониана:

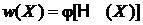. (2.6)

Г. Для равновесной консервативной системы

.

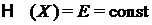Система с равной вероятностью обнаруживается в любом из доступных микросостояний.

Д. Теорема не выполняется для диссипативных систем, т. е. при наличии трения, неупругих соударений, когда уравнения Гамильтона (2.1) неприменимы.

ПРИМЕР

Одномерный гармонический осциллятор (двухатомная молекула с упругой связью, матический маятник, шарик на пружине, и т. д.) колеблется с частотой ω и имеет энергию E. Найти фазовую траекторию. Проверить выполнение теоремы Лиувилля.

1. Если энергия системы фиксирована, то микросостояния в фазовом пространстве движутся по гиперповерхности. Для одномерной системы из одной частицы координаты фазового пространства (x,p). Гамильтониан осциллятора приравниваем полной энергии

.

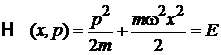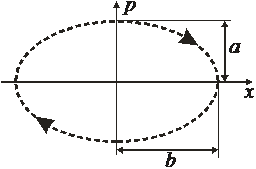
2. Получаем уравнение фазовой траектории, по которой двигаются микросостояния:

.

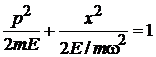Микросостояния отличаются начальной фазой. Сравниваем с уравнением эллипса на плоскости (y,z)

,

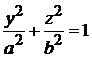находим полуоси вдоль p и x

, .

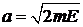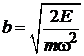3. Число микросостояний

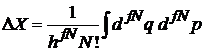. (2.3б)

При 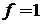, 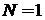интеграл равен площади эллипса

,

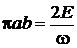тогда

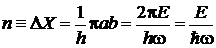, (П.2.4)

где 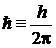. Следовательно, энергия осциллятора квантуется

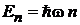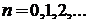, , (П.2.4а)

спектр эквидистантный. Горизонтальная линия на рис. соответствует состоянию с определенной энергией. 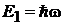– интервал эквидистантного спектра осциллятора.

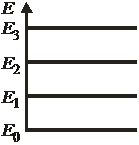
4. Для получения якобиана

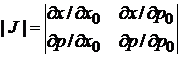
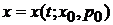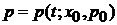необходимо найти и , где 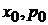– начальные координата и импульс, т. е. при .

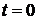Используем уравнения Гамильтона

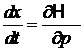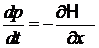, . (2.1)

Подставляем гамильтониан осциллятора

,

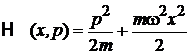получаем

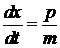– связь скорости с импульсом,

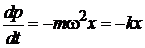– 2-й закон Ньютона ,

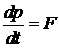где 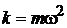– коэффициент жесткости упругой силы F;

.

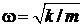Дифференцируем первое уравнение

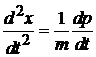
и подставляем второе

.

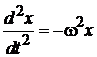Общее решение

,

.

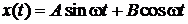Начальные значения

,

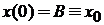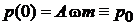
дают

, ,

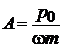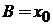тогда координаты микросостояния

,

.

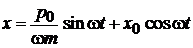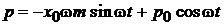С течением времени микросостояние движется по эллипсу по часовой стрелке.

5. Вычисляем якобиан

.

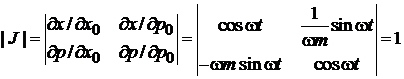Теорема Лиувилля выполняется.

Нормировочная постоянная

В выражение

(2.8)

подставляем

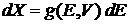, (2.9)

­получаем

.

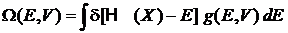Фильтрующее свойство дельта-функции снимает интеграл и дает

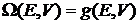. (2.10)

Нормировочная постоянная микроканонического распределения равна энергетической плотности состояний.

ПРИМЕР 1

Атом массой m с энергией e находится в объеме V, где все точки и направления равноправны. Найти энергетическую плотность состояний. Получить температуру и давление, создаваемые фазовым ансамблем. Рассмотреть случай, когда в объеме находятся N атомов идеального газа.

Энергия и импульс атома связаны соотношением

.

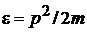Фазовый ансамбль находится в импульсном пространстве на сфере радиусом

.

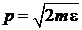Микросостояния фазового ансамбля отличаются направлениями вектора импульса. Число микросостояний, или фазовый объем

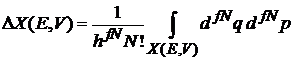
при ,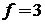

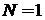
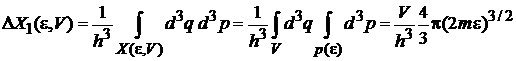. (2.2а)

Учтена независимость импульса от координат при отсутствии внешнего поля. Из

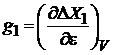(2.9а)

получаем

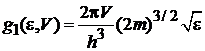. (П.2.5)

Плотность состояний классического газа пропорциональна корню квадратному из энергии.

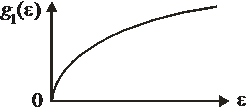
Из

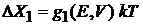(2.14)

находим

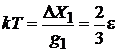. (П.2.6)

Температура пропорциональна энергии частицы.

При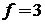

,

.

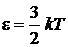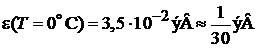Из

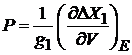, (2.12)

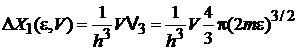, (2.2а)

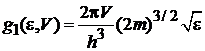, (П.2.5)

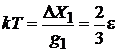, (П.2.6)

получаем давление, создаваемой фазовым ансамблем, соответствующим одной частице:

.

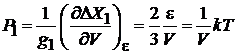Получили уравнение идеального газа 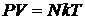для одной частицы.

Азот N₂:

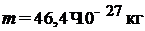
при

, ,

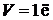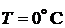имеет

, .

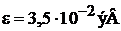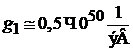На интервале энергии 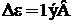находятся 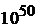уровней, следовательно, классический газ имеет квазинепрерывный спектр.

Для N частиц с полной энергией E

.

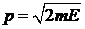Для объема импульсного пространства в виде шара размерностью 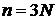используем

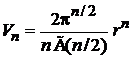, (П.2.1)

получаем

,

,

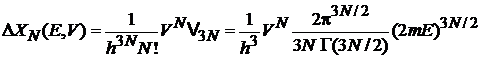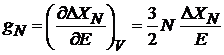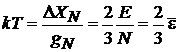
– температура пропорциональна средней энергии частицы.

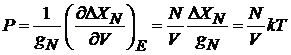
– уравнение идеального газа .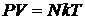

ПРИМЕР 2

Система из N одномерных гармонических осцилляторов с полной энергией Е. Найти энергетическую плотность состояний и среднюю энергию осциллятора.

Полная энергия системы

,

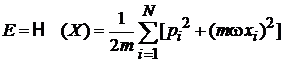тогда

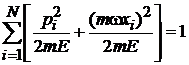
– уравнение эллипсоида в 2N-мерном пространстве,

N полуосей – ,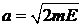

N полуосей – ,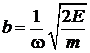

.

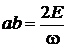Фазовый объем системы пропорционален объему эллипсоида

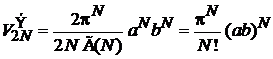. (П.2.1а)

Число микросостояний

,

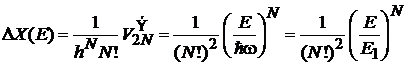где 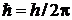; 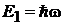– интервал эквидистантного спектра осциллятора.

Из

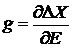(2.9а)

получаем энергетическую плотность состояний

.

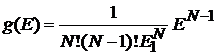Из

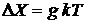(2.14)

находим

.

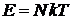Средняя энергия осциллятора

.

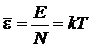Каноническое распределение

Объект – равновесный идеальный газ из N частиц в объеме V в термостате с температурой Т.

По фазовому пространству

Идеальный газ – любые подсистемы независимы, энергия их взаимодействия друг с другом равна нулю.

Систему делим на подсистемы 1 и 2, тогда

.

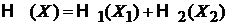По теореме Лиувилля распределения для подсистем и для всей системы выражаются через соответствующие гамильтонианы

,

,

.

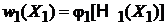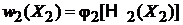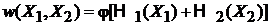По теореме об умножении вероятностей независимых событий распределения связаны между собой

,

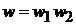тогда

.

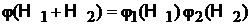Логарифмируем

,

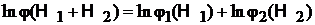берем дифференциал

,

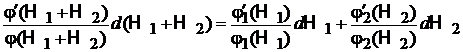где .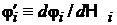

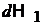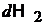Учитываем, что и – независимые величины, тогда

.

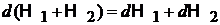В результате получаем

,

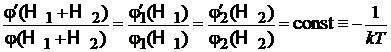k – постоянная Больцмана, смысл T устанавливается далее. Следовательно:

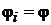– универсальная функция,

.

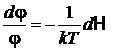Интегрируем

.

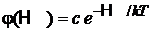Полагаем 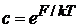, как показано далее 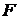– свободная энергия системы.

Получаем каноническое распределение

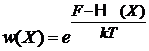(2.15)

– вероятность обнаружения микросостояния в единице объема фазового пространства около точкиX,

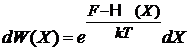(2.15а)

– вероятность обнаружения микросостояния в объеме dX фазового пространства около точкиX.

Статистический интеграл системыZ

Полагаем ,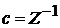

,

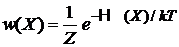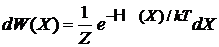. (2.16)

Условие нормировки

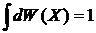
дает макрохарактеристику – статистический интеграл системы

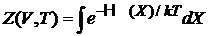. (2.17)

Статистический интеграл частицы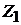

Для идеального газа из N тождественных частиц

,

,

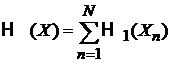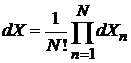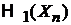– гамильтониан частицы n.

С учетом 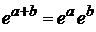интеграл (2.17) распадается на произведение N одинаковых интегралов. Получаем выражение стат. интеграла системы через стат. интеграл одной частицы

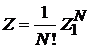, (2.18)

где макрохарактеристика – статистический интеграл частицы

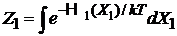, (2.19)

.

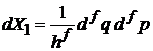Для независимых видов движения частицы: поступательного, вращательного, колебательного и внутреннего

H₁ = (H_пост)₁ + (H_вращ)₁ + (H_колеб)₁+ (H_внутр)₁,

тогда

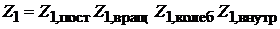. (2.20)

Для N частиц

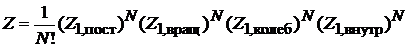. (2.21)

Далее получено

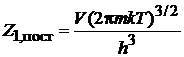, (2.22)

для двухатомной молекулы с моментом инерции J и частотой собственных колебаний w

,

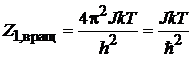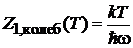. (2.23)

Физический смыслT

Общее начало термодинамики –если температуры систем одинаковые, то тепловой контакт не изменяет их макросостояний.

До контакта

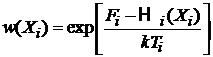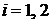, . (2.16)

В момент контакта в силу независимости систем их общее распределение

.

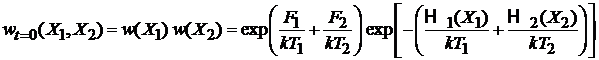С течением времени гамильтонианы изменяются, их сумма сохраняется. Распределение не меняется, если 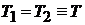. Следовательно, Т – температура.

Смысл свободной энергии

Является термодинамическим потенциалом – не зависит от пути перехода между начальным и конечным состояниями.

Является полным дифференциалом своих аргументов

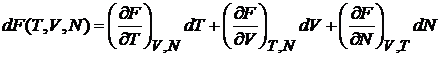. (2.30а)

В термодинамике известно соотношение

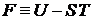. (2.31)

Берем дифференциал

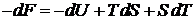. (2.31а)

Для равновесного, обратимого процесса используем

,

,

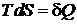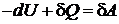тогда

,

и из (2.31а) при 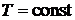получаем

.

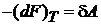Следовательно, свободная энергия является частью внутренней энергии, которая при изотермическом процессе переходит в работу.

Связанная энергия

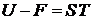
– часть внутренней энергии, которая при изотермическом процессе не может быть превращена в работу и выделяется в виде теплоты.

Понятия свободной и связанной энергий ввел Герман Гельмгольц в 1847 г.

ПРИМЕР 1

N атомов идеального газа в объеме V при температуре Т совершают поступательные движения. Найти статистический интеграл, внутреннюю энергию и давление.

1. Статистический интегралатомов

Используем

,

.

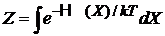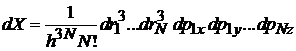Атомы совершают поступательные движения, тогда гамильтониан

.

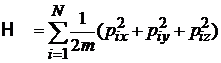Подстановка дает

,

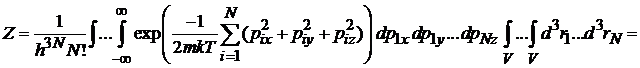
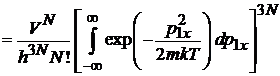где учтено

.

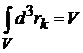Согласно

,

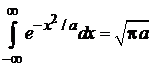интеграл в квадратных скобках равен 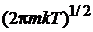. В результате статистический интеграл поступательного движения

,

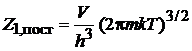. (П.3.1)

2. Внутренняя энергия

Используем

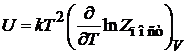. (2.26)

Из (П.3.1)

.

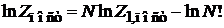По формуле Стирлинга

, ,

,

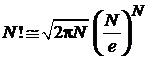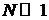тогда

.

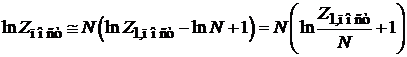С учетом (П.3.1)

,

получаем

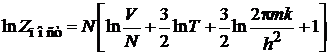. (П.3.1а)

Из

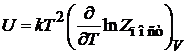(2.26)

получаем

,

.

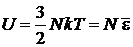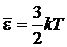3. Давление

Из (2.34) и (П.3.1а)

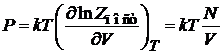
находим

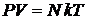– уравнение идеального газа,

, , .

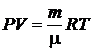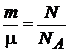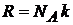ПРИМЕР 2

В двухатомной молекуле при температуре Т атомы совершают колебания с частотой ω. Найти статистический интеграл колебаний.

Молекулу считаем линейным осциллятором с гамильтонианом

.

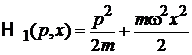Из

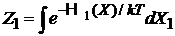, (2.17)

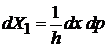
находим

.

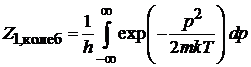
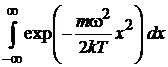Используя интеграл Пуассона

,

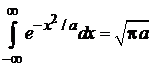для интегралов получаем

, .

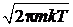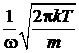В результате статистический интеграл колебательного движения молекулы

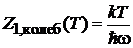. (П.3.5)

ПРИМЕР 3

Молекула массой m состоит из двух одинаковых атомов, находящихся на расстоянии 2r и вращающихся благодаря температуре Т. Найти статистический интеграл вращений.

Используем сферические координаты с центром в точке симметрии молекулы. На рисунке жирный круг – атом, второй атом в симметричной точке не показан.

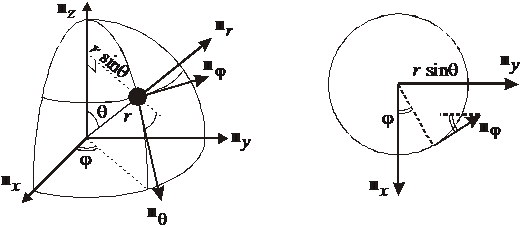
Атом вращается, изменяются углы φ и θ, угловая скорость связана с линейной скоростью

.

Линейную скорость атома разлагаем на составляющие:

· вдоль 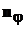со скоростью , где .

· вдоль 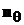со скоростью 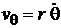, где .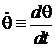

Кинетическая энергия двух атомов, выраженная через обобщенные координаты (φ, θ) и скорости 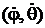, называется функцией Лагранжа

,

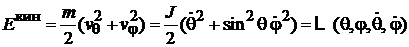где

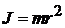
– момент инерции молекулы относительно прямой, перпендикулярной к оси молекулы и проходящей через центр масс.

Гамильтониан выражается через обобщенные импульсы 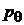и . Находим их из уравнения Лагранжа

.

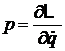Получаем

,

.

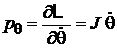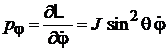Тогда

, .

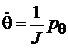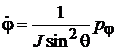Из

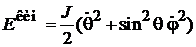
находим гамильтониан пространственного вращения

.

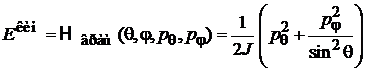Результат подставляем в

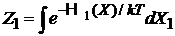, (2.17)

где

.

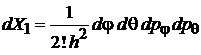Находим

.

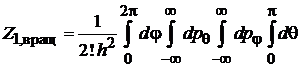
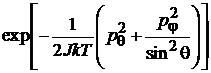Интегрируем вначале по j, затем по p_q, p_j и по θ.

С учетом

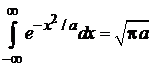
получаем

,

.

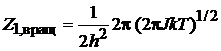
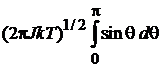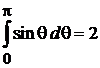Статистический интеграл вращательного движениямолекулы

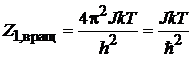. (П.3.6)

По степеням свободы

Если степени свободы частицы входят в гамильтониан симметрично, то на каждую степень свободы приходится одинаковая тепловая энергия, обусловленная температурой.

Теорему предложил Дж. Уотерстон в 1845 г.,

количественное выражение дали Джемс Клерк Максвелл в 1860 г. и Людвиг Больцман в 1868 г.

Теорема применима для классических систем. Для квантовых систем теорема не выполняется.

Гамильтониан частицы

Рассмотрим гамильтониан со степенными зависимостями от координат и импульсов

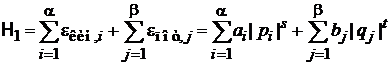, (2.38)

a – число активизированных степеней свободы кинетической энергии;

b – число активизированных степеней свободы потенциальной энергии;

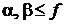– число степеней свободы частицы.

Средние значения

Примеры

1. Нерелятивистская свободная частица

, .

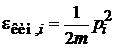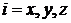Сравниваем с

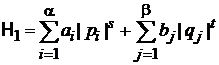, (2.38)

в виде

,

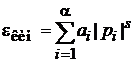находим

, ,

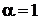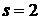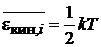. (2.40)

Для классического равновесного газа на каждую поступательную степень свободы частицы приходится тепловая кинетическая энергия .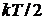

2. Линейный гармонический осциллятор

.

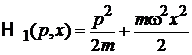Сравниваем с

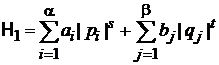, (2.38),

получаем

, ,

,

,

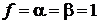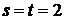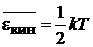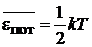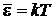
– на гармоническое колебательное движение приходится тепловая энергия kT.

НЕУСТРАНИМАЯ ПОГРЕШНОСТЬ

ИЗМЕРИТЕЛЬНОГО ПРИБОРА

Макрохарактеристики равновесной системы постоянны только в среднем. Колебания – флуктуации – вызваны хаотическими тепловыми движениями молекул.

Измерительное устройство испытывает тепловые колебания. Невозможно измерить физическую величину с точностью, меньшей амплитуды колебаний указателя прибора.

Оценим неустранимую погрешность прибора на примере весов, используя теорему о распределении энергии по степеням свободы.

Весы на основе упругой силы

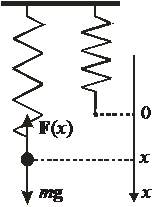
Весы – одномерная система. Потенциальная энергия

,

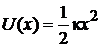x – отклонение указателя от положения равновесия ;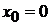

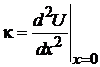– коэффициент жесткости.